
- •«Физические основы электронной техники. Квантовая механика»
- •Векторная модель атома
- •Сложение моментов количества движения в общем случае
- •Сложение спиновых моментов
- •Возможные типы связи в атоме
- •Полный магнитный момент атома. Множитель Ланде1
- •Релятивистская поправка к энергетическим уровням
- •Спин-орбитальное взаимодействие
Спин-орбитальное взаимодействие
Наличие
спина у электрона должно влиять на его
энергию в атоме. Движение электрона
создает магнитное поле, а поскольку
электрон имеет собственный магнитный
момент
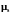 (спиновый), то возникает энергия
взаимодействия магнитного момента с
магнитным полем. Эту энергию необходимо
прибавить к той, которую мы рассматривали
до сих пор.
(спиновый), то возникает энергия
взаимодействия магнитного момента с
магнитным полем. Эту энергию необходимо
прибавить к той, которую мы рассматривали
до сих пор.
Чтобы
определить дополнительную энергию
электрона, обусловленную взаимодействием
спинового магнитного момента электрона
с магнитным полем, перейдем к системе
отсчета, которая движется вместе с
электроном. В этой системе координат
электрон находится в покое в начале
координат, а ядро движется вокруг
электрона со скоростью
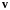 ,
которая численно равняется скорости
электрона, но имеет противоположное
направление. При своем движении
положительно заряженное ядро создает
ток силой
,
которая численно равняется скорости
электрона, но имеет противоположное
направление. При своем движении
положительно заряженное ядро создает
ток силой
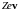 ,
а магнитное поле этого тока в точке, где
находится электрон, будет равняться
,
а магнитное поле этого тока в точке, где
находится электрон, будет равняться
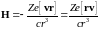 .
(6.44)
.
(6.44)
Векторное произведение представим с помощью момента количества движения электрона. Принимая во внимание, что орбитальный момент
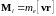 ,
(6.45)
,
(6.45)
получим
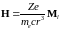 . (6.46)
. (6.46)
Дополнительную
энергию взаимодействия спинового
магнитного момента электрона
с магнитным полем
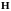 можно рассматривать как малое возмущение
по сравнению с главной частью гамильтоновой
функции
можно рассматривать как малое возмущение
по сравнению с главной частью гамильтоновой
функции

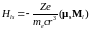 .
(6.47)
.
(6.47)
В соответствии с выводами теории возмущения (см. разд. 5.1) дополнительная энергия, которая обусловлена возмущением, равняется среднему значению оператора возмущения в соответствующем невозмущенном состоянии, то есть
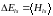 .
(6.48)
.
(6.48)
Ввиду
того, что в (6.47) изменяется только
 ,
усреднять нужно только
,
усреднять нужно только
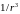 :
:
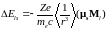 .
(6.49)
.
(6.49)
Поскольку
усреднение проводится по невозмущенными
состояниями, можно воспользоваться
собственными функциями для атома
водорода или водородоподобных ионов
(см. табл.2.1, необходимо учитывать заряд
ядра
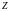 ).
В результате вычисления получим
).
В результате вычисления получим
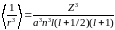 ,
(6.50)
,
(6.50)
где
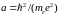 –
боровский радиус.
–
боровский радиус.
Рассмотрим
теперь скалярное произведение
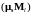 .
Спиновый магнитный момент электрона
связан со спином соотношением (3.20), а
численные значения спинового и
орбитального моментов равняются
.
Спиновый магнитный момент электрона
связан со спином соотношением (3.20), а
численные значения спинового и
орбитального моментов равняются
 ,
(6.51)
,
(6.51)
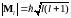 .
(6.52)
.
(6.52)
Следовательно,
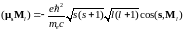 .
(6.53)
.
(6.53)
Подставляем (6.50) и (6.53) в (6.49) и получим
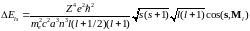 .
(6.54)
.
(6.54)
Но
учет всех релятивистских эффектов
уменьшает это выражение вдвое.
Воспользовавшись боровским радиусом
,
постоянной Ридберга
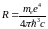 ,
постоянной Планка
,
постоянной Планка
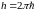 и постоянной тонкой структуры
и постоянной тонкой структуры
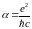 ,
получим из (6.54):
,
получим из (6.54):
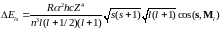 .
(6.55)
.
(6.55)
Вычислим, воспользовавшись рис.6.1 и теоремой косинусов
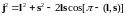 ,
,
где
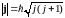 ,
,
 ,
.
Отсюда находим
,
.
Отсюда находим
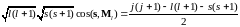 .
(6.56)
.
(6.56)
Подставим (6.56) в (6.55) и получим
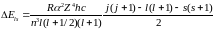 ,
,
а отсюда поправка к терму (2.70):
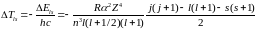 .
(6.57)
.
(6.57)
Поскольку
для электрона
 ,
то второй множитель в формуле принимает
значение:
,
то второй множитель в формуле принимает
значение:
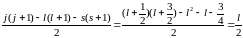 для
для
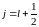
и
 для
для
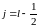 .
.
Соответствующие
значения
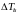 будут
будут
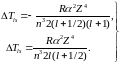 (6.58)
(6.58)
Таким
образом, полная поправка
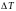 к
терму состоит из суммы релятивистской
поправки
к
терму состоит из суммы релятивистской
поправки
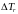 и
поправки спин-орбитального взаимодействия
и
поправки спин-орбитального взаимодействия
 .
.
Воспользовавшись формулами (6.55) и (6.58) и выполнив ряд несложных преобразований, получим формулу тонкой структуры
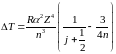 ,
(6.59)
,
(6.59)
где
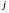 –
квантовое число:
.
–
квантовое число:
.
Из
формулы видно, что для термов
 ,
для которых
принимает
только одно значение 1/2, поправка лишь
смещает
,
для которых
принимает
только одно значение 1/2, поправка лишь
смещает
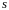 -термы,
но не расщепляет их. Для остальных термов
(
-термы,
но не расщепляет их. Для остальных термов
(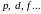 )
квантовое число
принимает
по два значения
)
квантовое число
принимает
по два значения
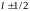 ,
поэтому каждый уровень, который отвечает
этим термам, расщепляется на два
подуровня. Например, для главного
квантового числа
,
поэтому каждый уровень, который отвечает
этим термам, расщепляется на два
подуровня. Например, для главного
квантового числа
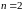 расщепление дает три подуровня (один
расщепление дает три подуровня (один
 -терм
и два
-терм
и два
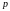 -терма), для
-терма), для
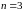 пять подуровней и т.д. однако среди этих
подуровней всегда находятся попарно
совпадающие. Поэтому для
образуется только два подуровня вместо
трех, для
– три подуровня вместо пяти и т.д. Кроме
того, следует принять во
внимание,
что в соответствии с формулой (6.59)
поправка
быстро
уменьшается при увеличении главного
квантового числа
пять подуровней и т.д. однако среди этих
подуровней всегда находятся попарно
совпадающие. Поэтому для
образуется только два подуровня вместо
трех, для
– три подуровня вместо пяти и т.д. Кроме
того, следует принять во
внимание,
что в соответствии с формулой (6.59)
поправка
быстро
уменьшается при увеличении главного
квантового числа
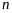 .
Поэтому тонкая структура линий серии
Бальмера определяется двойственностью
уровня
.
.
Поэтому тонкая структура линий серии
Бальмера определяется двойственностью
уровня
.
1 Ланде Альфред (1888-1975) – немецкий физик-теоретик. Работы по изучению атомной структуры, атомных спектров, термодинамике, квантовой механике. Им введен g–фактор.
