Релятивистская поправка к энергетическим уровням
Задача о движении электрона в поле центральной силы, которую мы рассмотрели в розд.2, наиболее корректно развязывается с помощью уравнения Дирака (ф-ла 3.12). При этом решение автоматически учитывает релятивистскую зависимость массы электрона от скорости, а также наличие спину и его взаимодействие с орбитальным моментом.
Поскольку мы не решаем уравнения Дирака, мы воспользуемся уравнением Шредингера, в котором учтем поправку на зависимость массы от скорости. Чтобы получить релятивистское волновое уравнение для движения в центральном поле, запишем релятивистский гамильтониан, а затем заменим величины, которые входят в него, на соответствующие операторы, как это мы делали раньше. Релятивистский гамильтониан
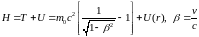. (6.32)
Определим
.
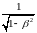Для этого запишем
:
,
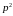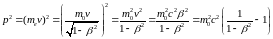откуда
.
Подставим это выражение в (6.5.1):
.
(6.33)
Мы сбережем в (6.33) третий член, а дальнейшими членами пренебрегаем. Третий член мал по сравнению со вторым, поэтому мы можем рассматривать его как возмущение. Следовательно, соответствующее гамильтониану (6.33) волновое уравнение будет иметь вид
.
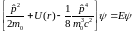(6.34)
Если в (6.34) пренебречь третьим членом, то получим нерелятивистское уравнение Шредингера
.
(6.35)
Допуская, что собственные функции и собственные значения уравнения (6.34) мало отличаются от таковых в нерелятивистском уравнении (6.35), можно считать, что
.
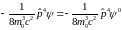Из
уравнения (6.35) имеем
.
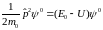Применив еще раз оператор
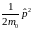и разделив на
,
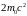получим
,
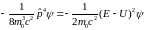(6.36)
где
заменили
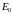на
(в этом приближения это можно делать).
Подставляем (6.36) в (6.34) и получим следующее
уравнение
.
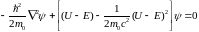(6.37)
Рассмотрим
движение электрона в кулоновском поле
.
Обозначив
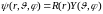и
воспользовавшись результатами разд.
2.1, получим следующее уравнение для
радиальной волновой функции
:
,
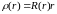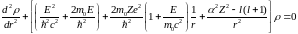(6.38)
где
–
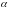постоянная тонкой структуры:
.
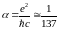(6.39)
Структура
уравнения (6.38) такая же, как и уравнения
Шредингера для радиальной части (2.38).
Поэтому решение проводится таким же
образом, как в разд. 2.2. Сходящееся решение
для
в
виде полинома степени
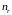получим
только в том случае, когда энергия
принимает определенные значения:
.
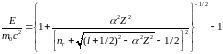(6.40)
Раскладывая
правую часть (6.40) по степеням
,
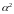получим с точностью до
:
,
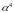(6.41)
где
использовано квантовое число
.
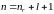Принимая во внимание постоянную Ридберга
и
постоянную тонкой структуры
,
для термов находим
.
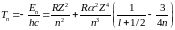(6.42)
Первый член этой формулы есть обычный терм водородоподобного иона, а второй представляет собой искомую релятивистскую поправку
.
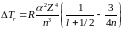(6.43)
В
формулу входит азимутальное квантовое
число
,
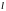следовательно, для разных
поправка
принимает различные значения, и это
приводит к тому, что так называемое
случайное вырождение снимается: термы
для
одного и того же главного квантового
числа
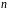будут
иметь различные значения.