
Диференціальні рівняння 1
Диференціальні рівняння – рівність, яка містить незалежну змінну x, невідому функцію y та y’..y(n).
F(x,y,y’..y(n))
Порядок старшої похідної називається порядком даного рівняння.
Якщо невідома функція залежить від кількох змінних, то диференціальне рівняння називають диференціальним в частинних похідних, а якщо невідома функція залежить тільки від однієї змінної – звичайне диференціальне рівняння.
В теоріі диференціальних рівнянь в основному розглядаються диференціальні рівняння, що розв’язні відносно старшої похідної: y(n)=f(x,y,y’..y(n-1)). (1)
Функція y, що має неперервні похідні до n-го порядку включно, перетворює рівняння в тотожність – розв’язок рівняння. Графіком називають інтегральною кривою. Важливу роль в теоріі диференціальних рівнянь відіграє задача, яка полягає в знаходженні такого y=y(x), що задовільняє y(x0)=y0,y’(x0)=y’0, y(n-1)(x0)=y(n-1)0.
Перелічені умови називають початковими. n=1, y(x0)=y0 – означає, що серед усіх розв’язків диференціальних рівнянь треба знайти саме той розв’язок, графік якого проходить через точку (x0,y0).
Якщо розв’язок одержано у вигляді співвідношення φ(x,y)=0 (не розв’язане відносно y), таке співвідношення називають інтегралом (першим) диференціального рівняння.
Функція y=y(x,c1..cn), де c1..cn – довільні константи, називають загальним розв’язком рівняння (1), якщо ця функція є розв’язком рівняння (1) при довільному наборі констант.
Функція y=y(x) називається особливим розв’язком рівняння, якщо ця функція є розв’язком рівняння, але із загального розв’язку ії отримати ні при яких константах.
Звичайні диференціальні рівняння 1-го порядку
I. Диференціальні рівняння з відокремленими змінними
f1(x)dx+f2(y)dy=0
Інтегруючи це рівняння:
![]()
II. Диференціал рів-ня з відокремлюваними змінними
m(x)n(y)dx+m1(x)n1(y)dy=0 :(n(y)m1(x))≠0

Значення n(y)=0, m1(x)=0 треба перевірити додатково.
Ці значення x і y, якщо вони є розв’язком рівняння і не
містяться в загальному розв’язку, є особливим
розв’язком рівняння.
III. Диференціальні рівняння, що приводяться до рівнянь з відокремлюваними змінними
1. y’=f(ax+by+c) приводиться до рівняння з
відокремлюваними змінними за допомогою
підстановки ax+by+c=z, де z – нова функція.
Диференціюючи, маємо:
a+by=z’
![]()
Підставивши замість y та y’ іх значення в початкове
рівняння:

2. До диференціальних рівнянь з відокремлюваними
змінними
відносяться рівняння виду:
 IV.
Однорідні диференціальні рівняння.
IV.
Однорідні диференціальні рівняння.
f(x,y) – однорідна, якщо для будь-якого t
f(tx,ty)=tkf(x,y), де k – степінь однорідності. Однорідні диференціальні рівняння приводяться
до рівнянь з відокремлюваними змінними
за допомогою підстановки: y/x=z, y=zx, y’=z’x+z. z’x+z=
f(z). Останнє рівняння є диференціальним з
відокремлюваними змінними. Відокремлюючи змінні,
маємо:

V. Диф. Рівняння, які приводяться до однорідних. 2


Одержимо занальний інтеграл початкового рівня.
VI. Лінійні диф. Рівняння 1-ого порядку
 2).Метод
підстановки
2).Метод
підстановки
Суть метода в слідуючому: розвязок лініного, неоднорідного диф. рівняння

VII. Диф. р-ня Бернуллі 3
![]()
Зауважимо: якщо n=0, то дане р-ня перетворюється в лінійне, а при n=1, то в р-ня з відокремлюваними змінними.
Існує два методи інтегрування диф. р-нь Бернуллі:
1) Метод зведення диф. р-нь Бернуллі до лінійного.
Розділемо все р-ня на уn :
![]()
Диференцюючи
це р-ня маємо:![]()
Підставимо замість у і у’:
![]()
Останнє р-ня є лінійним. Інтегруючи його та повертаючись до старої ф-ції у за доп. заміни у1-n=z – одержемо загальний інтеграл р-ня.
2) Метод підстановки інтегрування диф. р-ня Бернулі
![]()
Підставляючи замість у і у’ їх значення в початкове р-ня:
![]()
Виберемо
ф-цію v
таку,
щоб

Підставляючи замість v його значення в диф. р-ня:

Інтегруючи останнє р-ня знайдемо ф-цію u, а розв’язком буде добуток ф-цій u*v
VIII. Диф. Р-ня в повних диференціалах

Із
теореми про незалежність криволінійного
інтегралу від шляху інтегрування маємо,
що ліва частина диф. р-ня буде повним
диференціалом ф-ції u(x,y)
тоді, коли![]()
Розглянемо один з методів знаходження ф-ції u(x,y)
1)
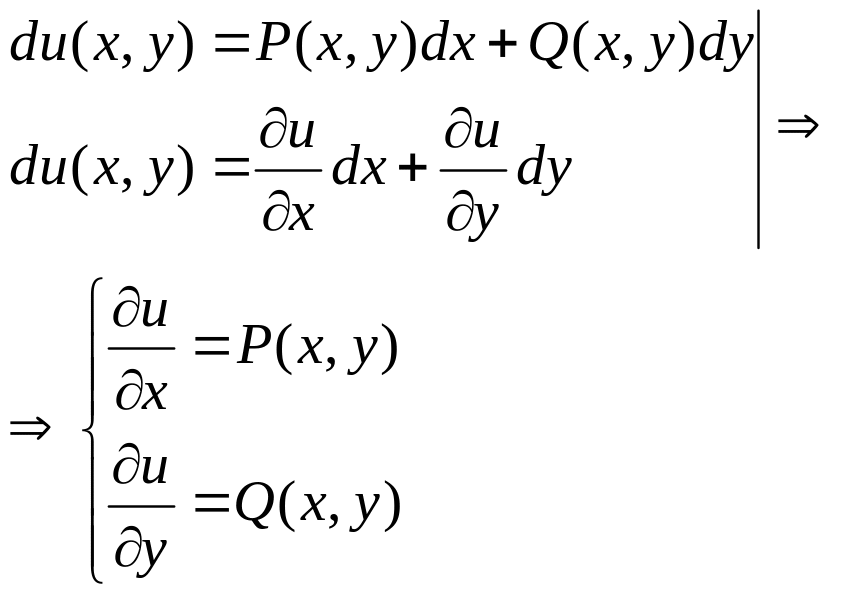
Інтегруючи
довільне з цих р-нь, наприклад перше
маємо:![]()
Щоб знайти ф-цію С(у), то використовуємо ін. умову
![]()
Із останнього р-ня знаходимо С’(у), а потім і саму ф-цію С(у)
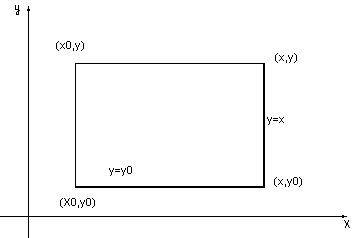
2) P(x,y)dx+Q(x,y)dy=0 – р-ня повних диференціалів, тоді за теоремою про незалежність криволінійного інтегралу від шляху інтегрування будемо мати, що фіксуючи деяку точку (x0,y0) і беручи точку (х,у) будемо інтегрувати по осям
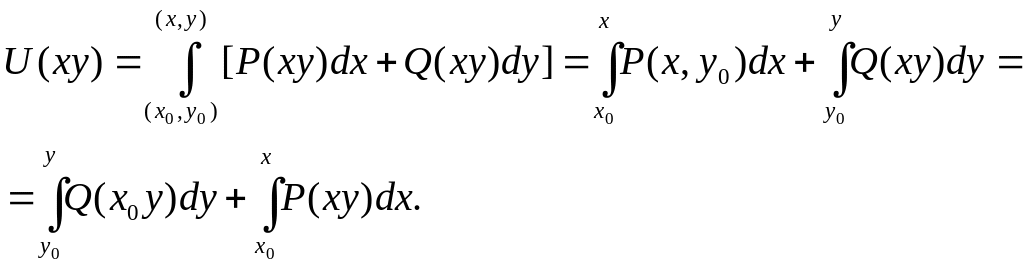
Інтегрувальний множник 4
Припустимо, що P(xy)dx+Q(xy)dy=0 не є рівнянням в повних диференціалах, тобто
 Диференц.
Рівняння які не є диференціальними
рівняннями в повних диференціалах можна
інтегрувати за допомогою метода виділення
повного диференціалу при цьому слід
приміняти формули для обчислення
диференціалу функції
Диференц.
Рівняння які не є диференціальними
рівняннями в повних диференціалах можна
інтегрувати за допомогою метода виділення
повного диференціалу при цьому слід
приміняти формули для обчислення
диференціалу функції
dCx)=Cdx
dxy)=ydx+xdy
d(x/y)=(ydx-xdy)/y2
d(ey)=eydy
d(x2+y2)=2xdy+2ydx.
Диференціальні рів-ня I-го порядку, не розв’язані відносно похідної
I. Диференціальні рівняння І порядку, які можна розв’язати відносно похідної.
Припустимо,
що диференціальне рівняння
![]() ,
можна розв’язати відносно похідної,
тоді одержимо одне або кілька рівнянь
розв’язаних відносно похідної.
,
можна розв’язати відносно похідної,
тоді одержимо одне або кілька рівнянь
розв’язаних відносно похідної.
![]()
![]() одержимо загальний інтеграл цього
рівняння
одержимо загальний інтеграл цього
рівняння
![]()
Загальний
інтеграл цього рівн. записується у
вигляді:
![]()
ІІ.
![]() -
рівн. не містить x
і y,
а тільки похідну. Припустимо, що
-
рівн. не містить x
і y,
а тільки похідну. Припустимо, що
![]() -
є розв’язок рівн.
-
є розв’язок рівн.
![]() ,
тоді
,
тоді
![]()
Підставляючи
замість a,
його значення в загальний розв’язок,
маємо:
![]()
ІІІ.
Рівняння, які не містять невідомої
функції.
![]()
Припустимо, що це рівняння припускає параметризацію.
![]()
![]()
![]()
![]()
![]()
IV.
![]() немає
x
немає
x
Припустимо, що рівн. припускає параметризацію:
![]()
![]()
![]() -
загальний розв’язок цього рівняння.
-
загальний розв’язок цього рівняння.
Диференціальні рівняння Лагранжа 5
Диф.
рівн. Лагранжа наз. рівн.
![]()
![]()
За допомогою введення параметра
Покладемо:
![]()
![]()
![]()
![]() -
останнє
рівняння є лінійним рівнянням.
-
останнє
рівняння є лінійним рівнянням.
Припустимо,
що його загальний розв’язок
![]() -
розв’язок рівняння Лагранжа в
параметричному вигляді.
-
розв’язок рівняння Лагранжа в
параметричному вигляді.
Диференціальне рівняння Клеро
Диф.
рівн. Клеро наз. рівн. виду
![]() ,
це той випадок рівн. Лагранжа, коли
,
це той випадок рівн. Лагранжа, коли
![]()
Рівн. Клеро, як і рівн. Лагранжа будемо розв’язувати за допомогою метода введення параметра.
Покладемо:
![]()
![]()
![]()
![]()
![]()
![]()
![]() -
заг.
розв’язок рівн. Клеро.
-
заг.
розв’язок рівн. Клеро.
![]()
![]()
Лінійні диф. рівняння n-го порядку
![]() x-невідома
змінна;
x-невідома
змінна;
у-невідома функція;
P1(x),P2(x),..,Pn(x)-задані неперервні функції від х;
f(x)- неперервна функція змінної х;
Якщо f(x)=0 хєХ, то рівняння набуває вигляду:
![]()
Лінійним однорідним диф. рів. n-го порядку яке відповідає лінійному неоднорідному диф. рів. (1);
Позначемо ліву частину рівн. (1) і (2) через:
![]() L(y)-
L(y)-
наз. лінійним диференіальним оператором.
Властивості лінійного диф. оператора:
1) Дов.С=const L(Сy)=CL(y)
дійсно
 2)
2)![]()
доведення

Висновок: для дов. Const C1 C2…Cn
![]()
Властивості розв’язків лінійного неоднорідного диф. рів. n-го порядку.
Нехай маємо лінійне диф. рів. n-го порядку (2) та не лінійне (1);
1).
якщо
![]() то для дов. С=const
то для дов. С=const
![]() доведення
доведення
![]() є
роз. рів. (2) то L(y1)=0
розглянемо L(Cy1)=CL(y1)=0
а це і озн. що сума Су1(х)
є розв’язком рівняння (2)
є
роз. рів. (2) то L(y1)=0
розглянемо L(Cy1)=CL(y1)=0
а це і озн. що сума Су1(х)
є розв’язком рівняння (2)
Ч.т.д
2) y1=y1(x) y2=y2(x) розв. (1), то їх сума та різниця у1+у2 теж є рівняння (2); доведення
оскільки у1-є розв’язок (2) то L(y1)=0, L(y2)=0
L(y1+y2)=L(y1)+L(y2)=0 => y1+y2 є розв. (2);
Висновок: якщо y1=y1(x) y2=y2(x) є розв. (2) то якими б не були дов. C=const i=1,n;
![]() теж
буде розв’язки рівн.(2)
теж
буде розв’язки рівн.(2)
3) Якщо комплексна ф-ція U(x)+iV(x) є розв’язком (2) то дійсна частина U(x) і уявна частина V(x) теж є розв. (2);
доведення
U(x)+iV(x) –розв.(2) L(U+iV)=0 Використовуючи вл-сті:
L(U)+iL(V)=0
Відомо що комплексне число =0 тоді і тільки тоді, коли 0 дорівнює і дійсна частина:
![]()
Диф рівняння вищіх порядків 6
І. Диф. рівн. вищіх порядків, які припускають зниження порядку.
Одержимо його загальний
![]()
ІІ. До другого типу диф. рівн., які припускають зниження порядку відносно рівн. виду:
![]()
Це рівн. не містить невідомої ф. y, та похідних цієї ф. до (k-1) порядку включно.
Порядок цього рівн. можна знизити на k одиниць, за допомогою підстановки:
![]() ,
підставляючи в диф. рівн. замість похідних
ф. їх значення, отримаємо
,
підставляючи в диф. рівн. замість похідних
ф. їх значення, отримаємо
![]() ,
припустимо, що останнє рівн. можна
проінтегрувати, припустимо, що
,
припустимо, що останнє рівн. можна
проінтегрувати, припустимо, що![]() -
його загальний розв’язок.
-
його загальний розв’язок.
![]()
Інтегруючи це рівн. k-разів, одержимо загальний розв’язок початкового рівн.
ІІІ Диф. рівняння які не містять незалежної змінної:
![]()
порядок цього рівняння можна знизити за допомогою підстановки z=y’, де z=z(y)=>y(x), то z- складена функція від x. z=z(x);

Аналогічно знаходяться похідні вищих порядків. Підставляючи в диф. рівн. замість похідних від функції їх значення одержимо диф. рівняння (n-1) порядку. Припустимо що одержане диф рівняння можна проінтегрувати і нехай
![]()
повертаючись
до старої функції у
![]()
Останнє
рівняння є диф рівн. з відокремлювальними
змінними
![]()
Інтегруючи останнє рівняння одержимо загальний інтеграл початкового рівн.
ІV. Однорідні диф. рів. вищих порядків:
![]() -
наз. однорідною відносно невідомої
ф-ції y
та її похідних якщо дов. t
(const, або змінна).
-
наз. однорідною відносно невідомої
ф-ції y
та її похідних якщо дов. t
(const, або змінна).
![]()
Число к- степінь однорідності однорідні диф. рів. вищих порядків інтегруються за допомогою підстановки:
![]() -
де z
нова невідома функція
-
де z
нова невідома функція
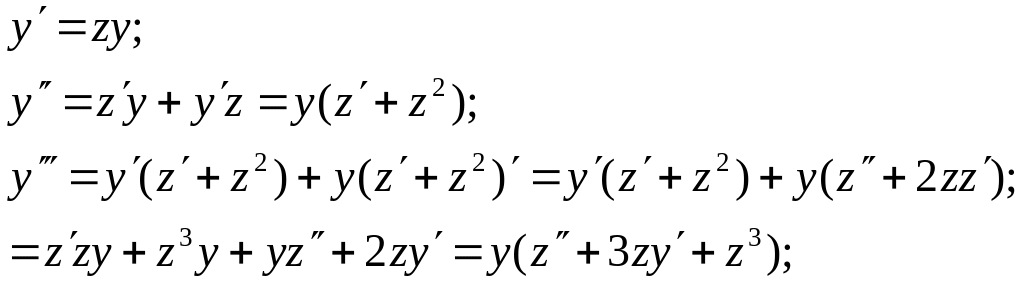 Аналогічно
обчислюються похідні вищих порядків
Підставляючи в диф. рівн. замість похідних
від функції z
їх значення одержимо диф. рівняння
(n-1) порядку. Припустимо що одержане диф
рівняння можна проінтегрувати і нехай
Аналогічно
обчислюються похідні вищих порядків
Підставляючи в диф. рівн. замість похідних
від функції z
їх значення одержимо диф. рівняння
(n-1) порядку. Припустимо що одержане диф
рівняння можна проінтегрувати і нехай
![]() Повертаючись до старої невідомої функції
у
Повертаючись до старої невідомої функції
у
![]()
Інтегруючи останнє рівняння:
![]()
![]()
V. Диф. рів. ліва частина яких є точною похідною деякої функції:
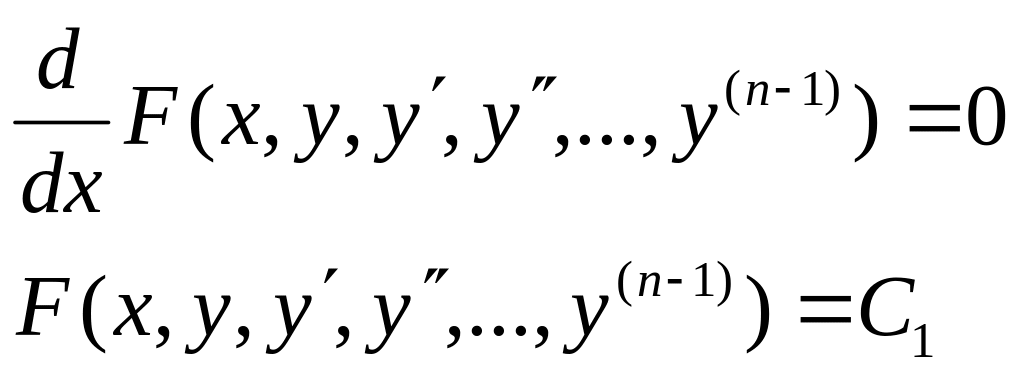
останнє рівняння є диф. рів. (n-1)- порядку інтегруючи це рівняння одержимо загальний його інтеграл.
Лінійно залежні та лінійно незалежні розв’язки 7 лінійного однорідного диф. рів-ня
![]()
розв.(2) y1=y1(x)…y2=y2(x) наз. лінійнозалежними на відрізку [a,b], якщо існують const.
![]() із яких хоч би одна
відмінна від 0, такі що виконувалась
рівність:
із яких хоч би одна
відмінна від 0, такі що виконувалась
рівність:
![]() Припустимо n
не
равно 0
Припустимо n
не
равно 0
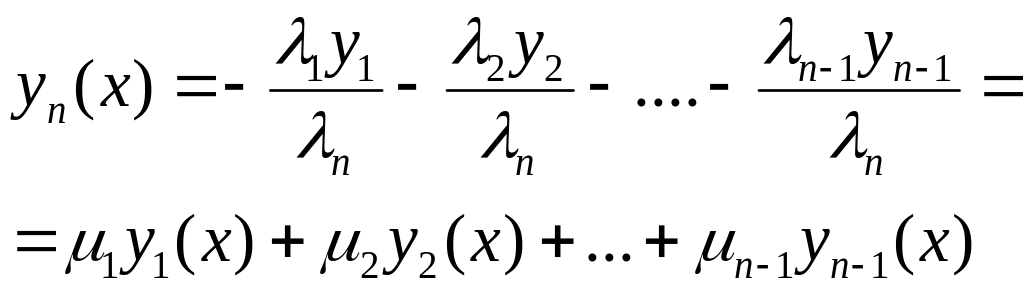
Вираз, який стоїть в правій частині останньої рівності наз. лінійною комбінацією ф-цій у1(x), у2(x) і т.д. уn-1(x);
Функції у1(x), у2(x) і т.д. уn-1(x) наз. лінійною залежна на відрізку [a,b] якщо хоч би одна із ф-цій є лінійно залежною.
Функції у1(x), у2(x) і т.д. уn-1(x); наз. лінійною незалежна на відрізку [a,b] якщо
![]()
якщо рівність виконується тільки 1=2=…=n=0
1) 1,x,x2,…,xn –лінійно залежні на відр.[a,b]
на дов. [a,b] числової прямої. Розглянемо дов. комбінацію цих функцій
![]()
Останнє рівняння є рів. n-го степеня. а тому воно може мати не більше ніж n коренів, а значить перетворюється в 0 не більше ніж в n точках, а значить в кожній точці відрізка [a,b] ця рівність виконуватися не може. Покажемо що
2).![]() є
лінійно незалежною
є
лінійно незалежною
к1 <>к1<>…<>kn. на дов. [a,b], дов. будемо доводити від супротивного.
Доведення
Припустимо є лінійно залежною
к1
<>к1<>…<>kn. на дов.
[a,b], тоді за озн. лінійної залежності
ф-цій маємо що існують const
![]()
із яких
хоч би одна не дорів. 0 такі що
![]()
Розділемо
останнє рівняння на
![]() одерж.
одерж.
![]()
Продиференціюємо останню рівність по х:
![]()
Поділемо
на
![]() :
:
![]()
Продиф останю нерівність:
Продовжуючи цей процес одержимо після n-го кроку слідуючу тотожність
![]()
Одержана суперечність і доводить цю властивість
3). Якщо у1,у2,…уn, лінійно залежні розв’язки рівн. (2) то визначник Вронського цієї системи
W(x)=0 для дов. xє[a,b].
Оскільки ф-цій у1,у2,…уn, є лінійно залежними розв’язками рівн. (2), то за озн. лінійної залежності сист. функцій, маємо хоч би одне із цих функцій є лінійною комбінацією інших.
Припустимо:![]()
Підставляючи замість yn та похідних цієї функції їх значення в визначник вронського маємо:
![]()
Одержаний визначник =0 тому що останній стовбець визн. є лінійною залежністю інших стовбців.
4). Теорма про загальний розв’язок лінійного однорідного диф. рівняння n-го порядку:
у1,у2,…уn- лінійно незалежні розв. рівняння.(2)
то загальний розв’язок рівн.(2) має вигляд
![]()
де С1,С2,…,Сn,- дов. константи є загальними розв’язками (2);
Доведення
yi=yi(x)
i=1,n розв.(2) =>
![]()
Підставляємо замість
![]()
в диф. рівняння (2)
![]()
Останнє рівняння озн. що функція y є розв’язком лінійного одн. рівняння (2) Оскільки це функція містить n-дов const то вона є загальним розв’язком цього рівняння.
Визначник Вронського
Нехай маємо лінійне однорідне диф. рів. (2) і нехай у1,у2,…,уn – розв’язки цього рівняння
Розглянемо визначник:
![]()
цей визначник наз визначником Вронського
Лінійні однорідні диф. рівняння зі сталими 8 коефіцієнтами
![]()
аі=Const для дов і=1,n
Розв’язок ріняння (2) будемо шукати у=ekx (3)
![]()
Підставляючи в (2) замість у і похідні від у їх значення одержимо слідуючу тотожність
![]()
![]()
![]() (4)
(4)
характеристичне рівняння (2)
Характерестичним рів. записуетья зразу по виду диф. рівн., замінюючи тільки похідні від функції у відповідні степені к.
Оскільки х-тичне рівн.(4) є алгебраїчним рівн. n-го степеня то воно має n-коренів
Можливі випадки:
![]()
ці функції є лінійно незалежними на відрізку [a,b], а тому загальним розв’зком рів.(2)
![]()
2).Серед коренів хар-ного рівня є корені комплексні:
k1=a+ib k2=a-ib y1=e(a+ib)x=eax(cosbx+isinbx)
За 3 властив. розв’язків лінійного диф рів-ня маємо,що:
y11=eaxcosbx y12=eaxsinbx
Ці розв’язки лінійно незалежні.
k2=a-ib y2’= eaxcosbx
y2’’= -eaxsinbx – лінійно залежні з y11 та y12
y=eax(C1cosbx+C2sinbx)
3).Серед коренів хар-ного рів-ня є корені кратні:
k1= k2=……..= kn
Часткові розв’язки диф. рів-ня 2:
y1=ek1x y2=xek1x y3=x2ek1x ym=xm-1ek1x
y=ek1x(C1+C2x+…Cmxm-1)
Якщо кратними є комплексні корені:
k1= k2=a+ib k3= k4=a-ib
y=eax((C1+C2x)cosbx+(C3+C4x)sinbx)
Лінійні неоднорідні диференціальні рівняння n-го порядку
Має вигляд: y(n)+P1(x)y(n-1)+..+Pn(x)y=f(x) (1)
y(n)+P1(x)y(n-1)+..+Pn(x)y=0 (2)
L(y)=f(x) (1’)
L(y)=0 (2’)
Теорема 1: y=y1(x) - розв’язок (2) =>
y=y2(x) – розв’язок (1)
=> y1(x)+-y2(x)
Оскільки
y=y1(x) - розв’язок (2) => L(y1)=0
y=y2(x) – розв’язок (1) => L(y2)=f(x)
L(y1+-y2)=L(y1)+-L(y2)=f(x) => y1+-y2
Теорема 2 (теорема про загальний розв’язок лінійного
неоднорідного диференціального рівняння n-го
порядку): Якщо y0 – загальний розв’язок (2),
yч - частинний розв’язок (1), тоді y=y0+yч.
Доведення: Оскільки y0 – загальний розв’язок (2), то
він є лінійною комбінацією n часткових розв’язків
(2). Оскільки yч – частинний розв’язок рівняння (1),
то за вищедоведеною теоремою y=y0+yч
Лінійні неоднорідні диференціальні рівняння зі сталими коефіцієнтами
y(n)+a1y(n-1)+..+any=f(x) (1)
y(n)+a1y(n-1)+..+any=0 (2)
Частинний розв’язок рівняння (1) можна знайти у двох випадках:
1) f(x)=Pm(x)eax, де Pm – многочлен m-го степеня, a - деяка
константа.
ym=Qm(x)eaxxk, де Qm(x) – многочлен степеня m з
невідомими коефіціентами. k - число коренів
характеристичного рівняння, рівних a.
Щоб знайти невідомі коефіцієнти многочлена Qm(x),
треба в рівняння (1) підставити значення функціі y та
ії похідних. Одержану після цього тотжність скороти-
ти на eax і після цього прирівняти коефіцієнти при од-
накових степенях x в лівій і правій частинах. Із одер-
жаної системи знаходимо невідомі коефіцієнти.
2) f(x)=eax(P1(x)cosbx+P2(x)sinbx)
a і b – деякі константи. P1(x) і P2(x) – задані
многочлени, причому один з них може дорівнювати 0.
y2=eax(Q1(x)cosbx+Q2(x)sinbx)xk, де Q1(x) і Q2(x) - мно-
гочлени одного степеня з невизначеними коефіцієн-
тами. Степінь цих многочленів дорівнює вищому із
степеней многочленів P1(x) та P2(x). Число k дорівнює
числу коренів характеристичного рівняння, рівний чис-
лу a+ib. Невизначені коефіцієнти многочленів Q1(x) і
Q2(x) знаходяться за допомогою метода невизначених
коефіцієнтів. Суть його у слідуючому:
в початкове дифренціальне рівняння замість y
підставляємо yч, одержимо тотожність, скоротимо на
eax. Після цього прирівнюємо коефіцієнти при cosbx та
sinbx в обох частинах. Потім в одержаній тотожності
прирівнюємокоефіцієнти при однакових степенях x. В
результаті одержимо систему лінійних рівнянь, із якої
і знаходимо всі невизначені коефіцієнти.
Метод варіації довільних сталих при інтегруванні 9 лінійного однорідного диф. рів-ня n-го порядку
Нехай
маємо :![]()
![]()
Припускаємо,
що заг розв’язок (2):![]()
Заг
розв’язок р-ня (1) будемо шукати у точно
такому вигляді як розв р-ня (2). Тільки
замість констант виб ф-ї:
![]()
Знайдемо
похідну від у
![]()
Виберемо
ф-ї такими щоб сума
![]()
Знайдемо
похідну другого порядку від у
![]()
Знову
виберемо ф-ї СК
(х)
такими щоб
![]() таким чином отримаємо:
таким чином отримаємо:
![]()
Підставимо у (1) значення у та його похідних їх значення


Оскільки
основний визначник цієї системи є
визначником Вронського, лінійно незал
розв’язків
ЛОДР n-го
порядку, а тому цей визначник відмінний
від 0 і тому ця система має єдиний
розв’язок нехай![]() - розв’язки даної сист.
- розв’язки даної сист.
![]()
Підставляючи маємо:
![]()
Диференціальні рів-ня Ейлера
р-ня
виду:
![]()
ДРЕ приводиться до ЛДР n-го порядку зі сталими коеф за доп підстановки х=еt у=у(х)=у(t).
Викор ф-лу для обчисл похідної від ф-ї заданої парам р-ми маємо:
![]()
![]()
Продовжуючи знаходити похідні та підставляючи їх одержимо ЛДР зі сталими коеф.
Інтегруючи та повертаючись до старої змінної Х одержимо заг розв ДРЕ.
Зауважимо,
що для ДР виду
![]() Викор
підстановка ах+b=еt.
Викор
підстановка ах+b=еt.
Системи звичайних диференціальних рівнянь 10
система
виду:

Х – незал змінні. У – невідомі ф-ї. F – задані ф-ї своїх аргументів.
Якщо
цю систему можна розв’язати відносно
похідних то система набуває виду:

(1)- нормальна система звич ДР. У1=У1(Х), .... , Уn=Уn(Х) – розв’язки системи (1)
 -
заг розв’язок сист (1) при умовах:
-
заг розв’язок сист (1) при умовах:
– при дов наборі С1,...,Сn ф-ї У1, .... , Уn – розв (2)
– к ожне
із рівнянь наз 1-м інтегралом даної
системи
ожне
із рівнянь наз 1-м інтегралом даної
системи
Розв сист це значить знайти n незал перших її інтегралів.
Системи диф. рівнянь в симетричній формі
Називають
![]() у
вигляді нормальної
у
вигляді нормальної
![]()
Вірне також і обернен твердження, якщо система записана у вигляді нормальної, її можна записати у вигляді системи в симетричній формі
Основні методи інтегрування звичайних диф. рівнянь
I. Метод зведення системи до 1 рв
Суть методу: одне із рівняь диференціюємо (n-1) раз після кожного разу підставляємо в систему значення похідних. Із першого рівняння та одержаних (n-1) рівнянь вилучемо всі невідомі функції через у1 і підставимо ці значення в одержане вище рівняння. Інтегруючи, знайдемо невідому у1. Всі інші невідомі функції знаходяться операцією диференціювання.
II. Метод інтегровних комбінацій
Інтегровні комбінації – це легкоінтегровне диференціальне рівняння.
Щоб одержати загальний розв’язок бажано систему записати в симетричній формі і знайти для неї (n-1) незалежних перших інтегралів. Для знаходження використовують метод інтегрованих комбінацій. Для побудови інтегровних комбінацій широко використовують слідуючи властивість:
![]()
має місце
![]()
насправді:
![]()
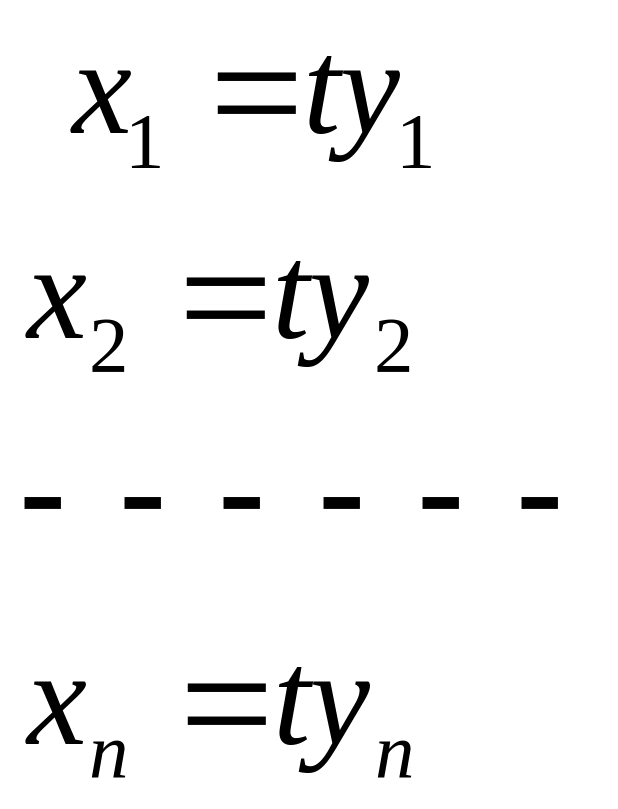
![]()
1).Диференціальні рівняння
Звичайні диференціальні рівняння 1-го порядку
Диференціальні рівняння з відокремленими змінними
Диференціал рів-ня з відокремлюваними змінними
Диференціальні рівняння, що приводяться до рівнянь з відокремлюваними змінними
Однорідні диференціальні рівняння
2).Диф. рівняння, які приводяться до однорідних
Лінійні диф. рівняння 1-ого порядку:
Метод варіації довільної сталої
Метод підстановки
3).Диф. р-ня Бернуллі
Диф. р-ня в повних диференціалах
4).Інтегрувальний множник
Диференціальні рів-ня I-го порядку, не розв’язані відносно похідної
5).Диференціальні рівняння Лагранжа
Диференціальне рівняння Клеро
Лінійні диф. рівняння n-го порядку
Властивості лінійного диф. оператора
Властивості розв’язків лінійного неоднорідного диф. рівняння n-го порядку
6).Диф рівняння вищіх порядків:
які припускають зниження порядку
які не містять незалежної змінної
однорідні
ліва частина яких є точною похідною деякої функції
7)Лінійно залежні та лінійно незалежні розв’язки лінійного однорідного диф. рів-ня
Теорма про загальний розв’язок лінійного однорідного диф. рівняння n-го порядку
Визначник Вронського
8)Лінійні однорідні диф. рівняння зі сталими коефіцієнтами
Лінійні неоднорідні диференціальні рівняння n-го порядку
Лінійні неоднорідні диференціальні рівняння зі сталими коефіцієнтами
9).Метод варіації довільних сталих при інтегруванні лінійного однорідного диф. рів-ня n-го порядку
Диференціальні рів-ня Ейлера
10).Системи звичайних диференціальних рівнянь
Системи диф. рівнянь в симетричній формі
Основні методи інтегрування звичайних диф. рівнянь
