
- •2) Теорема Тейлора для функций от одной вещественной переменной:
- •2.1) Формулировка теоремы
- •2.2 Формулы для остатка:
- •2.3 Оценки остатка
- •2.4 Доказательство теоремы:
- •2.5 Пример:
- •3)Теорема Тейлора для функций от нескольких переменных:
- •3.1Частные производные. Мультииндекс. Обозначения
- •3.2 Обобщение формулы Бинома Ньютона
- •3.3Теорема 1 (Формула Тейлора с остаточным членом в форме Лагранжа)
- •3.4 Теорема 2 (Формула Тейлора с остаточным членом в форме Пеано)
3)Теорема Тейлора для функций от нескольких переменных:
3.1Частные производные. Мультииндекс. Обозначения
Пусть ![]() m
раз дифференцируемая функция, т.е.
имеет все частные производные порядка
1,2, …, m , непрерывные в области D.
m
раз дифференцируемая функция, т.е.
имеет все частные производные порядка
1,2, …, m , непрерывные в области D.
Тогда
по теореме о равенстве смешанных
производных производную k-ого
порядка ![]() можно записать в виде
можно записать в виде
![]()
где ![]() число
дифференцирований по переменной
число
дифференцирований по переменной ![]()
![]() число
дифференцирований по переменной
число
дифференцирований по переменной ![]() …
,
…
,
![]() число
дифференцирований по переменной
число
дифференцирований по переменной ![]() Очевидно
Очевидно ![]()
Пусть ![]() .
Положим
.
Положим ![]() .
Для
.
Для ![]() введем обозначения
введем обозначения ![]() .
Тогда производную можно кратко
записать в виде
.
Тогда производную можно кратко
записать в виде
![]()
Для
мультииндекса
положим также ![]()
3.2 Обобщение формулы Бинома Ньютона

где
сумма берется по всем целым
неотрицательным решениям уравнения
![]()
3.3Теорема 1 (Формула Тейлора с остаточным членом в форме Лагранжа)
Пусть
m+1
раз дифференцируемая функция в
области D,
точки ![]() причем
отрезок прямой
причем
отрезок прямой ![]() соединяющий точки
соединяющий точки ![]() целиком
лежит в D.
Тогда справедлива формула
целиком
лежит в D.
Тогда справедлива формула

где ![]() некоторое число. Поскольку под
знаком суммы
некоторое число. Поскольку под
знаком суммы ![]() ,
то имеем
,
то имеем

Отметим,
что для n=1
данная формула целиком совпадает с
формулой Тейлора с остаточным членом
в форме Лагранжа.
Доказательство.
Рассмотрим функцию одной переменной ![]()
Данная
функция m+1
раз дифференцируема по параметру
![]() ,
причем
,
причем
![]() Используя
формулу Тейлора для функции одной
переменной, получаем
Используя
формулу Тейлора для функции одной
переменной, получаем
![]() где
где ![]()
Имеем
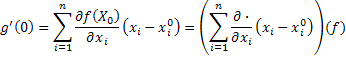

Но

Используя мультииндексы, получаем

Аналогично получаем
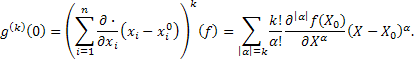
Отметим также, что

3.4 Теорема 2 (Формула Тейлора с остаточным членом в форме Пеано)
Пусть
m
раз дифференцируемая функция в
некоторой окрестности точки ![]() .
Тогда
.
Тогда ![]() допускает
представление
допускает
представление
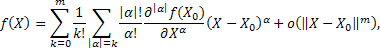
где
через ![]() обозначена
функция вида
обозначена
функция вида
![]()
при
этом известно, что ![]() –
некоторая непрерывная функция в
точке
–
некоторая непрерывная функция в
точке ![]()
Доказательство.
Поскольку ![]() m
раз дифференцируемая функция в
некоторой окрестности точки
m
раз дифференцируемая функция в
некоторой окрестности точки ![]() ,
то найдется такое число
,
то найдется такое число ![]() что в шаре
что в шаре ![]() функция
имеет
непрерывные частные
функция
имеет
непрерывные частные
производные вплоть до порядка m включительно.
Пусть
![]() единичная
сфера,
единичная
сфера, ![]() .
.
При ![]() поэтому функция одной переменной
поэтому функция одной переменной ![]() имеет
в интервале
имеет
в интервале ![]() непрерывные
производные до порядка m
включительно
непрерывные
производные до порядка m
включительно![]() Используя
формулу Тейлора с остаточным членом в
форме Лагранжа, получаем
Используя
формулу Тейлора с остаточным членом в
форме Лагранжа, получаем
![]()
где Теперь для доказательства теоремы достаточно установить справедливость следующей леммы.
Лемма. ![]() ,
и при этом функция
,
и при этом функция
![]() непрерывна
в точке
непрерывна
в точке ![]()
Доказательство. Имеем
![]()
Поэтому
 Следовательно
Следовательно
Теперь,
очевидно, что утверждение леммы
вытекает из непрерывности всех
частных производных m-ого
порядка в шаре ![]() Заметим теперь, что
Заметим теперь, что ![]()
![]() Лемма
и теорема доказаны.
Лемма
и теорема доказаны.
