
Основные свойства бесконечно малых последовательностей
▼ Теорема 2.2. Сумма и разность двух бесконечно малых последовательностей являются бесконечно малыми последовательностями.
Доказательство.
Пусть
и
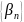 — бесконечно малые последовательности.
Докажем, что последовательность
— бесконечно малые последовательности.
Докажем, что последовательность
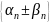 бесконечно малая.
Пусть
- произвольное положительное число,
бесконечно малая.
Пусть
- произвольное положительное число,
 - номер, начиная
с которого
- номер, начиная
с которого
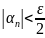 ,
а
— номер,
начиная с которого
,
а
— номер,
начиная с которого
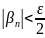
(такие
номера найдутся согласно определению
бесконечно малой последовательности
6). Возьмем
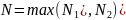 .
Тогда при
одновременно
выполняются два неравенства:
и
.
Значит, при
всех
.
.
Тогда при
одновременно
выполняются два неравенства:
и
.
Значит, при
всех
.
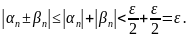
Но
тогда, согласно определению 6,
последовательность
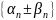 бесконечно
малая, что и требовалось доказать. ▲
бесконечно
малая, что и требовалось доказать. ▲
С л е д с т в и е. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
▼ Теорема 2.3. Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Доказательство.
Пусть
и
—
бесконечно малые последовательности.
Докажем, что последовательность
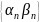 бесконечно малая.
Возьмем для первой последовательности
произвольное положительное
число
,
а для последовательности
в
качестве
возьмем 1. Согласно
определению бесконечно малой
последовательности: для
найдется
такой номер
,
что
при
;
а для
найдется
такой
номер
бесконечно малая.
Возьмем для первой последовательности
произвольное положительное
число
,
а для последовательности
в
качестве
возьмем 1. Согласно
определению бесконечно малой
последовательности: для
найдется
такой номер
,
что
при
;
а для
найдется
такой
номер
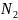 ,
что
,
что
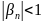 при
.
при
.
Примем , тогда при будут выполнены оба неравенства.
Значит, при

Это и означает, что последовательность бесконечно малая. ▲
Следствие. Произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
▼ Теорема 2.4. Произведение бесконечно малой последовательности на ограниченную последовательность является бесконечно малой последовательностью.
Доказательство.
Пусть
—
ограниченная, а
-
бесконечно малая
последовательности. Докажем, что
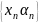 бесконечно
малая последовательность. В силу
ограниченности последовательности
существует
такое число А,
что
любой элемент ее удовлетворяет
неравенству
бесконечно
малая последовательность. В силу
ограниченности последовательности
существует
такое число А,
что
любой элемент ее удовлетворяет
неравенству
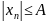 .
Поскольку
последовательность
бесконечно
малая, для
положительного
числа
.
Поскольку
последовательность
бесконечно
малая, для
положительного
числа
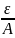 существует
такой номер N,
что при всех
выполняется
неравенство
существует
такой номер N,
что при всех
выполняется
неравенство
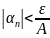 . Значит, при
. Значит, при
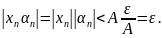
Это
и означает, что последовательность
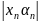 бесконечно
малая. ▲
бесконечно
малая. ▲
Следствие. Произведение бесконечно малой последовательности на постоянное число является бесконечно малой последовательностью.
