
1.5. Абсолютная величина числа
По определению абсолютная величина вещественного числа х (модуль числа)
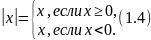
Рассмотрим свойства абсолютной величины.
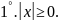
Это свойство непосредственно вытекает из определения модуля числа: если число неотрицательно, его абсолютная величина равна самому числу; модуль отрицательного числа равен этому числу, взятому с обратным знаком.
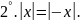
Также следует из определения модуля числа (1.4).

Если
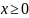 ,
то
,
то
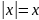 и
тогда
и
тогда
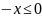 ,
отсюда
,
отсюда
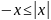 ,
т.е.
,
т.е.
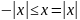 ;
;
если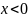 ,
то по выражению (1.4)
,
то по выражению (1.4)
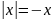 ,
откуда
,
откуда
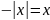 .
Но так как
.
Но так как
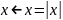 ,
то и получаем
,
то и получаем
 .
.
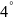 .
Пусть а — положительное число, тогда
неравенства
.
Пусть а — положительное число, тогда
неравенства
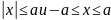 равносильны.
равносильны.
Пусть
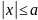 ,
выведем
отсюда второе неравенство.
,
выведем
отсюда второе неравенство.
Если
,
то
,
т.е.
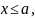 или
или
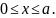
Если
, то
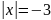 ,
откуда
,
откуда
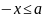 ,
или
,
или
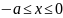 .
.
Объединяя полученные неравенства, получаем
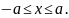
Пусть
теперь справедливо неравенство
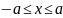 ;
покажем,
что отсюда
следует первое неравенство. Действительно,
одновременно выполняются
неравенства
;
покажем,
что отсюда
следует первое неравенство. Действительно,
одновременно выполняются
неравенства
 и
и
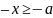 .
Из
второго неравенства имеем:
.
По определению
модуля числа [см. формулу (1.4)] он равен
либо
.
Из
второго неравенства имеем:
.
По определению
модуля числа [см. формулу (1.4)] он равен
либо
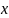 ,
либо
,
либо
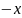 ,
т.е. отсюда и следует, что
.
,
т.е. отсюда и следует, что
.
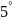 .
Для
любых двух действительных чисел
и
.
Для
любых двух действительных чисел
и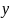 справедливо неравенство
справедливо неравенство
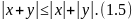
По
свойству
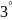
 ,
,

Складывая эти неравенства почленно, получаем
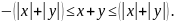
Но по свойству эти неравенства равносильны двойному неравенству (1.5).
В это свойство можно включить также и двойное неравенство
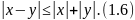
 .
Для
любых двух действительных чисел х и у
справедливо неравенство
.
Для
любых двух действительных чисел х и у
справедливо неравенство
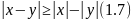
Очевидно тождество для любых двух чисел х и у
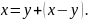
По свойству

откуда и получаем утверждение (1.7).
Глава 2. Предел последовательности
2.1. Числовые последовательности
Числовые последовательности и операции над ними
Числовые
последовательности представляют собой
бесконечные множества чисел. Примерами
последовательностей могут служить:
последовательность
всех членов арифметической и геометрической
прогрессий,
последовательность приближенных
значений
 последовательность периметров правильных
n-угольников,
вписанных в данную окружность. Уточним
понятие числовой последовательности.
последовательность периметров правильных
n-угольников,
вписанных в данную окружность. Уточним
понятие числовой последовательности.
■ Определение
1. Если
каждому числу п
из
натурального ряда чисел
1, 2, 3, .:., п,
... поставлено
в соответствие вещественное число
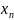 ,
то
множество
вещественных чисел
,
то
множество
вещественных чисел
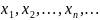
называется числовой последовательностью или просто последовательностью.
Числа
будем
называть элементами,
или
членами,
последовательности
(2.1), символ
— общим элементом, или
членом, последовательности,
а число п
—
его номером.
Сокращенно
последовательность (2.1) будем обозначать
символом
 .
Например, символ
.
Например, символ
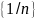 обозначает
последовательность чисел
обозначает
последовательность чисел
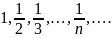
Иными
словами, под последовательностью можно
понимать бесконечное
множество занумерованных элементов
или множество пар чисел
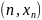 ,
в
которых первое число последовательно
принимает значения
1, 2, 3,... . Последовательность считается
заданной, если указан способ
получения любого ее элемента. Например,
формула
,
в
которых первое число последовательно
принимает значения
1, 2, 3,... . Последовательность считается
заданной, если указан способ
получения любого ее элемента. Например,
формула
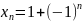 определяет
последовательность 0, 2, 0,
2, ... .
определяет
последовательность 0, 2, 0,
2, ... .
Геометрически
последовательность изображается на
числовой оси в
виде последовательности точек, координаты
которых равны соответствующим
членам последовательности. На рис. 2.1
изображена последовательность
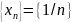 на
числовой прямой.
на
числовой прямой.

Рис.2.1
Рассмотрим
арифметические действия над числовыми
последовательностями. Пусть даны
последовательности
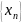 и
и
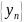 .
.
Суммой последовательностей назовем последовательность
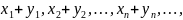 или
или
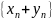 ,
разностью —
,
разностью —
последовательность
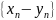 или
или
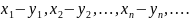
Произведением последовательности на число т назовем последовательность
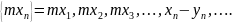
Произведением последовательностей назовем последовательность

Частным назовем последовательность
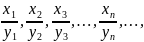
если все члены последовательности отличны от нуля.
