Хуета / Примеры вычисленич производных
.docx
Таблица производных
,
R, (7.1)
в частности, 
,
,
(7.2)
,
. (7.3)
,
R,
, (7.4)
в частности,
.
(7.5)
,
, (7.6)
в частности,
.
(7.7)
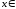R. (7.8)
,
R. (7.9)
Z. (7.10)
,
Z. (7.11)
(–1,
1). (7.12)
,
(–1,1). (7.13)
R. (7.14)
,
R. (7.15)
R, (7.16)
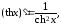
R,
R,
кроме х
= 0. (7.17)
Правила дифференцирования
Пусть
и
–
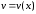дифференцируемые функции х.
,
где С –
const. (7.18)
,
где С –
const. (7.19)
.
(7.20)
. (7.21)
(7.22)
Если y=y(u), а u=u(x), то
(7.23)
Пример
7.4. Вычислить
,
если
►
=
+
(использованы формулы (7.20), (7.21) для
производной суммы и произведения двух
функций, формулы (7.1),
(7.13), (7.19) и (7.23) – правило дифференцирования
сложной функции. Окончательно для
получаем:
.◄
Пример 8.1.
Найти
,
если
.
►Считая, что равенство из условия задачи задаёт у как неявную функцию х,
продифференцируем
обе его части по х,
рассматривая arctgy
как сложную функцию х:
.
Перенесём в левую часть все члены,
содержащие
,
и вынесем из них
за скобки:
.
Отсюда
.◄
Пример 8.2.
Найти
,
если
.
►Из условия
примера имеем:
.
Считая у
неявной
функцией х,
возьмём производные по х
от обеих частей последнего равенства:
или
(дробь
заменена на
).
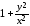После упрощений получаем
,
отсюда
.◄
2º. Понятие функции, заданной параметрически. Вычисление производных от таких функций. Зависимость переменной у от переменной х может быть задана через посредство третьей переменной, которую, как правило, обозначают через t и называют параметром.
Определение 8.2. Пусть х и у заданы как функции t:
. (8.5)
Если функция
на
промежутке
имеет обратную
,
то на множестве
определена
сложная функция от х:
,
называемая функцией, заданной параметрически равенствами (8.5).
Формула для производной функции, заданной параметрически, следует из правил дифференцирования сложной и обратной функции (§6). Имеем
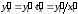. (8.6)
Замечание
8.1. Формулу
(8.6) можно также получить, рассматривая
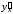как отношение дифференциалов dy
и dx
(замечание (3.2)):
=
.
Вычислив dy
и dx:
dy
dx
,
подставив эти равенства в выражении
для
и произведя сокращения, приходим к
формуле
(8.6).
Пример 8.4.
Найти
,
если
.
►
.
Подставив выражения для
и
в формулу (8.6), имеем:
◄