
Хуета / Анализ бесконечно малых
.docx§ 1. Сравнение бесконечно малых функций
Определение
1.1. Пусть
функции α(x)
и β(x)
являются
бесконечно малыми при х а.
а.
-
Если существует
 ,
то α(x)
и β(x)
называются бесконечно малыми одного
порядка при х
,
то α(x)
и β(x)
называются бесконечно малыми одного
порядка при х а.
а.
-
Если существует
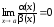 ,
то α(x)
называется величиной более высокого
порядка малости, чем β(x)
при х
,
то α(x)
называется величиной более высокого
порядка малости, чем β(x)
при х а.
а.
Обозначение:
α(x) = o(β(x))
при х а
(α(x)
есть о малое
от β(x)).
а
(α(x)
есть о малое
от β(x)).
-
Если не существует
 ,
то бесконечно малые α(x)
и β(x)
называются несравнимыми при х
,
то бесконечно малые α(x)
и β(x)
называются несравнимыми при х а.
а.
Например,
sin 2x
и
2x
и
 – бесконечно малые одного порядка при
х
– бесконечно малые одного порядка при
х 0,
так как
0,
так как
 .
Функция sin
.
Функция sin 2x
имеет более
высокий порядок малости, чем х
при х
2x
имеет более
высокий порядок малости, чем х
при х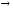 0
(или sin
0
(или sin 2x=о(х)
при х
2x=о(х)
при х 0),
поскольку
0),
поскольку

 Бесконечно малые
Бесконечно малые
 и α(x)
и β(x) = х
несравнимы при х
и α(x)
и β(x) = х
несравнимы при х 0,
так как
0,
так как

 а
а
 не существует (это можно показать с
помощью определения предела функции
на языке последовательностей).
не существует (это можно показать с
помощью определения предела функции
на языке последовательностей).
Замечание
1.1. Если
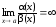 ,
то
,
то
 Тогда β(x) = o(α(x))
при х
Тогда β(x) = o(α(x))
при х а.
а.
Сравнить
две бесконечно малые функции – это
значит установить, что они являются
бесконечно малыми одного порядка, или
что одна из них более высокого порядка,
чем другая, или что они несравнимы. Для
этого надо найти предел их отношения,
т.е. раскрыть неопределённость
 .
.
Определение
1.2. Если
существует
 ,
то α(x)
и β(x)
называются эквивалентными бесконечно
малыми при х
,
то α(x)
и β(x)
называются эквивалентными бесконечно
малыми при х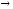 а.
а.
При
отыскании предела отношения бесконечно
малых α(x)
и β(x)
при

используется теорема о замене эквивалентными в отношении и таблица эквивалентных бесконечно малых функций, так как для α(x) и β(x) полезно найти эквивалентные бесконечно малые простейшего вида С(х – а)k.
Таблица эквивалентных бесконечно малых функций.
Пусть
функция
 при
при
 .
Тогда
.
Тогда
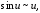

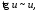
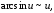



 .
.
Пример
1.1. Сравнить
бесконечно малые α(x) = и β(x) =
и β(x) = при
при
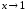 .
.
►α(x) = ~
~
 Þα(x)~
Þα(x)~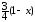 (здесь использована формула
(здесь использована формула
 ,
где
,
где
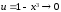 при
при
 ,
,
 ).
Имеем: β(x)=
).
Имеем: β(x)= ~
~ =
=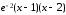 Þ
Þ ~
~ ,
здесь использована формула
,
здесь использована формула
 где
где
 при
при
 .
В результате применения теоремы о замене
эквивалентными в отношении получим:
.
В результате применения теоремы о замене
эквивалентными в отношении получим:
 ¹0,
∞. Поэтому заключаем, что α(x)
и β(x)
бесконечно малые одного порядка при
¹0,
∞. Поэтому заключаем, что α(x)
и β(x)
бесконечно малые одного порядка при
 .◄
.◄
Пример
1.2. Сравнить
бесконечно малые
 и
и
 при
при
 .
.
►Имеем
 ~
~ ~
~ ,
здесь использованы формулы:
,
здесь использованы формулы:
 ,
,
 и
и

 ,
где
,
где
 при
при
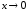 .
Имеем:
.
Имеем:

 .
Используя теорему о замене эквивалентными
в отношении, получим:
.
Используя теорему о замене эквивалентными
в отношении, получим:
 .
Таким образом, α(x)
является величиной более высокого
порядка малости, чем β(х)
при х→ 0,
.
Таким образом, α(x)
является величиной более высокого
порядка малости, чем β(х)
при х→ 0,
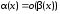 при х→ 0.◄
при х→ 0.◄
Пример
1.3. Сравнить
бесконечно малые α(x) и β(x)
и β(x) при
при
 .
.
►Имеем
α(x) ~
~ (здесь использована формула
(здесь использована формула
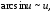 где
где
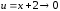 при
при
 ),
β(x)
),
β(x) =
= ~
~
~
~ ~
~ ,
(здесь использованы формулы:
,
(здесь использованы формулы:

 и
и
 ,
,
 ,
где
,
где
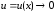 при
при
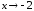 ).
Используя теорему о замене эквивалентными
в отношении, получим:
).
Используя теорему о замене эквивалентными
в отношении, получим:
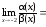
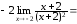
 .
Следовательно,
.
Следовательно,
 и поэтому заключаем, что β(x)
– величина более высокого порядка
малости, чем α(x)
при
и поэтому заключаем, что β(x)
– величина более высокого порядка
малости, чем α(x)
при
 ,
β(x) = o(α(x))
при
,
β(x) = o(α(x))
при
 .◄
.◄
Пример
1.4. Сравнить
бесконечно малые
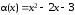 и
и
 при
при
 .
.
►Заметим,
что β(x)
не эквивалентна аргументу функции
sinπx,
который не является бесконечно малым
при
 .
Чтобы найти эквивалентную бесконечно
малую для этой функции, сделаем замену
переменной. Пусть y = x–3,
x = y + 3,
.
Чтобы найти эквивалентную бесконечно
малую для этой функции, сделаем замену
переменной. Пусть y = x–3,
x = y + 3,
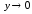 при
при
 .
Имеем:
.
Имеем:

 .
.
Так как sin(πy + 3π) = sin(πy + 2π + π) = sin(πy + π) = – sinπy, то

 =
=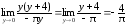 ,
,
здесь
использованы периодичность функции
синус, формулы приведения из элементарной
тригонометрии, а также соотношение
 где
где
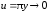 при
при
 .
Поскольку
.
Поскольку
 ,
то заключаем, что α(x)
и β(x)
бесконечно малые одного порядка при
,
то заключаем, что α(x)
и β(x)
бесконечно малые одного порядка при
 .◄
.◄
Пример
1.5. Сравнить
бесконечно малые α(x) и α(x)
и β(x)
и α(x)
и β(x)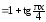 при
при
 .
.
►α(x) ~
~ ,
здесь использована формула
,
здесь использована формула
 где
где
 при
при
 .
Используя формулу для тангенса суммы
двух углов, преобразуем выражение для
β(x):
β(x) =
.
Используя формулу для тангенса суммы
двух углов, преобразуем выражение для
β(x):
β(x) = 
 Имеем:
Имеем:
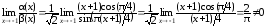 ,
∞, следовательно, α(x)
и β(x)
– бесконечно малые одного порядка при
,
∞, следовательно, α(x)
и β(x)
– бесконечно малые одного порядка при
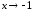 .◄
.◄
§ 2. Определение порядка бесконечно малой функции.
Определение
2.1. Пусть
функции α(x)
и β(x)
являются
бесконечно малыми при
 .
Бесконечно малая α(x)
называется бесконечно малой k-го
порядка по отношению к бесконечно малой
β(x)
при х
.
Бесконечно малая α(x)
называется бесконечно малой k-го
порядка по отношению к бесконечно малой
β(x)
при х а,
если существует
а,
если существует
 .
.
Так,
функция α(x) =sin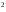 2x
имеет 2-ой порядок малости относительно
β(x) =х
(
2x
имеет 2-ой порядок малости относительно
β(x) =х
( )
при х
)
при х 0,
ибо
0,
ибо

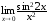
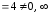 .
.
Определить
порядок малости бесконечно малой α(x)
относительно бесконечно малой β(x)
при х а
– значит найти число k
такое, чтобы
а
– значит найти число k
такое, чтобы
 .
При этом используется теорема о замене
эквивалентными в отношении и таблица
эквивалентных бесконечно малых функций
(§1), так как для α(x)
и β(x)
полезно найти эквивалентные бесконечно
малые вида С(х – а)k.
.
При этом используется теорема о замене
эквивалентными в отношении и таблица
эквивалентных бесконечно малых функций
(§1), так как для α(x)
и β(x)
полезно найти эквивалентные бесконечно
малые вида С(х – а)k.
Пример
2.1. Определить
порядок бесконечно малой α(x) .
относительно бесконечно малой β(x) = х
при
.
относительно бесконечно малой β(x) = х
при
 .
.
►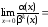
 (использованы
теорема о замене эквивалентными
бесконечно малыми в отношении и формулы:
(использованы
теорема о замене эквивалентными
бесконечно малыми в отношении и формулы:
 ,
,
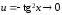 ,
,
 и
и

 при
при
 ).
Поскольку
).
Поскольку
 –
–
 при
при
 ,
то порядок малости α(x)
относительно β(x)
при х
,
то порядок малости α(x)
относительно β(x)
при х 0
равен 2.◄
0
равен 2.◄
Пример
2.2. Определить
порядок бесконечно малой α(x)
) =  относительно бесконечно малой β(x) = х
при
относительно бесконечно малой β(x) = х
при
 .
.
►
 (использованы
теорема о замене эквивалентными
бесконечно малыми в отношении и формула:
(использованы
теорема о замене эквивалентными
бесконечно малыми в отношении и формула:
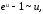
 при
при
 ).
Разложив числитель на множители, получим:
).
Разложив числитель на множители, получим:

 .
Поскольку
.
Поскольку
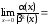 –3
–3 при
при
 ,
то порядок малости α(x)
относительно β(x)
при х
,
то порядок малости α(x)
относительно β(x)
при х 0
равен 2.◄
0
равен 2.◄
Пример
2.3. Определить
порядок бесконечно малой α(x) относительно бесконечно малой β(x) = х
при
относительно бесконечно малой β(x) = х
при
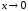 .
.
►
 .
Числитель разложим на множители по
формуле разность косинусов, получим:
.
Числитель разложим на множители по
формуле разность косинусов, получим:
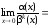
 .
После применения теоремы о замене
эквивалентными бесконечно малыми в
отношении и формулы:
.
После применения теоремы о замене
эквивалентными бесконечно малыми в
отношении и формулы:

 и
и
 при
при
 имеем:
имеем:

 .
Поскольку
.
Поскольку
 8
8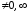 при
при
 ,
то порядок малости α(x)
относительно β(x)
при х
,
то порядок малости α(x)
относительно β(x)
при х 0
равен 2.◄
0
равен 2.◄
Пример
2.4. Определить
порядок бесконечно малой α(x)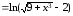 .
относительно бесконечно малой β(x) = х
при
.
относительно бесконечно малой β(x) = х
при
 .
.
►
 .
Числитель заменим на эквивалентную,
получим:
.
Числитель заменим на эквивалентную,
получим:

 (использована формула
(использована формула

 при
при
 ).
Перенесём иррациональность из числителя
в знаменатель, умножив оба члена дроби
на выражение, сопряжённое к числителю:
).
Перенесём иррациональность из числителя
в знаменатель, умножив оба члена дроби
на выражение, сопряжённое к числителю:
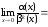
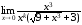 .
Поскольку
.
Поскольку


 при
при
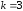 ,
то порядок малости α(x)
относительно β(x)
при х
,
то порядок малости α(x)
относительно β(x)
при х 0
равен 3.◄
0
равен 3.◄
Пример
2.5. Определить
порядок бесконечно малой α(x) =  относительно бесконечно малой β(x) = х – 1
при х
относительно бесконечно малой β(x) = х – 1
при х 1.
1.
►
 =
= =
=
 .
Так как
.
Так как
 1,
то
1,
то
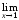
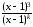 =1
=1 при
при
 .
Поэтому порядок малости α(x)
относительно β(x)
при х
.
Поэтому порядок малости α(x)
относительно β(x)
при х 1
равен 3.◄
1
равен 3.◄
Пример
2.6. Определить
порядок бесконечно малой α(x) = cos(πsinх) + 1
относительно бесконечно малой
β(x) = х – π/2
при
 .
.
►Для
α(x)
найдём эквивалентную бесконечно малую
вида С(х – π/2)k.
В результате применения формул для
половинных и дополнительных углов из
элементарной тригонометрии и формул


 из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
имеем соотношение:
из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
имеем соотношение:
α(x) =
 ~
~ ~
~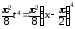 .
.
Итак,
α(x) ~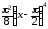 при
при
 .
Используя теорему о замене эквивалентными
в отношении, получаем:
.
Используя теорему о замене эквивалентными
в отношении, получаем:
 при
при

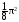
 при k
= 4. Таким образом, порядок малости α(x)
относительно β(x)
при х
при k
= 4. Таким образом, порядок малости α(x)
относительно β(x)
при х равен 4.◄
равен 4.◄
Пример
2.7. Определить
порядок бесконечно малой α(x) относительно бесконечно малой β(x) = х – π
при
относительно бесконечно малой β(x) = х – π
при
 .
.
►
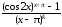 .
Используя основное логарифмическое
тождество, представим функцию
.
Используя основное логарифмическое
тождество, представим функцию
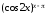 в виде:
в виде:
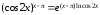 .
Имеем
.
Имеем
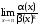 =
=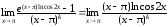 =
= =
=
 (использованы теорема о замене
эквивалентными бесконечно малыми в
отношении и формулы
(использованы теорема о замене
эквивалентными бесконечно малыми в
отношении и формулы

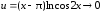 и
и

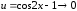 при
при
 .
Заметим, что разность
.
Заметим, что разность
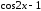 не эквивалентна
не эквивалентна
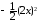 при
при
 ,
так как
,
так как
 не стремится к нулю при
не стремится к нулю при
 .
Чтобы найти для этой разности эквивалентную
бесконечно малую, сделаем замену
переменной: y = х – π
.
Чтобы найти для этой разности эквивалентную
бесконечно малую, сделаем замену
переменной: y = х – π x = y + π:
x = y + π:




 .
Поскольку
.
Поскольку
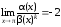
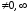 при
при
 ,
то порядок малости α(x)
относительно β(x)
при
,
то порядок малости α(x)
относительно β(x)
при
 равен 3.◄
равен 3.◄
§3. Выделение главной части бесконечно малой функции.
Определение
3.1. Пусть
даны функции α(x)
и β(x),
являющиеся
бесконечно малыми при х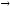 а.
Функция
а.
Функция
 называется главной частью функции α(x)
при х
называется главной частью функции α(x)
при х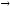 а,
если α(x)
при х
а,
если α(x)
при х а
можно
представить в виде:
а
можно
представить в виде:
α(x) = β(x) + o(β(x)). (3.1)
Если
бесконечно малые α(x)
и β(x)
эквивалентны при х а,
то для них справедливо равенство (3.1)
(свойство эквивалентных бесконечно
малых). Поэтому данная бесконечно малая
функция α(x)
при х
а,
то для них справедливо равенство (3.1)
(свойство эквивалентных бесконечно
малых). Поэтому данная бесконечно малая
функция α(x)
при х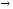 а
может иметь бесчисленное множество
главных частей, так как любая бесконечно
малая функция β(x),
эквивалентная α(x),
будет её главной частью. Например,
функции х,
tg x
– главные
части функции sin x
при х
а
может иметь бесчисленное множество
главных частей, так как любая бесконечно
малая функция β(x),
эквивалентная α(x),
будет её главной частью. Например,
функции х,
tg x
– главные
части функции sin x
при х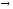 0,
так как при х
0,
так как при х 0
справедливы утверждения: sin x~x,
sin x~tg x.
0
справедливы утверждения: sin x~x,
sin x~tg x.
Обычно
главную часть функции α(x),
бесконечно малой при х а,
находят в
а,
находят в
наиболее
простом виде, например, в виде степенной
функции β(x) = С(х – а)k,
k > 0,
при a R
или
β(x) = С(1/х)k,
k > 0,
при a
R
или
β(x) = С(1/х)k,
k > 0,
при a .
Найти для α(x)
такую главную часть – значит определить
константу С
и порядок k
этой функции относительно разности
x – a
или дроби 1/х.
.
Найти для α(x)
такую главную часть – значит определить
константу С
и порядок k
этой функции относительно разности
x – a
или дроби 1/х.
Найти
для α(x)
главную часть простейшего вида С(х – а)k,
k > 0,
при х а
– это значит найти константу С
и число k
такие, чтобы
а
– это значит найти константу С
и число k
такие, чтобы
 .
.
Пример
3.1. Выделить
главную часть вида Схk
из бесконечно малой α(x) = cos2х – cos4х
при х  0.
0.
►В
результате применения формулы для
разности косинусов и формулы

 из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
имеем соотношение: α(x)
из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
имеем соотношение: α(x)
 .
Таким образом, для α(x)
найдена эквивалентная бесконечно малая
функция 6х2,
имеющая указанный вид (С = 6,
k = 2),
следовательно, 6х2.–
главная часть α(x)
при х
.
Таким образом, для α(x)
найдена эквивалентная бесконечно малая
функция 6х2,
имеющая указанный вид (С = 6,
k = 2),
следовательно, 6х2.–
главная часть α(x)
при х  0.◄
0.◄
Пример
3.2. Выделить
главную часть вида Схk
из бесконечно малой α(x) = при х
при х  0.
0.
► Найдём
число k
и константу С
такие, чтобы
выполнялось равенство:

 =1.
Перенесём иррациональность из числителя
в знаменатель, для этого умножим оба
члена дроби на выражение, сопряжённое
к числителю:
=1.
Перенесём иррациональность из числителя
в знаменатель, для этого умножим оба
члена дроби на выражение, сопряжённое
к числителю:

 =
=
 (использованы
теорема о замене эквивалентными
бесконечно малыми в отношении и формула:
(использованы
теорема о замене эквивалентными
бесконечно малыми в отношении и формула:

 при
при
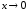 ).
Поскольку
).
Поскольку
 при k = 2
и
при k = 2
и
 ,
то
,
то
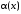 ~
~

 при х
при х  0
и, следовательно, функция
0
и, следовательно, функция

 – главная часть бесконечно малой α(x)
при х
– главная часть бесконечно малой α(x)
при х  0.◄
0.◄
Пример
3.3. Выделить
главную часть вида С(х – 2)k
из бесконечно малой α(x) при х
при х  2.
2.
►В
результате применения формулы

 из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
имеем соотношение:
из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
имеем соотношение:
α(x)
 .
.
Итак,
для α(x)
найдена эквивалентная бесконечно малая
функция 3(х– 1)2,
имеющая указанный вид (С = 3,
k = 2),
следовательно, 3(х–1)2–
главная часть α(x)
при х 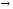 2.◄
2.◄
Пример
3.4. Выделить
главную часть вида С(х – 1)k
из бесконечно малой α(x) = cos(πex–1) + 1
при х 1.
1.
►В
результате применения формул для
половинных и дополнительных углов из
элементарной тригонометрии и формул
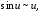

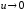 из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
имеем соотношение: α(x) = 2cos2
из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
имеем соотношение: α(x) = 2cos2
 = 2sin2
= 2sin2 2sin2
2sin2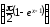
 .
.
Итак,
для α(x)
найдена эквивалентная бесконечно малая
функция
 ,
имеющая указанный вид (С =
,
имеющая указанный вид (С =  ,
k = 2),
следовательно,
,
k = 2),
следовательно,
 – главная часть α(x)
при х
– главная часть α(x)
при х  1.◄
1.◄
Пример
3.5. Выделить
главную часть вида С(1/х)k
из бесконечно малой α(x) = при х
при х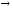
 .
.
► ,
α(x) =
,
α(x) = при х
при х
 (использована формула
(использована формула

 при х
при х
 ).
Имеем
).
Имеем


 при х
при х
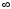 ,
отсюда заключаем:
,
отсюда заключаем:
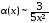 при х
при х
 ,
следовательно,
,
следовательно,
 – главная часть бесконечно малой α(x)
при х
– главная часть бесконечно малой α(x)
при х
 .◄
.◄
Пример
3.6. Выделить
главную часть вида С(х – e)k
из бесконечно малой α(x) = хx – ex
при х .
.
►Используя
основное логарифмическое тождество,
представим функцию хx
в виде:
хx = exlnx.
Имеем α(x) = exlnx – ex = ex(exlnx-х–1).
В результате применения
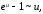
 из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
получаем соотношение:
из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
получаем соотношение:
α(x) ~ ее(х(lnx – 1)) = ее+1(lnx – lne) = ее+1 ~
~
при
х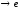 .
Итак, α(x) ~
.
Итак, α(x) ~  при х
при х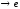 ,
Следовательно, ee (х–е)
– главная часть бесконечно малой α(x)
при х
,
Следовательно, ee (х–е)
– главная часть бесконечно малой α(x)
при х е.◄
е.◄
Пример
3.7. Выделить
главную часть вида Схk
из бесконечно малой α(x) = arccos(1 – x)
при х .
.
►Чтобы
найти для α(x)
эквивалентную бесконечно малую функцию
указанного вида, применим формулу

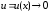 .
Имеем
.
Имеем
α(x) ~sin(arccos(1 – x))
при х .
.
Преобразуем
функцию sin(arccos(1 – x)),
Используя определение арккосинуса.
Пусть arccos(1 – x) = γ,
где γ – угол или дуга такая, что
cosγ = 1 – x
и
 ,
тогда sin(arccos(1 – x)) = sinγ =
,
тогда sin(arccos(1 – x)) = sinγ = 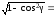
 .
Итак,
.
Итак,
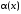 ~
~
 при
при
 и функция
и функция
 – главная часть бесконечно малой α(x)
при
– главная часть бесконечно малой α(x)
при
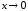 .◄
.◄
Пример
3.8. Выделить
главную часть вида
 из бесконечно малой α(x) = π – 4arctg(x2 – 2x + 2)
при х
из бесконечно малой α(x) = π – 4arctg(x2 – 2x + 2)
при х .
.
►α(x)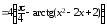 .
Для отыскания алгебраической функции,
эквивалентной α(x),
применим формулу
.
Для отыскания алгебраической функции,
эквивалентной α(x),
применим формулу

 ,
положив
,
положив
u = 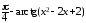 ,
а также формулу для разности тангенсов
двух углов из элементарной тригонометрии:
,
а также формулу для разности тангенсов
двух углов из элементарной тригонометрии:
α(x)
 .
.
Итак,
α(x) ~ – 2(x – 1)2
при
 и функция – 2(x – 1)2
– главная часть бесконечно малой α(x)
при
и функция – 2(x – 1)2
– главная часть бесконечно малой α(x)
при
 .◄
.◄
