
Хуета / с1.кр2-0
.docxСодержание контрольной работы №2
-
Неопределённость
 ,
отношение алгебраических функций.
,
отношение алгебраических функций. -
Неопределённость
 ,
отношение алгебраических функций.
,
отношение алгебраических функций. -
Неопределённость
 ,
отношение трансцентдентных функций.
,
отношение трансцентдентных функций. -
 .
Неопределённость
1∞.
.
Неопределённость
1∞. -
Сравнение бесконечно малых. Определение порядка одной бесконечно малой относительно другой. Выделение главной части бесконечно малой.
-
Исследование на непрерывность функции одной переменной.
Вариант 0
-
 .
. -
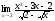 .
. -
 .
. -
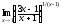 .
. -
Сравнить бесконечно малые
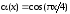 и
и
 при
при
 .
. -
Исследовать на непрерывность
 .
.
Решение варианта 0
-
Вычислить
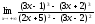 .
.
►
Так
как под знаком предела стоит отношение
двух многочленов, то разделим числитель
и знаменатель на старшую степень
аргумента, т. е. на
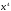 .
В результате получим
.
В результате получим

поскольку
при
 функции 3/x
и 9/x2
являются
бесконечно малыми. ◄
функции 3/x
и 9/x2
являются
бесконечно малыми. ◄
2).
Вычислить
 .
.
►Выражение
под знаком предела представляет собой
неопределённость
 в отношении алгебраических иррациональных
функций при х
в отношении алгебраических иррациональных
функций при х a,
a
a,
a R.
Метод раскрытия таких неопределённостей
состоит в перенесении иррациональности
из одного члена дроби в другой. В данном
случае перенесём иррациональность из
знаменателя дроби в числитель:
R.
Метод раскрытия таких неопределённостей
состоит в перенесении иррациональности
из одного члена дроби в другой. В данном
случае перенесём иррациональность из
знаменателя дроби в числитель:
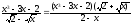 .
.
Многочлен

 разложим на множители, используя теорему:
“если число х
= а
разложим на множители, используя теорему:
“если число х
= а
является
корнем многочлена
 ,
то этот многочлен делится на разность
х –
а без
остатка”. Число х
= 2
– корень
многочлена
,
то этот многочлен делится на разность
х –
а без
остатка”. Число х
= 2
– корень
многочлена

 4,
поэтому он делится на разность х
– 2
без остатка.
Выполнив это деление, получим:
4,
поэтому он делится на разность х
– 2
без остатка.
Выполнив это деление, получим:

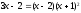 .
Таким образом,
.
Таким образом,
 ,
поэтому
,
поэтому
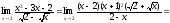
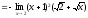 .
Здесь произведено деление обоих членов
дроби под знаком предела на разность х
– 2, поскольку
при вычислении предела х
принадлежит проколотой окрестности
точки х =
2 (т.е.
х ≠
2). Выражение из правой части последнего
равенства не даёт неопределённости при
х
.
Здесь произведено деление обоих членов
дроби под знаком предела на разность х
– 2, поскольку
при вычислении предела х
принадлежит проколотой окрестности
точки х =
2 (т.е.
х ≠
2). Выражение из правой части последнего
равенства не даёт неопределённости при
х 2,
его предел можно найти по теореме о
пределе суммы и произведения. Окончательно
получаем:
2,
его предел можно найти по теореме о
пределе суммы и произведения. Окончательно
получаем:
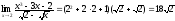 .◄
.◄
3).
Вычислить
 .
.
►Для
раскрытия получающейся здесь
неопределенности вида
 применяется теорема о замене эквивалентными
бесконечно малыми в отношении наряду
с использованием таблицы эквивалентных
бесконечно малых функций, следующей из
замечательных пределов.
применяется теорема о замене эквивалентными
бесконечно малыми в отношении наряду
с использованием таблицы эквивалентных
бесконечно малых функций, следующей из
замечательных пределов.
Таблица эквивалентных бесконечно малых функций.
Пусть
функция
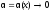 при
x →
а.
Тогда
при
x →
а.
Тогда




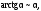


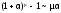 .
.
Так
как
 ,
,
 при
при
 ,
то в силу упомянутой теоремы находим
,
то в силу упомянутой теоремы находим
 .◄
.◄
4).
Найти
 .
.
► Функция
под знаком предела является
степенно-показательной и представляет
собой неопределённость
 ,
так как
,
так как
 ,
,
 .
С помощью основного логарифмического
тождества она может быть представлена
в виде:
.
С помощью основного логарифмического
тождества она может быть представлена
в виде:
 .
.
В силу свойства непрерывности показательной функции на R имеем равенство:
 .
.
Таким
образом, задача сведена к вычислению
предела:
 .
С помощью основного логарифмического
тождества и свойства непрерывности
показательной функции неопределённость
.
С помощью основного логарифмического
тождества и свойства непрерывности
показательной функции неопределённость
 трансформирована в неопределённость
трансформирована в неопределённость
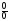 ,
которую, после некоторых преобразований,
раскроем с помощью теоремы о замене
эквивалентными в отношении и сотношения:
,
которую, после некоторых преобразований,
раскроем с помощью теоремы о замене
эквивалентными в отношении и сотношения:
 при
при
 .
Имеем
.
Имеем

 и
и
 =
е.◄
=
е.◄
5)
Сравнить бесконечно малые
 и
и
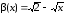 при
при
 .
.
►

-
поэтому α(x) и β(x) бесконечно малые одного порядка при
 .
.
6. Исследовать на непрерывность следующие функции:
1)
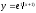 ;
2)
;
2)

►1) Данная функция определена при всех действительных значениях х, кроме х = ± 1. На каждом из промежутков, входящих в область определения функция она является элементарной и, следовательно, непрерывной по теореме о непрерывности элементарной функции. В точках х = ± 1 функция терпит разрыв непрерывности. Для классификации разрывов, рассмотрим односторонние пределы данной функции в этих точках:
 ,
так как 1/(x+1) → – ∞
при х→ – 1 – 0;
,
так как 1/(x+1) → – ∞
при х→ – 1 – 0;
 ,
так как 1/(x+1) → + ∞
при х→ – 1 + 0.
Итак, один из односторонних пределов в
точке х = – 1
является бесконечным, поэтому в этой
точке функция имеет разрыв второго
рода.
,
так как 1/(x+1) → + ∞
при х→ – 1 + 0.
Итак, один из односторонних пределов в
точке х = – 1
является бесконечным, поэтому в этой
точке функция имеет разрыв второго
рода.
2) Данная функция определена на всей вещественной оси, на каждом из промежутков
(– ∞,1), (1, 4), (4, + ∞) она задана как элементарная и, следовательно, является непрерывной. “Подозрительными на разрыв” являются точки, в которых изменяется аналитическое выражение функции, т. е. точки х = 1 и х = 4. Вычислим односторонние пределы в этих точках.
Для точки х = 1 имеем:
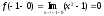 ;
;
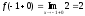 .
.
Односторонние пределы функции в точке х = 1 существуют, но не равны между собой, поэтому эта точка является точкой разрыва первого рода.
Для точки х = 4 получаем
 .
.
Односторонние
пределы функции при
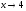 равны между собой и равны частному
значению функции:
равны между собой и равны частному
значению функции:
 .
Следовательно, исследуемая точка
является точкой непрерывности. ◄
.
Следовательно, исследуемая точка
является точкой непрерывности. ◄
