
DZ-Razdel_4-2017
.docРаздел 4. ВВЕДЕНИЕ В АНАЛИЗ
Задание 4-1. (Построение графиков простейших элементарных функций.)
Постройте графики функций, укажите область определения и множество значений функций:
4-1.1. а) y ln(x 4); б) y 1 e2x; в) ![]() ; г)
; г) ![]() ;
д) y x3.
;
д) y x3.
4-1.2. а) y | x 1|; б) y | ln x |; в) y ln | x 5 |.
Задание 4-2. (Нахождение пределов без применения правила Лопиталя.)
Найдите пределы:
-
а)О
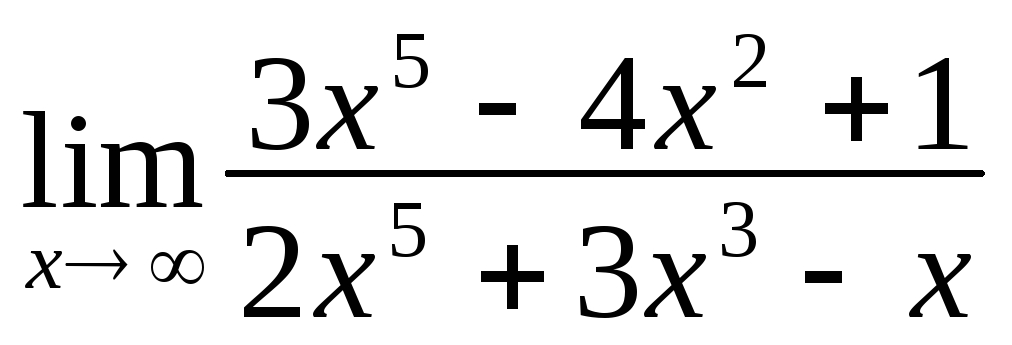 ;
б) О
;
б) О
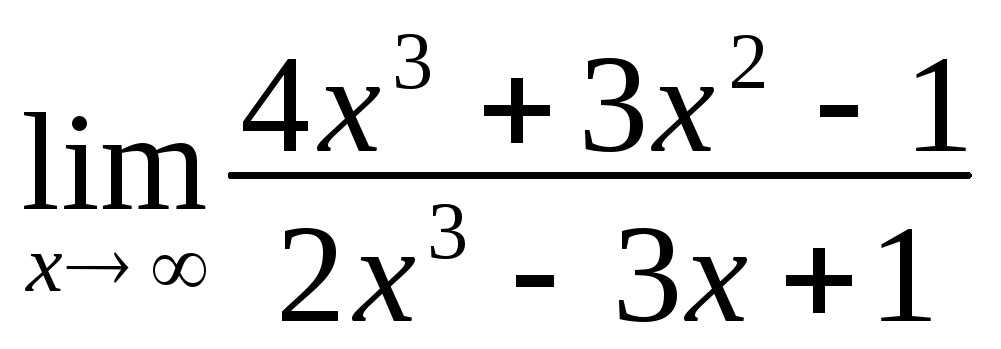 .
.
в)
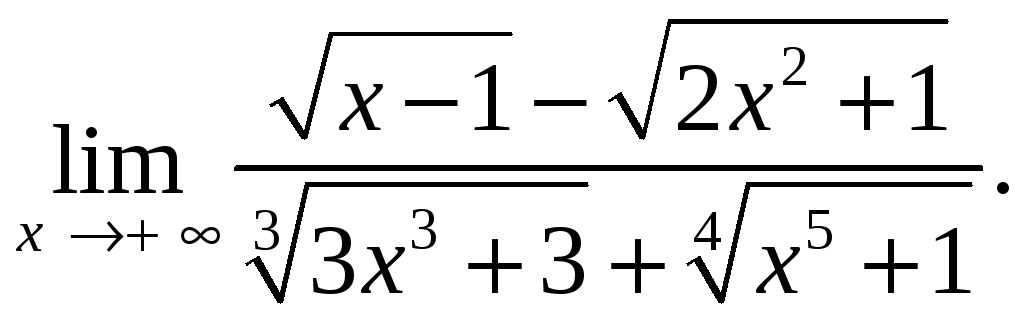
-
а)О
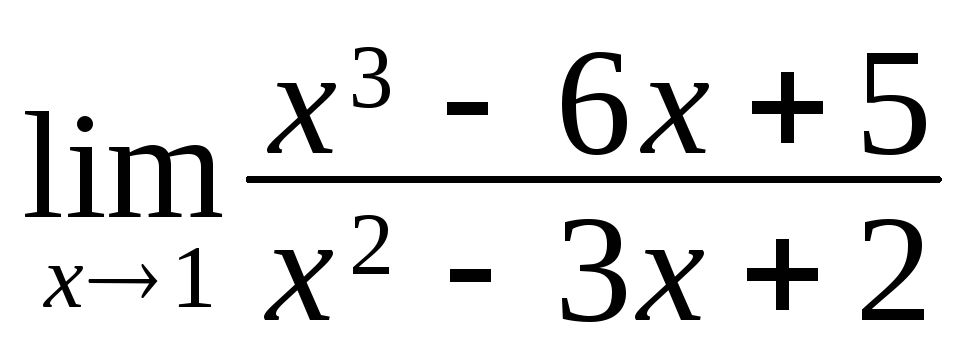 ;
; 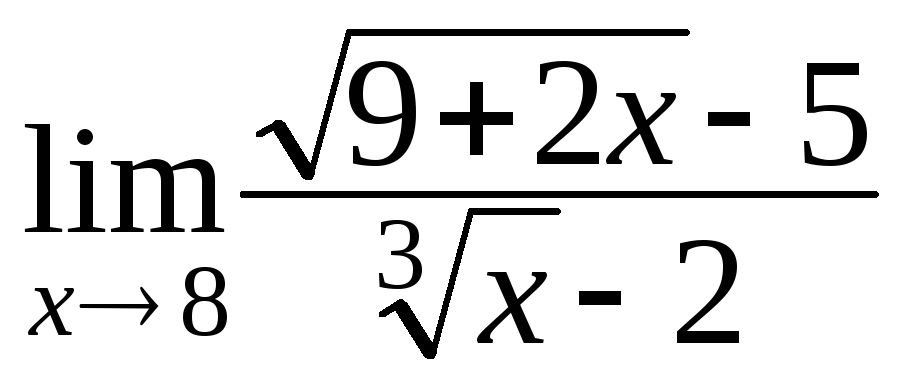
б)О
![]() .
.
![]() .
.
4-2.3. а)О
![]() ;
; ![]() ;
; ![]()
б) О![]() ;
; ![]() ;
; ![]()
4-2.4. а)О
![]() ; б)
О
; б)
О
![]() .
.
Задание
4-3. Cравнить
бесконечно малые функции
α(x)
и β(x)
при
![]() :
:
|
4-3.1. а)О
α(x) = |
β(x) = |
|
|
б)О
|
|
|
|
4-3.2. а)О α(x) = lncosx, |
β(x) = x3 – 2x, |
|
|
б)Оα(x) = cos(x – 2) –1, |
|
|
|
4-3.3. а)О α(x) = arctg(x + 1), |
β(x) = |
|
|
б)О
|
β(x) = 1 – cos(x + 2), |
|
Задание
4-4. Определить
порядок малости бесконечно малой
![]() относительно
бесконечно малой
относительно
бесконечно малой
![]() при
при
![]() .
.
|
4-4.1.
а)О
|
б)О
|
|
4-4.2.
а)О
|
б)О
|
|
4-4.3.
а)О
|
б)О.
|
Задание 4-5. Выделить главную часть
вида
![]() из бесконечно малой
из бесконечно малой
![]() при
при
![]() .
.
|
4-5.1.
а)О
|
б)О
|
|
4-5.2.
а)О
|
б)О
|
Задание 4-6. Найдите
точки разрыва функции
![]() и
определите характер разрыва.
и
определите характер разрыва.
4-6.1. а)О
![]()
![]() ;
б)О
;
б)О
![]()
![]() .
.
4-6.2. а)О
![]()
![]() ; б)
О
; б)
О![]()
![]() .
.
4-6.3. а)О
![]()
![]() ; б)
О
; б)
О
![]()
![]() .
.
Ответы
4-2.1. а)О 3/2. б)О 2. 4-2.2. а)О 4. б)О – 4. в) 0.4-2.3. а)О 3. б)О 6/5. 4-2.4. а)О 12/5. б)О 4/3.
4-2.5. а)О 8/3; 5/3; 1/2; б)О 2; –3; –2. 4-2.6. а)О e–3; б)О e6.
4-3.1. а)О функции
![]() и β(x) одного порядка;
б)О функции
и β(x) одного порядка;
б)О функции
![]() и β(x) одного порядка.
и β(x) одного порядка.
4-3.2. а)О
![]() =о(β(x));
б)О
=о(β(x));
б)О
![]() =о(β(x)).
4-3.3. а)О β(x)
=о(
=о(β(x)).
4-3.3. а)О β(x)
=о(![]() );
б)О β(x)
=о(
);
б)О β(x)
=о(![]() ).
).
4-4.1. а)О 2. б)О 2. 4-4.2. а)О 3. б)О 3. 4-4.3. а)О 2. б)О 1.
4-5.1. а)О –x2/2.
б)О
![]() .
4-5.2. а)О –x3/3;
б)О x3.
.
4-5.2. а)О –x3/3;
б)О x3.
