3.4.Поляризация волн

3.4.1.Естественный и поляризованный свет. Форма и степень поляризации монохроматических волн

Поляризованным называется свет, в котором направления колебаний светового вектора упорядочены каким-либо образом. В естественном свете колебания различных направлений быстро и беспорядочно сменяют друг друга.

Рассмотрим два взаимно перпендикулярных электрических колебания, совершающихся вдоль осей х и у, и отличающихся по фазе на :

Результирующая напряженность , угол между векторами и определяется выражением

Если считать световые волны когерентными, и =0 или =. Тогда – волна оказывается плоскополяризованной.

Если и , тогда - плоскость колебаний поворачивается вокруг направления луча с угловой скоростью, равной частоте колебаний . Свет оказывается поляризованным по кругу.

В случае произвольного значения  свет оказывается эллиптически поляризованным, конец вектора движется по эллипсу.

Плоскость, в которой колеблется световой вектор в плоскополяризованной волне, называют плоскостью колебаний. Перпендикулярная к ней плоскость называется плоскостью поляризации.

Плоскополяризованный свет можно получить из естественного с помощью поляризаторов. Это приборы, которые свободно пропускают колебания, параллельные плоскости поляризатора, и полностью или частично задерживают колебания, перпендикулярные его плоскости. Поляризатор, частично задерживающий перпендикулярные к его плоскости колебания, называют несовершенным. При выходе из такого поляризатора свет называют частично поляризованным.

Если частично поляризованный свет пропустить через поляризатор и поворачивать прибор вокруг луча на угол , интенсивность прошедшего света будет меняться от до . Степень поляризации света

Для плоскополяризованного света , для естественного света

Пусть на поляризатор падает плоскополяризованный свет амплитуды и интенсивности .

Сквозь прибор пройдет составляющая колебания с амплитудой , где  - угол между плоскостью колебаний падающего света и плоскостью поляризатора. Тогда интенсивность прошедшего света

Это закон Малюса.

Если на пути луча поставить два поляризатора, плоскости которых образуют угол , то из первого поляризатора выйдет плоскополяризованный свет с интенсивностью , где - интенсивность естественного света, а из второго поляризатора выйдет свет с интенсивностью , и интенсивность света, прошедшего через оба поляризатора, равна

Imax= , Imin=0, .

3.4.2. Отражение и преломление света на границе раздела двух диэлектриков. Формулы Френеля. Полное отражение и его применение в технике. Волноводы и световоды. Брюстеровское отражение

О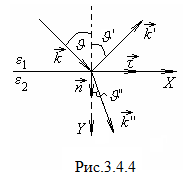 тражение и преломление волнового вектора на границе двух диэлектриков даёт плоская электромагнитная волна, которая попадает на плоскую границу раздела двух однородных и изотропных диэлектриков с проницаемостями и (рис.3.4.4). Магнитные проницаемости полагаем равными единице. Кроме распространяющейся во втором диэлектрике плоской преломлённой волны , возникает плоская отражённая волна, распространяющаяся в первом диэлектрике . На границе двух диэлектриков должно выполняться условие

, (3.4.1 )

где и - тангенциальные составляющие напряжённости электрического поля в первой и во второй среде соответственно.

, определяющий направление распространения падающей волны, лежит в плоскости чертежа (рис.3.4.4). Направ­ление нормали к поверхности раздела охарактеризуем вектором . Плоскость, в которой лежат векторы и , называется плоскостью падения волны. Возьмем линию пересечения плоско­сти падения с границей раздела диэлектриков в качестве оси . Ось направим перпендикулярно к плоскости раздела диэлектри­ков. Тогда ось будет перпендикулярна к плоскости падения, а вектор окажется направленным вдоль оси (рис.3.4.4). Из соображений симметрии ясно, что век­торы и могут лежать лишь в плоскости падения (среды однородны и изотропны).

Колеба­ния вектора в плоской электромагнитной волне, распространяю­щейся в направлении вектора , описываются функцией

Напряженности в отраженной и преломленной волнах опреде­ляются аналогичными выражениями:

,

( и - начальные фазы соответствующих волн).

Показанные на рис. 3.4.2 углы _и называются углом падения, углом отражения и углом преломления.

.

и = ; = ;

.

Отсюда вытекает, что

, ( 3.4.4 )

Закон отражения света, согласно которому отраженный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; угол отражения равен углу падения.

. ( 3.4.5 )

Закон преломления света, который формулируется следующим образом: преломлен­ный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения;

Величина называется относительным показателем преломления второго ве­щества по отношению к первому.

.

закон преломления в виде

.

при переходе света из оптически более плотной среды в оптически менее плотную луч удаляется от нор­мали к поверхности раздела сред. Увеличение угла падения со­провождается более быстрым ростом угла преломления , и по достижении углом значения

Предельный угол.

Энергия, которую несет с собой падающий луч, распределяется между отраженным и преломленным лучами. По мере увеличения угла падения интенсивность отраженного луча растет, интенсивность же преломленного луча убывает, обращаясь в нуль при предельном угле. При углах падения, заключенных в пределах от до , световая волна проникает во вторую среду на расстояние порядка длины волны и затем возвращается в первую среду. Это явление называется полным внутренним отражением.

Обозначим электрическую составляющую в падающей, отраженной и преломленной волнах соответственно через , и , а магнитную составляющую через , и .

колебания векторов и происходят вдоль того же направления, что и колебания вектора . Аналогично колебания векторов и происходят вдоль направления вектора .

В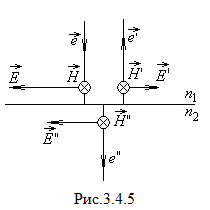 данном случае нормальные составляющие векторов и равны нулю. Поэтому тангенциальные составляющие этих векторов совпадают с самими векторами. Модули векторов и связаны соотношением _. Тройка вектора , , образует правовинтовую систему:

. (3.4.6 )

Аналогичные соотношения имеют место и для векторов в отраженной и преломленной волнах.

Условия непрерывности тангенциальных составляю­щих векторов и

, ( 3.4.7 )

. ( 3.4.8 )

Заменив в ( 3.4.8 ) векторы векторами и

.

Векторы и взаимно перпендикулярны, тогда

. ( 3.4.9 )

Решив совместно уравнения ( 3.4.7 ) и ( 3.4.9 ), получим

, ( 3.4.10)

. ( 3.4.11 )

Подставив в выражение значения (3.4.10 ) и ( 3.4.11 ) для и

.

Это соотношение получено для мгновенных значений . Аналогич­ное соотношение имеет место и для амплитудных значений свето­вого вектора:

. ( 3.4.12 )

выражает закон сохранения энергии.

Коэффициент отражения и коэффициент пропускания световой волны

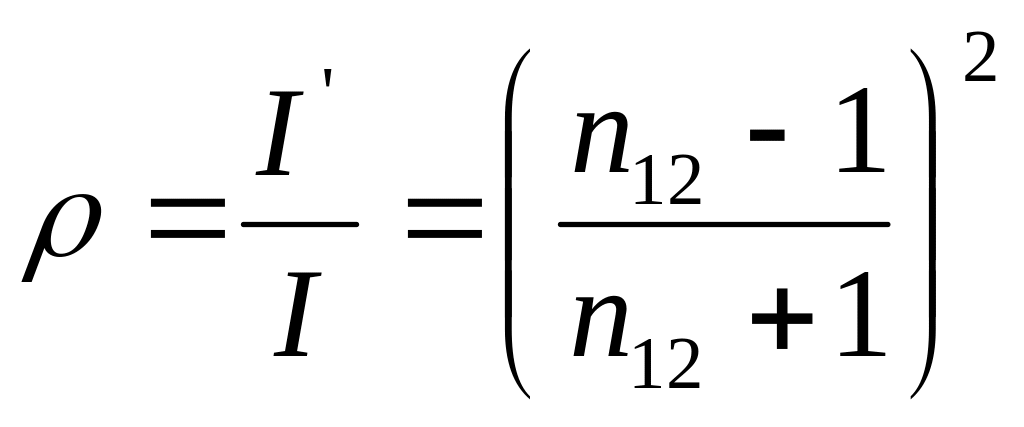, ( 3.4.13 )

где - показатель преломления второй среды по отно­шению к первой.

Для коэффициента пропускания получается выражение

.

, (3.4.14)

Закон Брюстера

отраженный луч полностью поляризован, он содержит только колебания, перпендикулярные плоскости падения. Степень поляризации при угле падения достигает наибольшего значения, однако преломленный луч остается частично поляризованным. угол - угол Брюстера.

при произвольном угле падения и соответствующем ему угле преломления коэффициенты отражения линейно-поляризованного света, плоскость поляризации которого перпендикулярна плоскости падения ( ) и параллельна ей ( ), определяются выражениями :

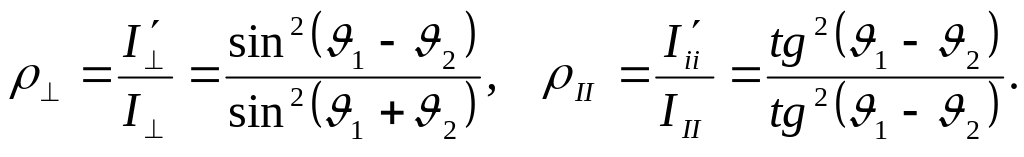
При падении под углом Брюстера и коэффициент отражения , т.е. отраженный свет будет полностью линейно поляризован в плоскости, перпендикулярной плоскости падения.

Явление полного отражения света лежит в основе принципа действия волноводов и световодов. Волновод – это устройство или канал в неоднородной среде, вдоль которого могут распространяться направленные волны. Различают экранированные волноводы , образованные зеркально отражающими стенками, а также системы, в которых поперечная локализация волн обусловлена полным внутренним отражением.

Световод (оптический волновод) – это закрытое устройство для направленной передачи света. В открытом пространстве его передача возможна только в пределах прямой видимости и связана с потерями, Переход к световодам позволяет значительно уменьшить потери световой энергии при ее передаче на большие расстояния, а также передавать световую энергию по криволинейным трассам.

Наибольшее распространение получили волновые световоды. Такой световод представляет собой тонкую нить из оптически прозрачного материала, сердцевина которой радиуса а₁ имеет показатель преломления п₁, а внешняя оболочка с радиусом а₂ имеет показатель преломления . Поэтому лучи, распространяющиеся под достаточно малыми углами к оси световода, испытывают полное внутреннее отражение на поверхности раздела сердцевины и оболочки и распространяются только по сердцевине.

Луч распространяется в положительном направлении оси Z вблизи оси расстояние от оси Z обозначим r. Запишем закон преломления света на бесконечно тонком слое , в котором показатель преломления изменяется от n(r ) до n(r+ ):

.

.

Поскольку , в параксиальном приближении можно записать:

.

Тогда уравнение распространения луча: