Расчет геометрических характеристик плоских сечений

Задание :

1. Определить положение центра тяжести сечения.

2. Провести главные центральные оси поперечного сечения.

3. Вычислить главные центральные моменты инерции поперечного сечения.

4. Вычислить главные центральные и радиусы.

Решение

СЕЧЕНИЕ I

1. Определяем положение центра тяжести сечения.

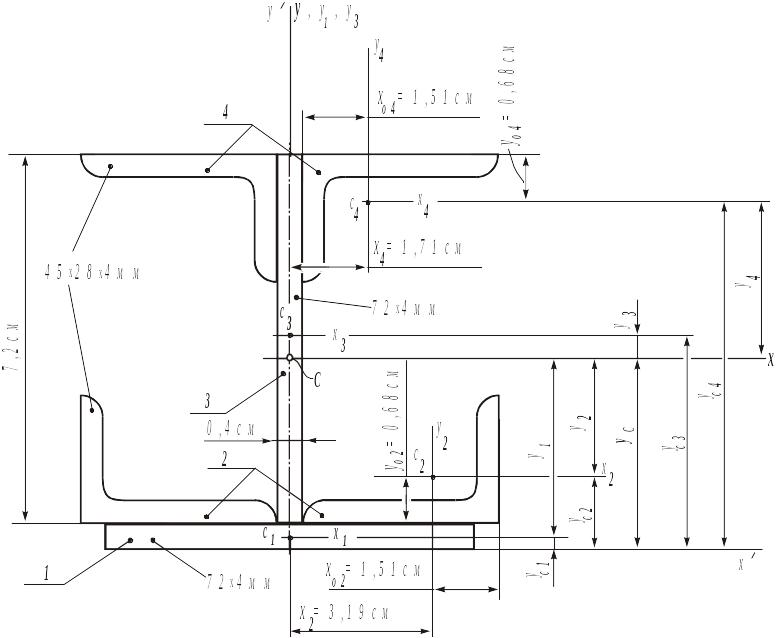
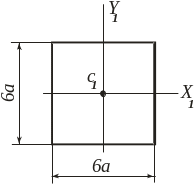
1.1. Изобразим сечение I в масштабе (рис. 17).

Рис. 17. Расчетная схема сечения I

Выберем исходные (вспомогательные) оси и . Ось проходит через нижние точки сечения, ось совпадает с осью симметрии сечения.

Сечение состоит из двух прямоугольников (   ) и четырех неравнобоких уголков (   ).

1.2. Вычисляем геометрические характеристики простых фигур, составляющих заданное сечение.

1) Прямоугольник (   ):

;   ;   .

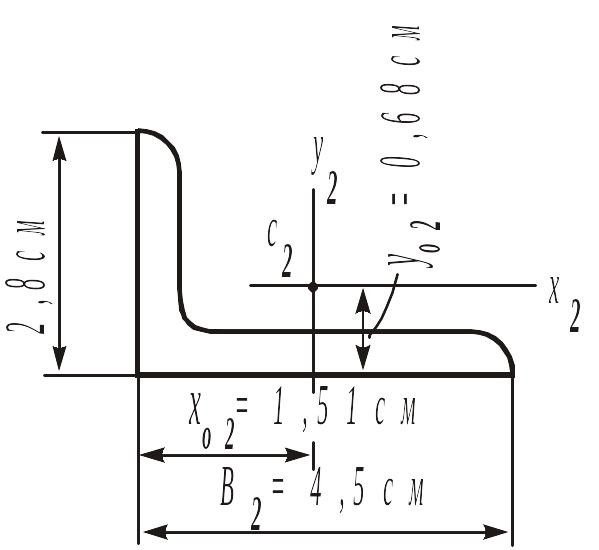
2, 4) Неравнобокие уголки (   ):

;   ;   ;   ;   .

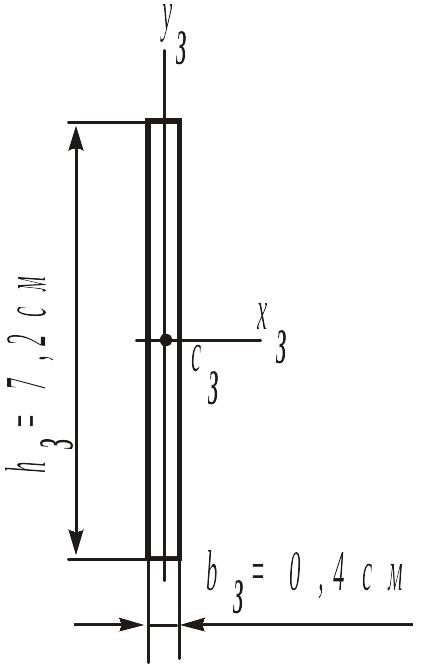
3) Прямоугольник ( ):

;   ;   .

1.3. Определяем положение центра тяжести заданного сечения.

Заданное сечение имеет одну ось симметрии, которая является главной центральной.

Координата центра тяжести сечения определяется по формуле:

,

где - расстояние между вспомогательной и центральной осью простого сечения:

  ;

  ;

  ;

  .

Тогда

  ,

здесь

  .

2. Проводим главные центральные оси поперечного сечения.

На оси , на высоте от вспомогательной оси , находится центр тяжести всего сечения. Главная центральная ось параллельна вспомогательной оси и проходит через центр тяжести всего сечения С.

3. Вычисляем главные центральные моменты инерции сечения.

;

.

Координаты центров тяжести простых сечений относительно главных центральных осей определяем по рис. 17:

  ;

  ;

  ;

  ;

;

  ;

  .

После подстановки числовых значений, получим:

  ;

  .

4. Вычисляем главные центральные радиусы инерции.

  ;

  .

СЕЧЕНИЕ 2

1. Определяем положение центра тяжести сечения.

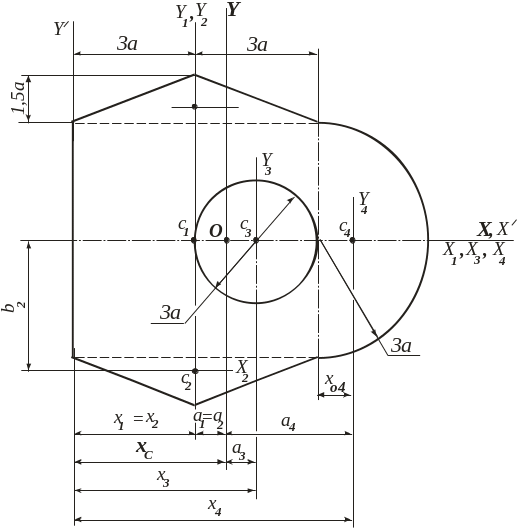
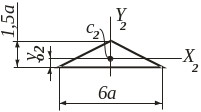
1.1. Изобразим сечение с одной осью симметрии в масштабе.

Выбираем исходные оси , . Ось проходит по левому краю сечения, ось совпадает с осью симметрии сечения.

Сечение состоит из квадрата , двух треугольников , круглого отверстия ( ) и полукруга ( ).

1.2. Вычисляем собственные геометрические характеристики элементов, составляющих сечение.

	1) Квадрат ( ): ; ; .
	2) Треугольники ( ): ; ; ; .
	3) Круглое отверстие ( ): ; ; .
	4) Полукруг ( ): ; ; ; .

Площадь сечения.

.

1.3. Определяем положение центра тяжести заданного сечения.

Заданное сечение имеет одну ось симметрии, которая является главной центральной.

Координата центра тяжести сечения определяется по формуле:

, где

;

;

;

.

Тогда

;

  .

2. Проводим главные центральные оси поперечного сечения.

Центр тяжести сечения находится на оси , на расстоянии от вспомогательной оси . Главная центральная ось параллельна вспомогательной оси и проходит через центр тяжести всего сечения О.