51-1
По
теореме Ферма производная
в
точке минимума функции f
равна
Ответ:
0 (ноль)
51-2
По
правилу Лопиталя, если f
(a)
=
g(a)
=
0
и существуют
и
,
причем
0,
то
Ответ:
=
51-3
Если
функция f
дифференцируема
на (a,b)
и
>0
на
(a,b),
то
функция f
на
(a,b)
Ответ:
Строго возрастает
51-4
Если
=0,
а
<0,
то в точке x0
функция f
Ответ:
Функция f имеет максимум
51-5
Установить соответствие
Ответ:
Параметры уравнения наклонной асимптоты y = kx + b
Формулы для вычисления k и b
1.
k
– В.
2. b – Д. [f(x) – k*x]
51-6
Формулировка теоремы Ролля такова ____________________________. Доказательство.
Ответ:
Если
функция
f
непрерывна на [a,b],
дифференцируема на (a,b)
и f(a)=f(b),
тогда
C
(a,b),
где
(с)=0
Доказательство:
Е(f)=[m;M]
m=
f
M=
f
1)
Если
m=M => f(x)=m=const
x
(a,b)
(x)=0 x (a,b)
2) Если m<M
Т.к. f(a)=f(b), то хотя бы одно из этих значений достигается внутри интервала (a,b). Пусть f(C)=M, C (a,b) => (с)=0
51-7
По
правилу Лопиталя
равен
Ответ:
=
=
=
=(0*
)=
=(
)=
=
=(
)=
=(
)=
=1
51-8
Для
функции y=
52-1
Установить соответствие
Ответ:
Характер критической точки x0
Необходимые условия
1. Экстремум – В. (x0) = 0
2.
Перегиб
– Д.
(x0)
=
0
52-2
По
правилу Лопиталя, если функции f
и
g
дифференцируемы
при х
> с,
f(x)=
,
g(x)=
,
g(x)
0
при х
> с и
существует
,
тогда
Ответ:
=
52-3
Если функция f дифференцируема на (a,b) и (x) <0 на (a,b), то функция f на (a,b)
Ответ:
Строго убывает
52-4
Если (x)<0 для x (a,b), то функция f на (a,b)
Ответ:
Выпукла вверх
52-5
Если
y
=
kx
+
b
-
асимптота функции f
при
x
,
то k
равно
Ответ:
k=
52-6
Формулировка теоремы о достаточных условиях выпуклости вверх (вниз) кривой такова: ________________________. Доказательство
Ответ:
Если
(x)
(
)
0
x
(a,b),
f
C[a,b]
(непрерывна), то функция f
выпукла вниз f
(выпукла
вверх f
)
Доказательство:
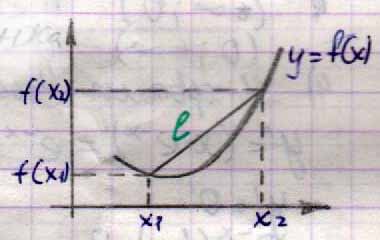
L:
y=
f(x)-
=
-
=
=
f(x)-f(x2)=- (c0)(x2-x)
f(x)-f(x1)= (c1)(x-x1)
=
=
=
52-7
По
правилу Лопиталя
равен
Ответ:
=
=
=
=
=
=
=
=
=
=1
52-8
Для
функции
y=x*
53-1
По теореме Ролля, если функция f непрерывна на [a,b], дифференцируема на (a,b) и f (a) = f (b) , то
Ответ:
С (a,b), где (C)=0
53-2
Если функция f дифференцируема в окрестности точки x0 , =0 и производная (x)<0 при x<x0; (x)>0 при x > x0 , то
Ответ:
-
точка минимума
53-3
По
правилу Лопиталя, если функции f
и
g
дифференцируемы
на (a,b),
f(x)=
g(x)=0
и g(x)
0
для
x
(a,b),
то
Ответ:
=
53-4
Если (x) >0 для x (a,b), то функция f на (a,b) является
Ответ:
Выпуклой вниз
53-5
Установить соответствие
Ответ:
Уравнение асимптот для функции y = f (x)
Необходимые и достаточные условия
1.
x
=
a
– Г.
f(x)=
2. y = b – В. f(x)=b
53-6
Формулировка теоремы Ферма такова _____________________________. Доказательство
Ответ:
Если функция f достигает максимума (минимума) в точке х0 и дифференцируема в точке в точке х0, то (х0)=0
Доказательство:
(x0-
;x0+
):
f(x0)>f(x)
при x
(x0-
;x0)
(x0;x0+
)
(х0)=
0
(х0)=
0
=>
=> (х0)=0
53-7
По
правилу Лопиталя
равен
Ответ:
=(
)=
=
=
=(
)=
=
=
=
=
=
=
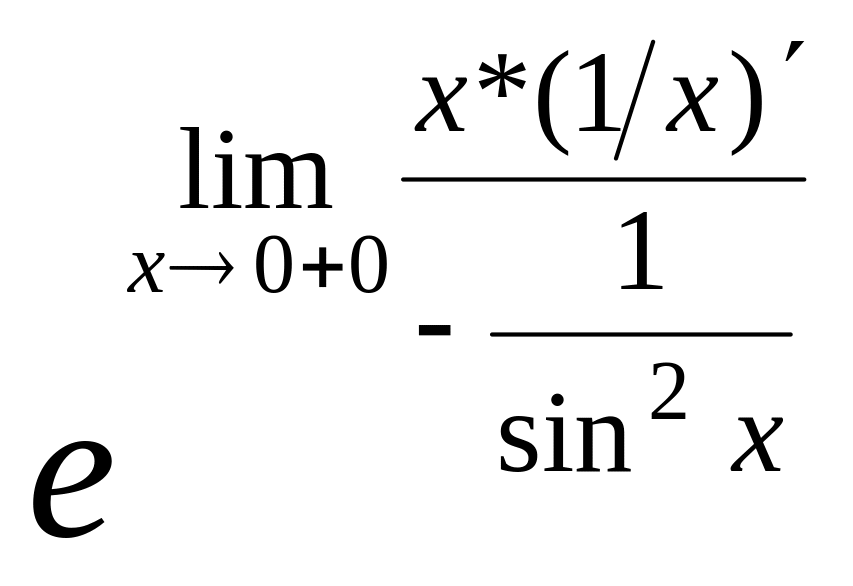=1
53-8
Для
функции
y=
54-1
По теореме Лангранжа, если функция f непрерывна на [a,b], и дифференцируема на (a,b), то
Ответ:
С (a,b): f(b)-f(a)= (C)(b-a)
54-2
Установить соответствие для дифференцируемой функции y = f (x), x (a,b)
Ответ:
Значения (x) на (a,b)
Функция y = f (x) на (a,b)
1. Положительны - Е. Возрастает
2. Отрицательны - С. Убывает
54-3
Если функция f дифференцируема в окрестности точки x0 , и производная (x)>0 при x<x0; (x)<0 при x>x0, то
Ответ:
- точка максимума
54-4
Если точка x0 является точкой перегиба функции f и существует (x) в окрестностях точки x0, то (x0)
Ответ:
(x0)=0
54-5
По определению, функция f называется выпуклой вниз на [a,b], если
Ответ:
f(a(альфа, здесь и далее)x1+(1-a)x2) af(x1)+(1-a)f(x2)
x1,x2 [a,b], a [0;1]
54-6
Формулировка теоремы о первом достаточном условии существования экстремума функции ___________. Доказательство
54-7
По
правилу Лопиталя предел
равен
Ответ:
=(
)=
=
=
=
=
=
=
54-8
Для
функции
y=2x+
55-1
По теореме Коши, если функции f и g непрерывны на [a,b], дифференцируемы на (a,b) и g(x) 0 для любого x (a,b), то
Ответ:
C
(a,b):
=
55-2
По правилу Лопиталя, если функции f и g дифференцируемы на (a,b), f(x)= , g(x)= , g(x) 0 на (a;b) и существует то
Ответ:
=
55-3
Установить соответствие для дважды дифференцируемой функции y = f (x), x (a,b), =0, x0 (a,b)
Ответ:
Значения
x0 есть точка
1. Положительно - Г. Минимума
2. Отрицательно - А. Максимума
55-4
Если
(x)
меняет
знак при переходе через точку x0
, причем
=0,
то для функции f
(x)
точка x0
является
Ответ:
- точка перегиба
55-5
По определению функция f (x) называется выпуклой вверх на (a,b), если
Ответ:
f(a(альфа, здесь и далее)x1+(1-a)x2) af(x1)+(1-a)f(x2)
x1,x2 [a,b], a [0;1]
55-6
Формулировка теоремы Лагранжа такова ____________________________. Доказательство
Ответ:
Пусть функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема на отрезке (а,b), то с (a,b): f(b)-f(a)=f(c)(b-a)