Транспортная задача

Представим транспортную задачу по критерию стоимости в виде таблицы

Поставщики	ПОТРЕБИТЕЛИ				Запас груза
	B1	B2	…	Bn
А1	X11 c11	X12 c12	…	X1n c1n		a1
…	…					…
Аm	…					an
Потребность в грузе	b1

В таблице указаны поставщики А1… , у которых имеется в наличии соответственно а₁… единиц однородного груза. Данный груз должен быть доставлен n потребителям, в количествах в₁… единиц, заданы стоимости с_ij перевозок груза от i поставщика j потребителю. Требуется спланировать перевозки(указать, сколько единиц груза должно быть отправлено от I того поставщика j потребителю, так чтобы максимально удовлетворить спрос потребителя и чтобы суммарные затрата на перевозки были при этом минимальными).

c₁ – цена.

Задачи, где суммарные запасы грузов поставщиков равны суммарным потребностям, называются закрытыми.

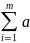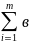_I != _I – то задача открытая.

При решении транспортных задач важное значение имеет теорема о ранге матрицы:

Ранг матрицы транспортной задачи на 1 меньше числа уравнений(r=m+n-1).

Столько должно быть занятых иксами клеток в транспортной задаче. Решение транспортной задачи проводится с помощью общего приема последовательного улучшения плана, что включает этапы:

1.Определение исходного опорного плана.

2.Оценка этого плана.

3.Переход к следующему плану путем однократной замены одной из базисных переменных на свободную.

Существуют различные способы реализации этапов решения транспортной задачи:

1.Правило северо-западного угла.

Пример:

Поставщики	ПОТРЕБИТЕЛИ				Запас груза
	B1	B2	B3	B4
А1	4 \ 40	3 \10	2 \-	6 \ -		50
A2	2 \-	4 \50	5 \20	1 \ -		70
А3	3 \-	6 \-	7 \30	5 \70		100
Потребность в грузе	40	60	50	70

2.Правило минимального элемента.

Пример:

Поставщики	ПОТРЕБИТЕЛИ				Запас груза
	B1	B2	B3	B4
А1	4 -	3 0	2 50	6 -		50
A2	2 0	4 -	5 -	1 70		70
А3	3 40	6 60	7 -	5 -		100
Потребность в грузе	40	60	50	70