Вопросы для самопроверки
Какими физическими процессами можно описать электрические колебания, возникающие в контуре?
Сформулируйте уравнения затухающих и вынужденных колебаний в контуре.
Как определить разность фаз между током в контуре и внешней э. д. с.?
Что такое векторная диаграмма напряжений и токов? Какой вид она имеет при вынужденных колебаниях в RLC - контуре?
Определите резонансные частоты тока и напряжения на емкости при резонансе.
Сформулируйте понятия логарифмического декремента затухания и добротности контура. Как связаны данные величины между собой?
Перечислите последовательность обработки результатов эксперимента и порядок выполнения работы.
Лабораторная работа 4 Эффект Холла
Цель работы: изучение эффекта Холла в полупроводнике; исследование зависимости э. д. с. Холла от напряженности внешнего магнитного поля (градуировка датчика Холла); определение постоянной Холла, концентрации и подвижности носителей заряда в полупроводнике; исследование распределения магнитного поля по оси короткого соленоида; сравнение с теоретической зависимостью.
ОСНОВНЫЕ ПОНЯТИЯ.
Эффектом
Холла называется явление возникновения
поперечной разности потенциалов в
металле или полупроводнике между точками
на прямой, перпендикулярной вектору
индукции магнитного поля
и направлению вектора плотности тока
.
Поперечная разность потенциалов
обусловлена магнитной составляющей
силы Лоренца, действующей на движущийся
со скоростью
заряд:
(6.1)
Рассмотрим
действие магнитного поля на полупроводник
по которому течет ток. Пусть полупроводник
имеет форму параллелепипеда сечением
и длиной a.
Электрическое поле направим вдоль оси
x,
магнитное поле вдоль оси y.
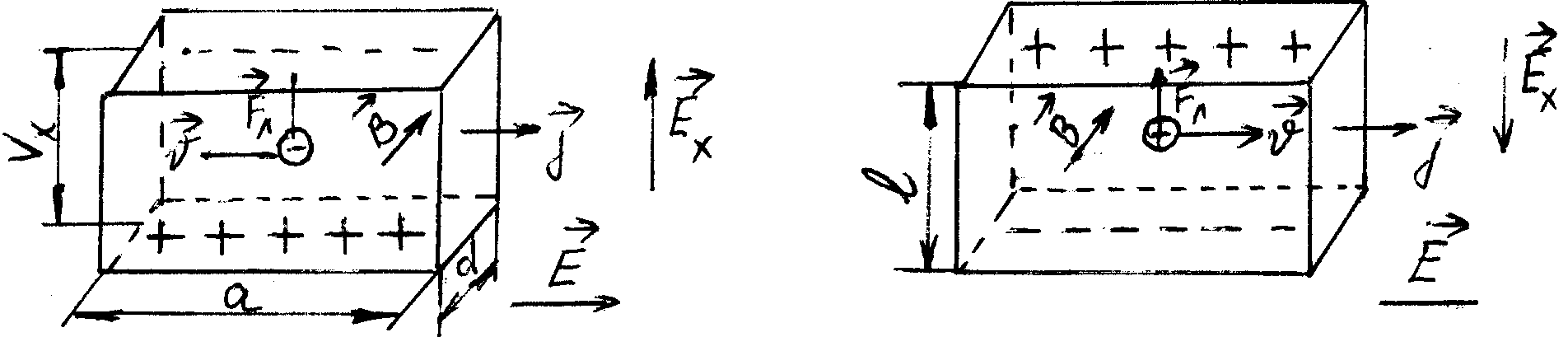
а) б)
Рис 6.1
При включении электрического поля в полупроводнике протекает ток с плотностью
(6.2)
где s - коэффициент электропроводности.
Под
действием электрического поля носители
заряда получают скорость направленного
движения
- дрейфовую скорость - против поля для
электронов (Рис.6.1 а) и по полю для дырок
(Рис.6.1 б). При включении магнитного поля
на электроны и дырки действует сила
,
определяемая выражением (6.1), перпендикулярная
и
.
Из уравнения движения носителей заряда
следует, что за время t
между двумя соударениями электроны и
дырки приобретают скорость
(6.3)
С учетом (6.3), получаем для силы F выражение
,
(6.4)
из
которого следует, что сила Лоренца не
зависит от знака носителей заряда и
действует в направлении перпендикулярном
и
(6.4).
В
результате действия силы отрицательные
заряды отклоняются к верхней грани, а
на нижней появляется их недостаток -
положительный заряд (Рис.6.1 а). Аналогично
осуществляется перераспределение
положительных зарядов (Рис.6.1 б).
Противоположные грани образца заряжаются
и возникает электрическое поле. Это
поле носит название поля Холла. Направление
поля Холла
зависит от знака носителей заряда. До
наложения на образец магнитного поля
эквипотенциальные поверхности
представляли плоскости, перпендикулярные
вектору
.
Величина
будет расти до тех пор, пока поперечное
поле не скомпенсирует силу Лоренца
(6.4). После этого носители заряда будут
двигаться как бы под действием одного
поля
,
и траектория движения будет представлять
собой прямую линию вдоль оси x.
Суммарное электрическое поле
будет повернуто на некоторый угол j
относительно оси x
или y.
Таким
образом в ограниченном полупроводнике
или металле поворачивается вектор
электрического поля и между
и
возникает угол j,
называемый углом Холла. Эквипотенциальные
поверхности при этом повернуты на угол
j
относительно их первоначального
положения, поэтому в точках, лежащих в
одной плоскости, перпендикулярной
появляется разность потенциалов
,
которая называется холловской разностью
потенциалов.
Холл экспериментально определил, что зависит от плотности тока, индукции магнитного поля и свойств образца. Свойства образца определяются некоторой величиной R, называемой коэффициентом Холла. Четыре величины , , и R связаны эмпирическим соотношением:
(6.5)
Коэффициент Холла или постоянная Холла определяется из условия равенства сил:
(6.6)
Из (6.6) следует, что
,
(6.7)
где
- подвижность носителей заряда.
В соответствии с (6.5), напряженность поля Холла можно определить в виде:
.
(6.8)
Сопоставляя (6.7) и (6.8) видим, что
,
(6.9)
где n - концентрация носителей заряда в единице объема. Из (6.9) следует, что постоянная Холла обратно пропорциональна концентрации носителей заряда и ее знак совпадает со знаком носителей заряда. Поле Холла (6.8) приводит к появлению э. д. с. Холла Vx, которая с учетом выражения (6.9) и геометрических размеров имеет вид:
,
(6.10)
где
- ток через датчик.
В реальном кристалле полупроводника носители рассеиваются на примесях и колебаниях решетки. Учет данных процессов для полупроводников с собственной а) и примесной б) проводимостью приводит к следующему выражению для R:
а)
,
б)
,
(6.11)
где
e
- заряд электрона,
,
- подвижности электронов и дырок, n
и p
- их концентрации. Знак постоянной Холла
позволяет определить тип преимущественной
проводимости полупроводника.