Методика эксперимента

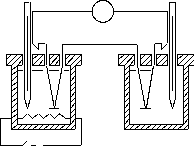
П. нагрев. - охлаждение 1 2 3

Горячие спаи

Рис.2.6

В установке используют термопарный термометр, состоящий из батареи М последовательно соединенных холодных и горячих спаев двух разнородных металлов (рис.2.6). Горячие 1 спаи помещены в сосуд с водой 3, нагреваемый элементом 4. Температура воды регистрируется термометром 5. Холодные спаи 2 помещены в сосуд с водой 6 при комнатной температуре, регистрируемой термометром 7. Так как горячие и холодные спаи одинаковы то по формуле (2.7) для последовательного соединения 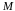спаев перепишется так:

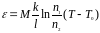
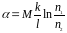
где 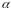- постоянная термопары.

При включении нагревателя температура горячих спаев увеличивается и по цепи с милливольтметром потечет ток. В процессе измерения регистрируется линейная зависимость () термоэлектродвижущей силы от разности температур горячего и холодного спаев. Как следует из (2.9) тангенс угла наклона 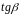прямой 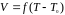к оси абцисс равен постоянной термопары , то есть

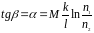(2.10), откуда 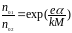(2.11)

Обработка результатов эксперимента

1. Построить зависимость термоэлектродвижущей силы от разности температур горячего и холодного спаев, провести через точки прямую

2. По формуле () найти отношение концентрации электронов в металлах спая термопары.

РАСЧЕТ ПОГРЕШНОСТЕЙ.

1. Вычисление постоянной термопары по зависимости 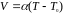и случайной погрешности 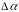осуществляется по методу наименьших квадратов (см). При этом уравнение линейной регрессии имеет вид:

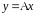
где - угловой коэффициент наклона прямой, проходящей через начало координат. Этот коэффициент находится по формуле:

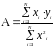, здесь

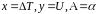
Погрешность определения углового коэффициента 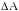находится из соотношения:

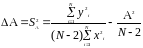
Приборная погрешность определения складывается из систематических погрешностей измерения термоэдс и температуры и на основании зависимости 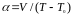вычисляется по формуле:

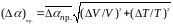
где 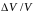- класс точности вольтметра, 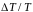- относительная погрешность измерения температуры. Величина 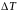определяется по цене деления амперметра, пересчитанной в градусах.

Суммирование систематической и случайной погрешностей осуществляется по формуле () и дает:

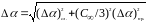
Рабочая формула для расчета отношения концентрации носителей:

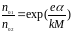
Расчет погрешности 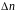осуществляется как расчет погрешности косвенного измерения (), в результате чего получается формула:

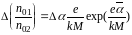
Вопросы для самопроверки

Что такое работа выхода электронов из металла?

Что такое внутренняя и внешняя контактные разности потенциалов?

В каком случае возникает термо-э. д. с. и отчего она зависит?

Что такое удельная термоэ. д. с.?

Выведите формулу для определения удельной термоэ. д. с.

В чем заключается градуировка термопары?

Выведите формулу для определения погрешности в измерении?

Лабораторная работа 2 Индуктивность

Цель работы: изучение закона электромагнитной индукции, расчет индуктивности короткого соленоида; проверка закона Ома для цепи постоянного и переменного тока с индуктивностью и активным сопротивлением; экспериментальное определение индуктивности короткого соленоида и магнитной проницаемости сердечника.

ОСНОВНЫЕ ПОНЯТИЯ.

1. При любом изменении магнитного потока через поверхность, ограниченную проводящим контуром, между точками 1 и 2 проводника возникает электродвижущая сила индукции, численно равная скорости изменения магнитного потока (закон Фарадея):

(3.1)

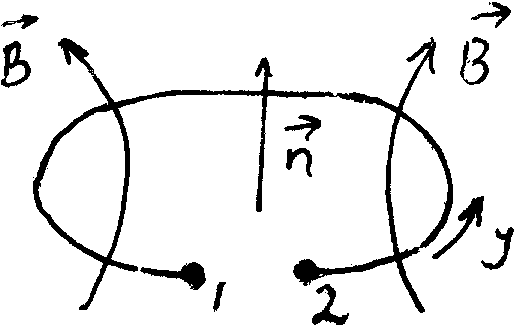
Рис.3.1

Из уравнения (3.1) следует, что поток магнитной индукции может изменяться как при движении контура в стационарном магнитном поле, так и за счет изменения индукции магнитного поля во времени. Знак минус выражает правило Ленца: ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот ток.

В отсутствии внешнего магнитного поля электрический ток: текущий в контуре: создает вокруг себя магнитное поле: индукция которого по закону Био-Савара-Лапласа пропорциональна току в контуре. Если в контуре протекает переменный ток, то сцепленный с ним магнитный поток будет изменяться во времени и между точками 1 и 2 возникает э. д. с. индукции. Данное явление называется самоиндукцией. Магнитный поток при самоиндукции пропорционален току в контуре

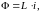(3.2)

так что закон Фарадея можно записать в следующей форме:

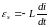(3.3)

Коэффициент пропорциональности L называется индуктивностью контура и зависит только от его геометрических размеров. Индуктивность определяется из закона Био-Савара-Лапласа в результате интегрирования по длине проводящего контура l с учетом выражения (3.2) для потока магнитной индукции:

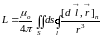, (3.4)

где 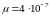Гн/м - магнитная проницаемость вакуума, 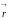- радиус-вектор: проведенный из элемента контура 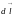в элемент 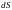поверхности S, ограниченной данным контуром, индекс "n" означает проекцию векторного произведения на нормаль к поверхности.

2. Получим формулу для расчета индуктивности короткого соленоида, длина которого l соизмерима с его радиусом 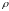(рис.3.2).

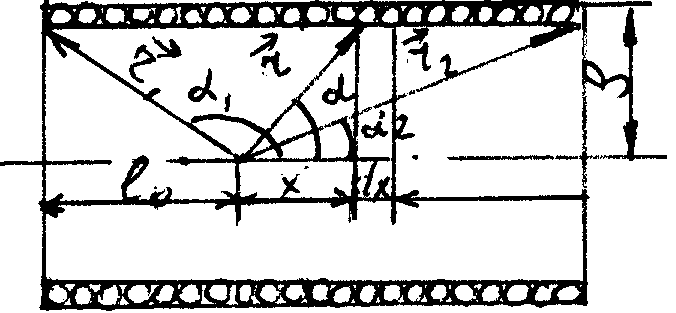
Рис.3.2

Индукция магнитного поля в точке 0 на оси соленоида, создаваемая участком намотки 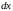пропорциональна числу витков на данной длине:

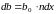, (3.5)

где 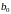- индукция, создаваемая одним витком, - число витков на единице длины. В соответствии с законом Био-Савара-Лапласа ток, протекающий в элементе 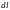проводящего контура, создает в точке 0 индукцию

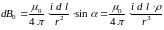(3.6)

Интегрируя уравнение (3.6) по длине витка, получаем выражение для индукции магнитного поля, создаваемую одним витком:

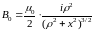(3.7)

В результате интегрирования уравнения (3.5) по всем значениям в интервале от до - 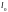и замены переменных 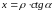, получаем следующее выражение для индукции магнитного поля на оси соленоида:

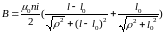(3.8)

При вычислении индукции магнитного поля реального соленоида необходимо учитывать не только зависимость 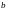от , но и неоднородность поля по сечению соленоида. Для расчета индуктивности короткого соленоида, магнитная индукция которого зависит от его сечения, можно использовать приближенную формулу:

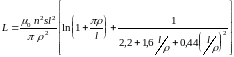(3.9)

Для длинного соленоида ( >> ) формула (3.9) существенно упрощается и имеет следующий вид:

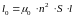(3.10)

Индуктивность катушки, заполненной магнетиком с магнитной проницаемостью, рассчитывается по формулам:

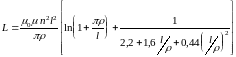(3.11)

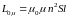(3.12)

3. Определим величину переменного тока в цепи, состоящей из катушки индуктивности с активным сопротивлением 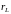, подключенной к источнику переменного напряжения .

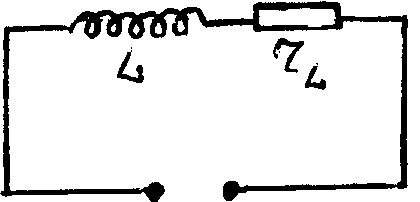
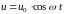
Рис.3.3

В соответствии с формулами (4.11) и (4.12) этот ток изменяется по закону

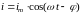(3.13)

Амплитуда тока 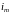и фаза определяются амплитудой, параметрами цепи 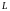, 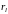и частотой w:

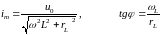(3.14)

Из (3.14) следует, что ток в цепи отстает по фазе от приложенного напряжения на угол 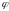, который зависит от параметров цепи и частоты:

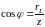, (3.15), где

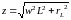- полное электрическое сопротивление цепи.

Зависимость амплитуды тока от выражает закон Ома для цепи переменного тока. Если w=0, то по цепи течет постоянный ток, для которого

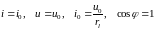(3.16)