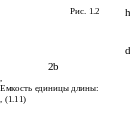- •Введение
- •Лабораторная работа 1 Термоэлектродвижущая сила
- •Методика эксперимента
- •Обработка результатов эксперимента
- •Вопросы для самопроверки
- •Лабораторная работа 2 Индуктивность
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов эксперимента
- •Расчет погрешностей
- •Вопросы для самопроверки
- •Лабораторная работа 3.
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов эксперимента
- •Расчет погрешностей
- •Вопросы для самопроверки
- •Лабораторная работа 4 Эффект Холла
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов эксперимента
- •Расчет погрешностей
- •Вопросы для самопроверки
- •Лабораторная работа 4. Изучение свойств феромагнетиков
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов эксперимента
- •Расчёт погрешностей
- •Вопросы для самопроверки
- •Лабораторная работа 5. Электростатическое поле
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов эксперимента
- •Расчет погрешностей
- •Вопросы для самопроверки
Расчёт погрешностей
Расчет погрешности определения величин остаточной индукции и коэрцитивной силы находятся как приборные погрешности косвенных изменений с учетом рабочих формул:
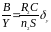 и
и
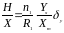 ,
,
где
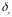 масштабный
коэффициент по вертикальной оси.
масштабный
коэффициент по вертикальной оси.
Так как
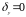 ,
,
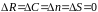 ,
то
,
то
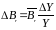 ,
,
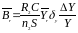
где
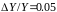 - погрешность определения амплитуды
осциллографом в нормальных условиях
эксплуатации.
- погрешность определения амплитуды
осциллографом в нормальных условиях
эксплуатации.
Аналогично на основании () получим:
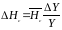 ,
,
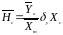
Вопросы для самопроверки
Что такое магнитный момент атома?
Объясните намагничивание диамагнетиков.
Объясните намагничивание парамагнетиков.
Что называется напряженностью магнитного поля?
Что такое магнитная восприимчивость и проницаемость магнетика и как магнетики классифицируются
В чем состоит явление магнитного гистерезиса у ферромагнетиков по величине магнитной проницаемости и восприимчивости? и как оно объясняется с помощью теории доменов? Опишите методику эксперимента.
Как по построенному чертежу петли гистерезиса определить остаточную индукцию, коэрцитивную силу и потери на перемагничивание?
Как рассчитываются погрешности эксперимента?
Лабораторная работа 5. Электростатическое поле
Цель работы: изучение основных свойств и характеристик электростатического поля и метода его моделирования; построение силовых линий и эквипотенциалей плоского поля в заданной системе электродов; изучение взаимосвязи между потенциалом и напряженностью; экспериментальное определение ёмкости системы электродов и распределения поля между ними.
ОСНОВНЫЕ ПОНЯТИЯ.
Электрический заряд создает вокруг себя электрическое поле и через поле осуществляет взаимодействие с другими зарядами. Между зарядами действуют кулоновские силы величина и направление которых зависит от формы и размеров наэлектризованных тел и характера распределения зарядов на них. Для точечных электрических зарядов кулоновская сила взаимодействия имеет вид:
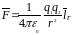 ,
(1.1)
,
(1.1)
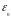 =10
/36p
Ф/м - диэлектрическая постоянная,
=10
/36p
Ф/м - диэлектрическая постоянная,
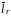 - единичный вектор направления. В каждой
точке пространства электрическое поле
характеризуется напряженностью Е и
потенциалом.
- единичный вектор направления. В каждой
точке пространства электрическое поле
характеризуется напряженностью Е и
потенциалом.
Напряженностью электростатического поля в данной точке называется векторная величина, численно равная отношению силы, действующей в данной точке на пробный заряд (т.е. точечный заряд достаточно малый, чтобы не искажать исследуемое поле) к величине этого заряда;
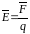 ,
(1.2)
,
(1.2)
Направление вектора напряженности совпадает с направлением силы, действующей на положительный пробный заряд
Напряженность поля является силовой характеристикой электростатического поля. Единица измерения напряженности вольт на метр (В/м)
Линией напряженности (силовой линией) является кривая, касательная к которой в каждой точке совпадает с вектором Е. Силовые линии электростатического поля начинаются и заканчиваются на зарядах или на бесконечности. С помощью линий напряженности удобно изображать поле графически. В расположении и форме этих линий сказывается все особенности данного поля.
Потенциалом поля в данной точке называется скалярная величина, численно равная отношению потенциальной энергии пробного заряда в указанной точке к величине этого заряда
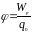 ,
(1.3)
,
(1.3)
За единицу потенциала принят один вольт (В=1Дж/Кл)
Точки постоянного потенциала образуют в пространстве эквипотенциальные поверхности.
Эквипотенциальные поверхности в однородной среде всегда перпендикулярны силовым линиям. Связь между потенциалом и напряженностью задается в виде:
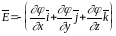 ,
(1.4)
,
(1.4)
где
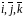 - орты декартовой системы координат,
- орты декартовой системы координат,
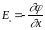 ,
,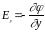 ,
,
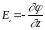
т.е. каждая декартовая составляющая вектора Е численно равна изменению потенциала на единицу длины, отсчитанному в направлении, перпендикулярном эквипотенциальной поверхности, и направлена в сторону убывания потенциала.
Выражение
(1.4) называется градиентом потенциала
и обозначается кратко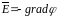 .
.
В силу потенциальности электростатического поля работа по перемещению заряда не зависит от формы пути, а определяется только положением начальной и конечной точки траектории.
В электростатическом поле выполняется принцип суперпозиции полей
Пример: точечный заряд
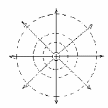
Рис.1.1
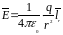 (1.5),
(1.5),
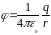 (1.6)
(1.6)
Сообщенный
проводнику заряд
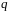 распределяется на его поверхности таким
образом чтобы напряженность поля внутри
проводника равнялась нулю. Потенциал
уединенного проводника пропорционален
величине заряда
распределяется на его поверхности таким
образом чтобы напряженность поля внутри
проводника равнялась нулю. Потенциал
уединенного проводника пропорционален
величине заряда
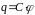 ,
(1.7)
,
(1.7)
Величина
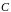 называется электрической емкостью
проводника. При приближении к проводнику
других проводников на них появляются
наведенные заряды (это явление называется
электростатической индукцией) и потенциал
уменьшается, емкость возрастает. Система
проводников называется конденсатором,
собственно проводники - обкладками.
называется электрической емкостью
проводника. При приближении к проводнику
других проводников на них появляются
наведенные заряды (это явление называется
электростатической индукцией) и потенциал
уменьшается, емкость возрастает. Система
проводников называется конденсатором,
собственно проводники - обкладками.
Величина емкости конденсатора зависит от разности потенциалов между обкладками:
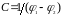 ,
(1.8)
,
(1.8)
и определяется формой, размером обкладок и расстоянием между ними.
Примеры
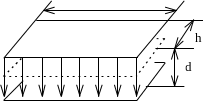
а) Плоский конденсатор. Поле однородно без учета краевых эффектов при d<<a,h
|
|
|
|
б
0 2b
) Распределение поля вдоль оси ОХ
a h d Ёмкость
единицы длины
|
|
в) Распределение поля вдоль оси ОХ
Рис.1.2
|
Электростатическое поле в диэлектрике подобно полю постоянного тока в проводящей среде при одинаковой конфигурации электродов. Если потенциалы электродов в обоих случаях одни и те же, распределение потенциала в диэлектрике такое же, как и в проводящей среде с током.
Подобие полей видно из следующего сопоставления теорем Гаусса и для электростатического поля и уравнения непрерывности для квазистационарного тока
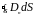
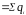 ,
(1.12)
,
(1.12)
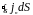
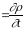 (1.13)
(1.13)
В
которых
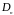 - нормальная составляющая к замкнутой
поверхности
- нормальная составляющая к замкнутой
поверхности
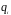 - заряды внутри поверхности,
- заряды внутри поверхности,
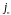 - нормальная к замкнутой поверхности
составляющая плотности тока,
- нормальная к замкнутой поверхности
составляющая плотности тока,
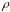 - объемная плотность заряда в проводнике.
- объемная плотность заряда в проводнике.
Если
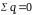 и
и
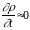 (медленно меняющийся ток),
(медленно меняющийся ток),
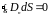 ,
(1.14)
,
(1.14)
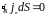 ,
(1.15)
,
(1.15)
Имеется подобие и между граничными условиями. На границе раздела диэлектриков тангенциальная и нормальная составляющие вектора напряженности электрического поля подчиняются условиям
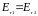 ;
;
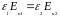
В проводящей среде непрерывность тангенциальных составляющих следует из потенциальности поля тока. Граничные условия для нормальных составляющих вектора плотности тока
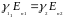
следуют
из уравнения непрерывности
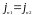
Из
подобия граничных условий следует, что
проводящая среда с током может служить
моделью для исследования электростатического
поля, если проводимость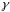 среды заменить диэлектрической
проницаемостью
,
заданной для моделируемого диэлектрика,
а электроды в обоих случаях расположить
одинаково. Поле в неоднородном диэлектрике,
различные области которого имеют
неодинаковую диэлектрическую
проницаемость, можно также моделировать
на проводящей среде, если подобны
распределения
и
.
Измерить распределение потенциала в
проводящей среде проще, чем в диэлектрике,
поэтому исследование на модели зачастую
предпочтительнее, чем на электростатическом
оригинале. Одной из задач электростатики,
которая может быть решена с помощью
моделирования, является определение
емкости. Емкость
исследуемой системы можно найти, измерив
распределение потенциала в проводящей
модели и вычислив его градиент
(напряженность поля Е).
Расчетная
формула для емкости
среды заменить диэлектрической
проницаемостью
,
заданной для моделируемого диэлектрика,
а электроды в обоих случаях расположить
одинаково. Поле в неоднородном диэлектрике,
различные области которого имеют
неодинаковую диэлектрическую
проницаемость, можно также моделировать
на проводящей среде, если подобны
распределения
и
.
Измерить распределение потенциала в
проводящей среде проще, чем в диэлектрике,
поэтому исследование на модели зачастую
предпочтительнее, чем на электростатическом
оригинале. Одной из задач электростатики,
которая может быть решена с помощью
моделирования, является определение
емкости. Емкость
исследуемой системы можно найти, измерив
распределение потенциала в проводящей
модели и вычислив его градиент
(напряженность поля Е).
Расчетная
формула для емкости
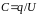 получается,
если в определении емкости заменить
заряд, по теореме Гаусса, потоком вектора
электрического смещения через замкнутую
поверхность:
получается,
если в определении емкости заменить
заряд, по теореме Гаусса, потоком вектора
электрического смещения через замкнутую
поверхность:
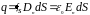 ,
(1.16)
,
(1.16)
Тогда емкость
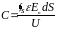 ,
(1.17)
,
(1.17)
Поток
вычисляют по замкнутой эквипотенциальной
поверхности, охватывающей электрод
моделируемой системы, с использованием
найденных на проводящей модели значений
нормальной компоненты вектора
напряженности
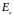 .
Разность
потенциалов
берется равной
напряжению между электродами модели,
диэлектрическая проницаемость - значению,
заданному для моделируемого диэлектрика.
.
Разность
потенциалов
берется равной
напряжению между электродами модели,
диэлектрическая проницаемость - значению,
заданному для моделируемого диэлектрика.

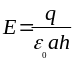 ,
,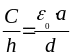 ,
(1.9)
,
(1.9)
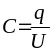
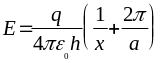 ,
(1.10)
,
(1.10) 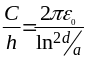 ,
(1.11)
,
(1.11)