Лабораторная работа №6

Исследование линейной разветвленной электрической цепи синусоидального тока

Цель работы и задачи работы

Исследовать явление резонанса токов, установить условия возникновения резонанса ,зависимости тока и параметров цепи от частоты напряжения питания, получить навыки построения векторных диаграмм и их использования для анализа электрических цепей.

Теоретические сведения, необходимые для выполнения лабораторной работы

Разветвленная электрическая цепь подключенная к сети синусо­идального тока, состоящая из сопротивления включённого последовательно с цепочкой параллельно соединенных катушки индуктивности и кон­денсатора представлена на рис.1а.

В отличие от задачи анализа процессов в электрической цепи с последовательно включенными элементами в схеме замещения параллельных ветвей удобнее воспользоваться параллельной схемой замещения катушки индуктивности с активной проводимостью G и реактивной индуктивной проводимостью B_L (рис.1б). Конденсатор представляется реактивной емкостной проводимостью В_C.

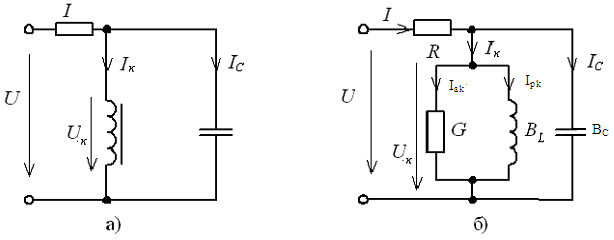
Рисунок 1 –Схемы электрической цепи: а) электрическая принципиальная, б) схема замещения

Проведём анализ электрического состояния параллельно включённых ветвей (рис.1б). Активная и реактивная проводимости катушки и конденсатора связаны с сопротивлениями соотношениями:

В соответствии с законом Ома полная проводимость параллельных ветвей Y=I/U_К, а полная проводимость катушки индуктивности Y_K=I_K/U_k.

С оотношение активной G, реактивной В=-(В_L-B_C) и полной Y проводимостей определяется треугольником проводимостей цепи с параллельно включёнными ветвями (рис.2а), откуда следует:

А налогично из треугольника проводимостей для катушки (рис. 2б )

Рисунок 2. а),б),в)-Треугольники соответственно проводимостей всей цепи, катушки и мощностей соответственно; г) векторная диаграмма напряжений и токов участка цепи с параллельно включёнными катушкой и конденсатором.

В соответствии с первым законом Кирхгофа:

I = I_K + I_C = I_ak + I_pk + I_c

В ектор активной составляющей тока катушки I_ak совпадает по направлению с вектором напряжения U_k. Действующее значение активной составляющей :

В ектор реактивной составляющей тока катушки I_pk отстает от век­тора напряжения U_k на 90°. Действующее значение реактивной составля­ющей :

Вектор тока емкостного элемента I_с опережает вектор напряжения на 90°.

Действующее значение этого тока I_с=В_CU_k.

Д ействующее значение общего тока I в цепи и угол φ сдвига фаз между общим током I и напряжением U_k определяются соотношениями:

Возможны три различных соотношения параметров B_L и В_C .

1. B_L > В_C, тогда I_рк > I_C и вектор тока I отстает от вектора напряжения U на угол φ (рис.2,а).

2. B_L < В_C, тогда I_рк < I_C и вектор тока I опережает вектор напряжения U на угол φ (рис.2,б).

3. B_L = В_C, тогда I_рк = I_C, В =0, Y=G, I=I_ak и вектор I совпадает по направлению с вектором U (рис.2,в).

Рисунок 3 – Векторные диаграммы напряжений и токов участка цепи с параллельно включёнными элементами: а) B_L > В_C; б) B_L < В_C; в) B_L < В_C.

На рисунке 3 принято: начальная фаза напряжения U_k равна нулю,

ψ_i= -φ, так как угол сдвига фаз между напряжением и током φ= ψ_u- ψ_i.

Режим работы параллельной цепи, при кото­ром напряжение и общий ток совпадают по фазе (рис. 3.в), на­зывается резонансом токов. Условием наступления резонанса токов является равенство индуктивной и емкостной проводимостей параллельных ветвей, т.е. В_L= В_C.

В работе резонанс токов получают путем изме­нения частоты сигнала.

В момент резонанса полная проводимость Y прини­мает минимальное значение, равное G, а следовательно, минимальным будет и общий ток:

Реактивная составляющая тока катушки I_рк=I_L и ток конденсатора I_c при резонансе токов имеют одинаковые действующие значения и отли­чаются по фазе на 180°, т.е. на векторной диаграмме векторы I_L и I_C имеют равную длину и противоположно направлены (рис. 2.в).

Полная мощность всей цепи S и полная мощность катушки S_K определяются соответственно выражениями:

При резонансе токов Q_L = Q_C, т.е. Q = 0 и полная мощ­ность цепи равна активной мощности (S_РЕЗ= P_РЕЗ). Единицы измерения: Р – Вт, Q – Вар, S – ВА.