Федеральное государственное образовательное учреждение

среднего профессионального образования

«Московский технический колледж»

Курсовой проект по дисциплине

«Математические методы»

Тема: «Применение математических методов при решении логистических задач в розничной торговле рыбой»

Выполнил

студент группы П-418

Грибанов Роман Валерьевич

Руководитель проекта преподаватель спецдисциплин

Кулаков В.С.

Москва

2012

Оглавление

Введение 3

1. Теоретические основы. Транспортная задача. 4

2. Практическая задача 7

2.1 Постановка задачи 7

2.2 Решение задачи 8

3. Разработка программного обеспечения 13

3.1 Входные данные 13

3.2 Описание выходных данных 13

3.3 Основные функции программного обеспечения 14

4 Проведения исследования. 15

Теперь решим ту же задачу с помощью написанного программного обеспечения и сравним полученный результат с результатом полученным ранее: 16

1) Открываем нашу программу: 16

16

2)Нажимаем кнопку «Задать размер» и вводим количество складов и магазинов. Нажимаем «Ок»: 17

17

3)Вводим данные нашей задачи и нажимам кнопку «Рассчитать»: 17

18

4)В memo1 выводятся все итерации и решение: 18

19

Сравнивая полученные результаты программы, выясняем, что «Оптимальный план перевозок», «Распределение товара» и «Транспортный расход» совпадают с результатами, полученными нами при самостоятельном решении данной задачи. Отсюда следует, что написанное программное обеспечение успешно справилось с поставленной задачей и является исправным. 19

Заключение 20

Список используемой литературы 21

Введение

Метод потенциалов. Этот первый точный метод решения транспортной задачи предложен в 1949 году Канторовичем А. В. И Гавуриным М. К. по существу он является детализацией метода последовательного улучшения плана применительно к транспортной задаче. Однако в начале он был изложен вне связи с общими методами линейного программирования. Несколько позднее аналогичный алгоритм был разработан Данциом, который исходил из общей идеи линейного программирования. В американской литературе принято называть модифицированным распределительным методом. Метод потенциалов позволяет определить отправляясь от некоторого опорного плана перевозок построить решение транспортной задачи за конечное число шагов (итераций).

1. Теоретические основы. Транспортная задача.

1.1 Метод потенциалов.

1.2 Постановка транспортной задачи.

В каждом из пунктов P_i, i=1...,m, производится a_i единиц некоторого однородного продукта, а в каждом из пунктов Q_j, j=1...,n, потребляется b_j единиц того же продукта. Возможная транспортировка продукта из каждого пункта производства _Pi в каждый пункт потребления _Qj. Стоимость перевозки единицы продукта из пункта _Pi в пункт _Qj известна и составляет _сіj единиц. Считая, что суммарный объем производства равняется суммарному объему потребления, нужно составить план перевозок продукта, что минимизирует суммарные транспортные расходы.

Математическая модель транспортной задачи имеет вид:

L(x)= c₁₁ x₁₁ +...+ c_1n x_1n +...+ c_m1 x_m1 +...+ c_mn x_mn  min

x_i1 +...+ x_in = a_i, i=1...,m

x_1j +...+ x_mj = b_j, j=1...,n

x_ij0, i=1...,m, j=1...,n

a₁ +...+ a_m = b₁ +...+ b_n.

Последнее условие определяет сбалансированную транспортную задачу.

В предложенной модели назовем вектор x=(x₁₁...,x_1n,...,x_m1,...,x_mn) вектором перевозок, вектор b=(a₁...,a_m,b₁,...,b_n) т — вектором запасов-потребностей, вектор A_ij=(0...,0,1,0...,0,0,...,0,1,0,...,0) ^т — вектором коммуникации PiQj (вектор A_ij имеет размерность m+n, причем первая единица стоит на і-у месте, а вторая — на m+j-у) и, наконец, вектор c=(c₁₁...,c_1n,...,c_m1,...,c_mn) - вектором транспортных расходов.

1.3 Основные определения.

Поскольку транспортная задача является случаем части задачи линейного программирования, для нее имеют силу все общие определения последней. В частности, замеченное относится также и к допустимому базисному решению (ДБР), как невырожденному, так и вырожденному.

Последовательность коммуникаций, среди которых нет одинаковых, вида:

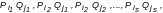
называется маршрутом, что связывает пункты и .

Маршрут, к которому прибавленная коммуникация , называется замкнутым маршрутом (циклом).

Коммуникация PiQj называется основной коммуникацией решения x, если соответствующая ей компонента развязку x_ij>0.

Подобные определения имеют место и для клеточек транспортной таблицы.

1.4 Свойства транспортной задачи.

1. Сбалансированная транспортная задача всегда допустимая и имеет оптимальное решение.

2. Ранг матрицы А ограничений транспортной задачи равняется m+n–1, в результате чего допустимое базисное решение задачи содержит не более m+n–1 ненулевых перевозок x_ij.

3. Если в транспортной задаче все числа a_i, i=1...,m, b_j, j=1...,n — цели, то хотя бы одно оптимальное решение задачи — целочисленный.

1.5 Основные теоремы.

1. Решение транспортной задачи базисное, если из его основных коммуникаций невозможно составить замкнутый маршрут (цикл).

2. ДБР x=(x_ij, i=1...,m, j=1...,n) оптимальный тогда и только затем, когда существуют потенциалы u_i, v_j такие, что

v_j – u_i = с_іj, если x_ij  базисная перевозка

v_j – u_i  с_іj, если x_ij  небазисная перевозка.

1.6 Методы поиска выходного ДБР.

1.6.1 Метод северо-западного угла.

Метод состоит из однотипных шагов, поэтому его формальное изложение дадим лишь для 1-го шага. Заполняем северо-западную клеточку таблицы, покладая x₁₁ = min{a₁, b₁}. Возможные три случая:

1. a₁<b₁, тогда x₁₁=a₁ и вычеркивается 1-я строка таблицы;

2. a₁>b₁, тогда x₁₁=b₁ и вычеркивается 1-й столбец таблицы;

3. a₁=b₁, тогда x₁₁=a₁=b₁ и вычеркивается как 1-я строка, так и 1-й столбец. В последнем случае в одну из вычеркнутых клеточек заносится нулевая базисная перевозка (соответствующий выходной допустимое базисное решение будет вырожденным).

Во всех случаях после заполнения базисной клеточки объемы запасов a₁ и потребностей b₁ уменьшают на величину, что равняется x₁₁. Конец шага.

На каждом из следующих шагов рассматривается «обрезанная» транспортная таблица, то есть вычеркнутые строки и столбцы игнорируются.