Министерство образования и науки Российской Федерации

Озерский технологический институт

(филиал)

Московского инженерно- физического института

( государственного университета)

Лабораторная работа №16

Измерение угла Брюстера

По курсу

Физика (Оптика)

Преподаватель					Карпов В. И.
Выполнил студент группы	1ТМ-20ДС 1МХ-39				Куликов Н. В. Клюшин В. А.
	индекс группы		(дата, подпись)		(Ф.И.О.)

г. Озёрск

2011

Цель работы:	Изучение явления поляризации света при отражении от диэлектрика и определение угла Брюстера.
Приборы и принадлежности:	а) прибор Нёренберга, б) осветитель с понижающим трансформатором.

Введение

Волну, в которой направление колеба­ний светового вектора Е упорядочено каким-либо образом, на­зывают поляризованной. Если колебания вектора Е происходят только в одной плоскости, проходящей через луч, то мы имеем дело с плоско (или линейно) поляризованной волной. Плос­кость, в которой колеблется вектор Е, называют плоскостью поляризации (плоскостью колебаний светового вектора)¹.

Другой вид поляризации заключается в том, что вектор Е вращается вокруг направления распространения волны, одно­временно изменяясь периодически по модулю. При этом конец вектора Е описывает эллипс (в каждой точке среды). Такую волну называют эллиптически-поляризованной. Или поляризованной по кругу, если конец вектора Е описывает окружность.

В зависимости от направления вращения вектора Е различают правую и левую эллиптические (или круговые) поляризации. Если смотреть навстречу распространения волны, и вектор Е при этом поворачивается по часовой стрелке, то поляризацию назы­вают правой, в противном случае (если против часовой стрел­ки) — левой. Волну с эллиптической поляризацией всегда можно разло­жить (или представить) на две взаимно перпендикулярные ли­нейно поляризованные волны с взаимно ортогональными плоско­стями поляризации. Причем разность фаз этих двух волн сохра­няется постоянной во времени. Такие волны, как мы знаем, называют когерентными, в отличие от не когерентных, у которых разность фаз хаотически меняется во времени.

В естественном свете колебания век­тора Е в любой (фиксированной) точке среды совершаются в разных направлениях, быстро и беспорядочно сменяя друг дру­га.

Естественный свет можно представить как суперпозицию (сум­му) двух некогерентных плоско поляризованных волн с взаимно ортогональными плоскостями поляризации. Важно подчеркнуть, что разность фаз этих волн есть случайная функция, изменяющаяся в интервале (‑,+).

Помимо линейно поляризованного и ес­тественного света существует еще промежуточный случай — частично поляризованный свет. Частично поляризованный свет, как и естественный, можно представить в виде суперпозиции естественной и линейно поляризованной составляющих. Интенсивность такого света равна сумме интенсивностей его естественной и поляризованной составляющих.

Частично поляризованный свет характеризуют степенью поляризации Р, которую определяют как

(1).

Здесь I_поляр– интенсивность поляризованной составляющей, I₀ – полная интенсивность частично поляризованного света:

I₀= I_поляр+ I_ест.

Из естественного света можно получить линейно поляризованный с помощью приборов, называемых поляризаторами. Эти приборы свободно пропускают колебания светового вектора, параллельные плоскости, которую называют плоскостью пропускания поляризатора. Колебания же, пер­пендикулярные к этой плоскости, задерживаются.

Поляризаторы можно использовать и в каче­стве анализаторов — для определения характера и степени по­ляризации интересующего нас света. Пусть на анализатор падает линейно поляризованный свет, вектор Е₀ которого составляет угол  с плоскостью пропускания Р. Анализатор пропускает только ту составля­ющую вектора Е₀, которая параллельна плоскости пропускания Р, т. е. Е=Е₀ cos . Интенсивность пропорциональна квадрату модуля светового вектора (I~Е²), поэтому интенсивность пр ошедшего света

I=I₀соs² (2),

где I₀ — интенсивность падающего линейно поляризованного све­та. Это соотношение и выражает собой закон Малюса. Если на поляризатор падает неполяризованный свет, то независимо от направления плоскости пропускания анализатора интенсивность прошедшего через него света будет одной и той же. С помощью закона Малюса можно показать, что через поляризатор пройдет ровно половина падающего на него естественного света.

При падении естественного света на границу двух диэлектриков, отраженный и преломленный лучи частично поляризуются.

При угле падения _бр, удовлетворяющем условию:

(3),

г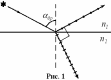 де n₁ и n₂ – показатели преломления первой и, соответственно, второй среды, отраженный луч оказывается линейно поляризованным. Плоскость колебаний в отраженном луче (плоскость вектора Е) перпендикулярна плоскости падения. Преломленный луч поляризован частично и преимущественное направление плоскости колебаний в этом луче совпадает с плоскостью падения (Рис. 1).

Соотношение (3) носит название закона Брюстера, угол падения _бр – называется углом Брюстера или углом полной поляризации. Легко показать, что если угол падения равен углу Брюстера, то угол между отраженным и преломленным лучами равен /2.

Если угол падения не равен углу Брюстера, то и отраженный и преломленный лучи оказываются частично поляризованными. Степень поляризации можно определить из формул Френеля, связывающих амплитуды падающего, отраженного и преломленного света. Эти формулы, в свою очередь, являются следствиями граничных условий для электрического и магнитного поля на границе раздела двух сред:

Е₀ – амплиту да напряженности электрического поля в падающей волне, Е₁ – в отраженной, Е₂ – в преломленной. Эти соотношения име­ют место, если падающий свет поляризован перпендикулярно плоскости падения.

Для случая, когда направление поляризации падающего света параллельно плоскости падения, справедливы формулы (5), где Н с соответствующим индексом – амплитуда напряженности магнитного поля в той или иной волне.

Нетрудно видеть, что из (5) следует закон Брюстера. Действительно, если отраженной волны нет, то Н₁=0. Это равенство имеет место, если в первой из формул (5) числитель обращается в нуль: . Возводя это равенство в квадрат, и используя известную формулу , получим tg=n₂/n₁.

При пользовании формулами Френеля (4) и (5) следует иметь в виду, что интенсивность световой волны пропорциональна квадрату амплитуды волны, а коэффициент отражения света R равен отношению потоков энергии в отраженной и падающей волнах в направлении, перпендикулярном границе раздела диэлектриков. Поскольку угол отражения равен углу падения, то R равен просто отношению интенсивностей отраженной и падающей волн:

R=I₁/I₀.

Для определения интенсивности преломленной волны следует учесть, что в направлении, перпендикулярном границе раздела диэлектриков, поток энергии в падающей волне перераспределяется между отраженной и преломленной волнами:

I₀cos₀=I₁ cos₀+I₂ cos₂.

Здесь ₀ – угол падения, ₂ – угол преломления.