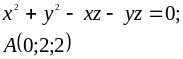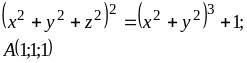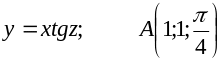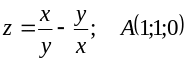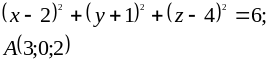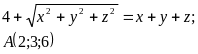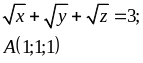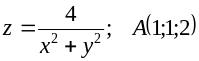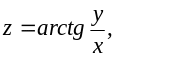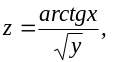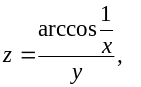Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Украинский Государственный химико-технологический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Метод.rtf

Скачиваний:

Добавлен:

16.07.2019

Размер:

14.13 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

11. Найбільше та найменше значення функції в замкненій області

Функція, неперервна в замкненій області D, обов’язково має найбільше і найменше значення в цій області.

Найбільше і найменше значення неперервної в замкненій області функції досягають у внутрішніх точках області (або на межі області), збігаючись відповідно з максимальним або мінімальним значеннями функції.

Тому для пошуку найбільшого і найменшого значень функції в певній замкненій області треба знайти всі внутрішні критичні точки, обчислити в них значення функції, порівняти їх з найбільшим і найменшим значеннями функції на межі області. Найбільше і найменше з цих значень будуть найбільшим та найменшим значеннями неперервної функції в даній замкненій області.

Приклад 20. Знайти найбільше та найменше значення функції в області, обмеженій лініями .

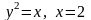Розв'язок:

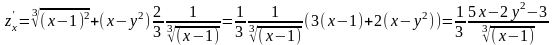
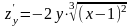Для знаходження стаціонарних точок прирівняємо до нуля частинні похідні даної функції. Одержимо систему рівнянь

Звідси маємо х=3/5,' у=0, стаціонарна точка належить заданій області значення функції у ній дорівнює .

Критичними точками для заданої функції є і точки хорди 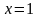, бо в цих точках . У всіх точках цієї хорди .

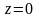Дослідимо функцію на межі області, яка складається з частини параболи і хорди тієї ж параболи.

На параболі, рівняння якої , функція має вигляд 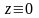, тобто на цій частині межі області задана функція дорівнює нулю .

На хорді, рівняння якої 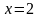, функція має вигляд . Значення цієї функції в стаціонарній точці у=^;0 і в граничних точках 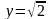, відповідно дорівнюють 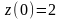, , . Порівнюючи всі знайдені значення функції визначимо, що задана функція має найбільше значення (досягається в точці (2;0)) і найменше значення (досягається на хорді х=1 і на частині параболи ).

12. Індивідуальні завдання

Завдання 1

Знайти та побудувати область визначення функції

1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

Завдання 2

Знайти частинні похідні та функцій:

1.	а)
	б)
	в)
2.	а)
	б)
	в)
3.	а)
	б)
	в)
4.	а)
	б)
	в)
5.	а)
	б)
	в)
6.	а)
	б)
	в)
7.	а)
	б)
	в)
8.	а)
	б)
	в)

9.	а)
	б)
	в)
10.	а)
	б)
	в)
11.	а)
	б)
	в)
12.	а)
	б)
	в)
13.	а)
	б)
	в)
14.	а)
	б)
	в)
15.	а)
	б)
	в)
16.	а)
	б)
	в)

17.	а)
	б)
	в)
18.	а)
	б)
	в)
19.	а)
	б)
	в)
20.	а)
	б)
	в)
21.	а)
	б)
	в)
22.	а)
	б)
	в)
23.	а)
	б)
	в)
24.	а)
	б)
	в)

25.	а)
	б)
	в)
26.	а)
	б)
	в)
27.	а)
	б)
	в)
28.	а)
	б)
	в)
29.	а)
	б)
	в)
30.	а)
	б)
	в)

Завдання 3

З’ясувати, чи задовольняє функція z = f (x; y) даному рівнянню.

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.

Завдання 4

Знайти перші похідні та повний диференціал функції

1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

Завдання 5

Обчислити наближено значення функції z=f(x;y) у заданій точці (x₁;y₁), якщо використати значення функції у точці (x₀;y₀).

№ п/п	z=f(x;y)	(x₁;y₁)	(x₀;y₀)
1		(0.02;2.03)	(0;2)
2		(1.04;1.99)	(1;2)
3		(1.55;0.015)	( )
4		(0.97;1.05)	(1;1)
5		(0.95;1.02)	(1;1)
6		(4.05;3.07)	(4;3)
7		(0.09;0.99)	(0;1)
8		(1.02;0.05)	(1;0)
9		(1.02;1.97)	(1;2)
10		(1.04;.2.03)	(1;2)
11		(1.05;0.98)	(1;1)
12		(1.02;0.93)	(1;1)
13		(4.01;2.99)	(4;3)
14		(1.98;3.97)	(2;4)
15		(0.99;1.01)	(1;1)
16		(1.03;2.98)	(1;3)
17		(5.02;4.96)	(5;5)
18		(4.04;1.03)	(4;1)
19		(2.97;2.02)	(3;2)
20		(2.02;1.04)	(2;1)
21		(1.97;3.03)	(2;3)
22		(0.96;1.02)	(1;1)
23		(1.02;0.96)	(1.1)
24		(3.03;2.04)	(3;2)
25		(1.98;0.97)	(2;1)
26		(4.02;0.97)	(4;1)
27		(1.1;0.9)	(1;1)
28		(1.05;2.99)	(1;3)
29		(0.04;0.02)	(0;0)
30		(2.99;4.01)	(3;4)

Завдання 6

Знайти частинні похідні функції z, яка задана неявно

1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

Завдання 7

1	Дана функція z=arctg де u = xsiny v=xcosy. Знайти .
2	Знайти і якщо z=arcsin де y=1+x .
3	Знайти та якщо z=f(u,v), де u=ln(x -y ). v=x y .
4	Знайти повну похідну функції z=xsinvcosw, якщо v=ln(x +1), w=1-x .
5	Знайти , якщо u=tg , x=lnt, y=t .
6	Знайти , якщо u= x -y , де x=e , y=sint.
7	Знайти , якщо sinxy-e - x y=0.
8	Знайти та , якщо z=ln , де u=x, v= x -y .
9	Знайти , якщо z=arctg , де x=e +1, y= e -1.
10	Знайти і , якщо z=arctg , де y=e .
11	Знайти та , якщо z=ln , де u=a+by, v=ax-by.
12	Знайти dz, якщо z=f(u,v), де u=sin , v= .
13	Знайти та , якщо z=f(u,v), де u=ln(x -y ), v=xy .
14	Знайти , , якщо z=arctg , де u=xsiny, v=xcosy.
15	Знайти , якщо u= , де x=2cost, z=2, y=2sint.
16	Знайти , якщо u=tg(3x+2y -z), де y= , z=x.
17	Знайти і ,якщо z=arcsin ,де y=1- x .
18	Знайти та , якщо z=f(u,v), де u=ln(x +y ), v=x y .
19	Знайти і , якщо z= u ln , де u=sin xy, v=sin(xy) .
20	Знайти якщо z=arcsin , де y= x +x.
21	Знайти повну похідну функції z=xsinvcosw, якщо v=ln(x +1), w=-sin x +1-x.
22	Знайти , якщо u=cos , x= lnsint, y=t .
23	Знайти , якщо u= arctg(xy), y=sinx.
24	Знайти , якщо u= x +4xy+ y ,де x=e ,y=sint.
25	Знайти , , якщо z= ln , де u=tgx, v= x + y .
26	Знайти dz ,якщо z=f(u,v), де u=sin , v= cos .
27	Знайти та , якщо z=f(u,v), де u=ln(x + sin y ), v= x y .
28	Знайти dz якщо x=u+v, y= u +v ,z=u +v .
29	Знайти , якщо z= cos(sin ), x= sint, y=(t +1) .
30	Знайти та , якщо z=ctg , де u=xsiny, v=xcosy.
31	Знайти , якщо u= де x=2cost, z=2t.

Завдання 8

Знайти другі похідні:

1.	а) ;	б) ;
2.	а) ;	б) ;
3.	а) ;	б) ;
4.	а) ;	б) ;
5.	а) ;	б) ;
6.	а) ;	б) ;
7.	а) ;	б) ;
8.	а) ;	б) ;
9.	а) ;	б) ;
10.	а) ;	б) ;
11.	а) ;	б) ;
12.	а) ;	б) ;
13.	а) ;	б) ;
14.	а) ;	б) ;
15.	а) ;	б) ;
16.	а) ;	б) ;
17.	а) ;	б) ;
18.	а) ;	б) ;
19.	а) ;	б) ;
20.	а) ;	б) ;
21.	а) ;	б) ;
22.	а) ;	б) ;
23.	а) ;	б) ;
24.	а) ;	б) ;
25.	а) ;	б) ;
26.	а) ;	б) ;
27.	а) ;	б) ;
28.	а) ;	б) ;
29.	а) ;	б) ;
30.	а) ;	б) .

Завдання 9

Для даної поверхні F(x, y, z)=0 записати рівняння дотичної площини і нормалі у точці А.

1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

Завдання 10

Знайти

а) градієнт функції 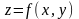у точці А;

б) похідну функції у точці А за напрямком вектора .

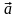1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.

Завдання 11

Знайти екстремуми функції

а)

б)

а)

б)

а)

б)

а)

б)

а)

б)

а)

б)

а)

б)

а)

б)

а)

б)

10.

а)

б)

11.

а)

б)

12.

а)

б)

13.

а)

б)

14.

а)

б)

15.

а)

б)

16.

а)

б)

17.

а)

б)

18.

а)

б)

19.

а)

б)

20.

а)

б)

21.

а)

б)

22.

а)

б)

23.

а)

б)

24.

а)

б)

25.

а)

б)

26.

а)

б)

27.

а)

б)

28.

а)

б)

29.

а)

б)

30.

а)

б)

Завдання 12

Знайти найбільше значення функції
1.		у замкнутому трикутнику, обмеженому осями координат і прямою
2.		в замкнутому трикутнику, обмеженому прямими
3.		в квадраті, обмеженому осями координат і прямими
4.		у замкнутому трикутнику, обмеженому осями координат і прямою
5.		в прямокутнику з вершинами , , ,
6.		в прямокутнику D
7.		в замкнутому трикутнику, обмеженому осями координат і прямою
8.		в замкнутому трикутнику, обмеженому прямою та осями координат
9.		в колі
10.		в колі
11.		в замкнутій області, обмеженій еліпсом
12.		в замкнутій області, обмеженій параболою та прямою
13.		в замкнутій області, обмеженій параболою та прямою
14.		в замкнутій області, обмеженій еліпсом
15.		в замкнутій області, обмеженій гіперболою та прямою
Знайти найменше значення функції:
16.		у замкнутому трикутнику, обмеженому осями координат і прямою
17.		в замкнутому трикутнику, обмеженому прямими
18.		в квадраті, обмеженому осями координат і прямими
19.		у замкнутому трикутнику, обмеженому осями координат і прямою
20.		в прямокутнику з вершинами , , ,
21.		в прямокутнику D
22.		в замкнутому трикутнику, обмеженому осями координат і прямою
23.		в замкнутому трикутнику, обмеженому прямою та осями координат
24.		в колі
25.		в колі
26.		в замкнутій області, обмеженій еліпсом
27.		в замкнутій області, обмеженій параболою та прямою
28.		в замкнутій області, обмеженій параболою та прямою
29.		в замкнутій області, обмеженій еліпсом
30.		в замкнутій області, обмеженій гіперболою та прямою

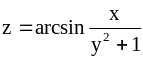
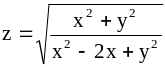
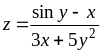
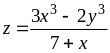
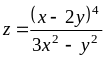
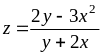
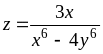
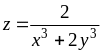
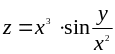
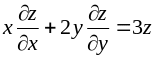
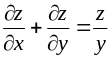
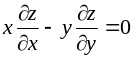
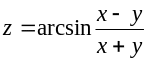
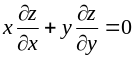
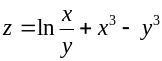
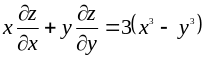
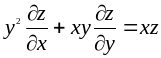
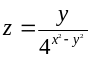
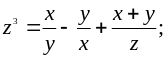
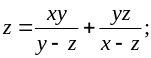
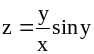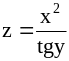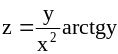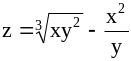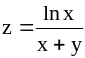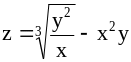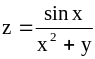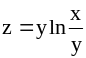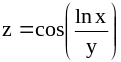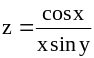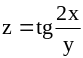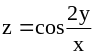<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.11.2019743.42 Кб6Метод. Лаб. ТОТ 2010.doc
#
09.08.20191.26 Mб3Метод. Лаб.роб. ТОТ.doc
#
31.08.2019369.15 Кб3Метод. оф диплом. 2012.doc
#
09.11.2019989.7 Кб3Метод. по М.Э..doc
#
01.05.2025351.74 Кб0Метод. УДХТУ диплом. 2014.doc
#
16.07.201914.13 Mб36Метод.rtf
#
01.05.20251.04 Mб0Метод.вказ.Страхування.doc
#
11.09.201995.23 Кб1Метод.указ. по практике 3 курс КИБ.doc
#
20.02.20161.11 Mб10метод1.doc
#
14.11.2019303.1 Кб4метод10-й тетр_2.doc
#
20.02.2016242.18 Кб6метод1370 фин мен..doc

1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

1.	а)
	б)
	в)
2.	а)
	б)
	в)
3.	а)
	б)
	в)
4.	а)
	б)
	в)
5.	а)
	б)
	в)
6.	а)
	б)
	в)
7.	а)
	б)
	в)
8.	а)
	б)
	в)

9.	а)
	б)
	в)
10.	а)
	б)
	в)
11.	а)
	б)
	в)
12.	а)
	б)
	в)
13.	а)
	б)
	в)
14.	а)
	б)
	в)
15.	а)
	б)
	в)
16.	а)
	б)
	в)

17.	а)
	б)
	в)
18.	а)
	б)
	в)
19.	а)
	б)
	в)
20.	а)
	б)
	в)
21.	а)
	б)
	в)
22.	а)
	б)
	в)
23.	а)
	б)
	в)
24.	а)
	б)
	в)

25.	а)
	б)
	в)
26.	а)
	б)
	в)
27.	а)
	б)
	в)
28.	а)
	б)
	в)
29.	а)
	б)
	в)
30.	а)
	б)
	в)

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.

1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.

1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

1.	а)
	б)
	в)
2.	а)
	б)
	в)
3.	а)
	б)
	в)
4.	а)
	б)
	в)
5.	а)
	б)
	в)
6.	а)
	б)
	в)
7.	а)
	б)
	в)
8.	а)
	б)
	в)

9.	а)
	б)
	в)
10.	а)
	б)
	в)
11.	а)
	б)
	в)
12.	а)
	б)
	в)
13.	а)
	б)
	в)
14.	а)
	б)
	в)
15.	а)
	б)
	в)
16.	а)
	б)
	в)

17.	а)
	б)
	в)
18.	а)
	б)
	в)
19.	а)
	б)
	в)
20.	а)
	б)
	в)
21.	а)
	б)
	в)
22.	а)
	б)
	в)
23.	а)
	б)
	в)
24.	а)
	б)
	в)

25.	а)
	б)
	в)
26.	а)
	б)
	в)
27.	а)
	б)
	в)
28.	а)
	б)
	в)
29.	а)
	б)
	в)
30.	а)
	б)
	в)

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.

1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.

1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

1.	а)
	б)
	в)
2.	а)
	б)
	в)
3.	а)
	б)
	в)
4.	а)
	б)
	в)
5.	а)
	б)
	в)
6.	а)
	б)
	в)
7.	а)
	б)
	в)
8.	а)
	б)
	в)

9.	а)
	б)
	в)
10.	а)
	б)
	в)
11.	а)
	б)
	в)
12.	а)
	б)
	в)
13.	а)
	б)
	в)
14.	а)
	б)
	в)
15.	а)
	б)
	в)
16.	а)
	б)
	в)

17.	а)
	б)
	в)
18.	а)
	б)
	в)
19.	а)
	б)
	в)
20.	а)
	б)
	в)
21.	а)
	б)
	в)
22.	а)
	б)
	в)
23.	а)
	б)
	в)
24.	а)
	б)
	в)

25.	а)
	б)
	в)
26.	а)
	б)
	в)
27.	а)
	б)
	в)
28.	а)
	б)
	в)
29.	а)
	б)
	в)
30.	а)
	б)
	в)

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.

1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.