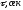Otchet_khtp_4
.docxРоссийский химико-технологический университет им. Д.И.Менделеева
Кафедра информатики и компьютерного моделирования
Лабораторная работа № 4
по курсу
«Компьютерное моделирование химических процессов»
Обработка данных активного эксперимента.
Вариант №1
Сдала:
Приняла: Царева Е.В.
Москва 2019
Результаты эксперимента:
|
№ |
T,K |
|
СА |
||
|
1 |
320 |
50 |
0,0767 |
||
|
2 |
340 |
50 |
0,0343 |
||
|
3 |
320 |
100 |
0,0439 |
||
|
4 |
340 |
100 |
0,0212 |
||
|
5 |
316.8 |
75 |
0,0702 |
||
|
6 |
343.2 |
75 |
0,0249 |
||
|
7 |
330 |
42 |
0,0509 |
||
|
8 |
330 |
108 |
0,0252 |
||
|
9 |
330 |
75 |
0,0304 |
||
|
10 |
330 |
75 |
0,0325 |
||
|
11 |
330 |
75 |
0,0328 |
||
|
12 |
330 |
75 |
0,0336 |
||
|
13 |
330 |
75 |
0,033 |
||
|
14 |
330 |
75 |
0,0336 |
||
Найдем коэффициенты линейного уравнения
регрессии для компонента P
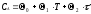на основе данных полного факторного
эксперимента.
Центр планирования: Т0 =330 К –
температура проведения реакции и
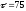сек
– время проведения реакции. Интервалы
изменения параметров соответственно
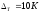и
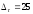сек
Для построения уравнения регрессии
запишем нашу зависимость в кодированных
переменных
,
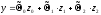где
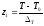и
,
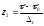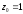- фиктивный фактор
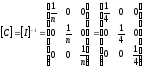
Тогда решим следующую систему (записана в матричном ви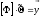де):
где:
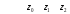
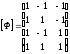- матрица планирования;
;
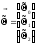
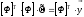
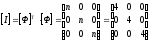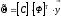
- информационная матрица
- корреляционная матрица
Решая
данную систему уравнений в матричном
виде получим:
=
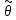Наша зависимость записанная в кодированных переменных:
y=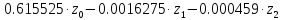
Искомое
уравнение регрессии:
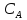=0,6706095-0.016275
T-0,00001836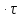
Среднее арифметическое измерений во всех параллельных опытах: yср=0.03265
Проверим значимость коэффициентов уравнения регрессии:
=
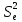=1.407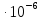
=
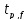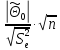= 74.2305>
(p=0,95,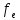
=5)
= 2,57– коэффициент значимый
=
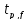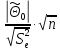= 27.4413>
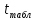(p=0,95,
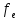=5)
= 2,57– коэффициент значимый
=
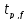= 19.348>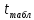
(p=0,95,
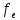=5)
= 2,57– коэффициент значимый
Проверим данное уравнение регрессии на адекватность с помощью критерия Фишера:
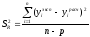=0.000097
(n=4; p=3)
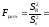68,94>FT=6,61
– уравнение регрессии неадекватно
Найдем коэффициенты нелинейного
уравнения регрессии для компонента А
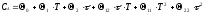на основе данных полного факторного
эксперимента.
Центр планирования: Т0 =330 К –
температура проведения реакции и
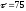сек
– время проведения реакции. Интервалы
изменения параметров соответственно
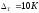и
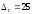сек
Для построения уравнения регрессии
запишем нашу зависимость в кодированных
переменных
,
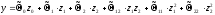где
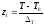и
,
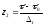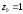- фиктивный фактор
Тогда решим следующую систему (записана в матричном ви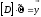де):
где:
a=1,32
s=0,534
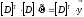
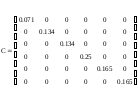
Матрица планирования:
z0 z1
z2
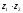
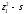
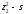
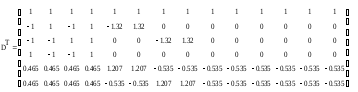
Информационная
матрица:
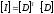
Корреляционная
матрица:
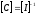
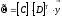
Тогда уравнение в кодированных переменных примет вид:
y=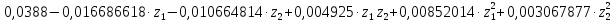
Искомое уравнение регрессии:
+
+
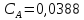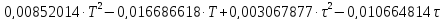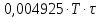
Проверим значимость коэффициентов уравнения регрессии:
=
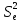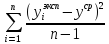=1.407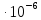
=
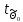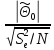= 122,3907778>
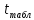(p=0,95,
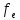=5)
= 2,57– коэффициент значимый
=
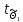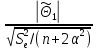= 38,48676259>
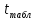(p=0,95,
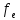=5)
= 2,57– коэффициент значимый
=
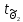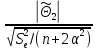= 24,59780407>
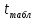(p=0,95,
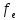=5)
= 2,57– коэффициент значимый
=
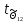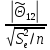= 8,304035206>
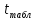(p=0,95,
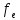=5)
= 2,57– коэффициент значимый
=
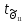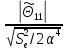= 17,69954099>
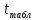(p=0,95,
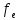=5)
= 2,57– коэффициент значимый
=
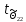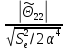= 6,373135396>
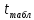(p=0,95,
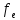=5)
= 2,57– коэффициент значимый
Проверим данное уравнение регрессии на адекватность с помощью критерия Фишера:
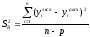=3,36047
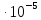(n=14;
p=6)
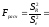2.3884
< FT=3.3258
– зависимость адекватна
Найдем координаты экстремальной точки функции СА
+
+
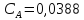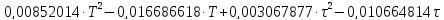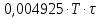
Для
этого найдем частные производные по T
,
и решим СЛАУ
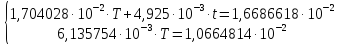
Решая систему, получаем:
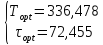
Выводы.
Проведена обработка данных активного эксперимента по определению зависимости концентрации компонента Р от времени и температуры. Обработка данных производилась следующим образом:
-
Определялись коэффициенты уравнения регрессии – линейного и нелинейного.
-
Оределялась значимость коэффициентов уравнений регрессии с помощью расчетного коэффициента Стьюдента
-
Определялась адекватность уравнений регрессии с использованием распределения Фишера из условия
-
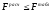
Полученные уравнения в кодированных переменных преобразованы в нормальный вид.
Линейная:
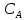=0.044025-0.016275
T-0.011475
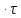- зависимость не адекватна т.к.
Fрасч=68,94>FT=6,61
Нелинейная:
+
+
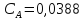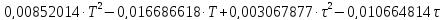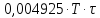
- зависимость адекватна т.к. Fрасч=2.3884 < FT=3.3258