
ГОУ ВПО «АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Математический факультет
Кафедра теоретической кибернетики и прикладной математики
Модель планирования объединения производственных предприятий
Методические указания к лабораторным работам по курсу
«Исследование систем управления»
БАРНАУЛ – 2011
Модель планирования объединения предприятий
Рассмотрим
следующую экономическую ситуацию.
Объединение состоит из T
предприятий, каждое из которых выпускает
продукцию
![]() видов, потребляя ресурсы объединения
и ресурсы, являющиеся «собственностью»
предприятий.
видов, потребляя ресурсы объединения
и ресурсы, являющиеся «собственностью»
предприятий.
Предполагаются
известными матрицы
![]() норм потребления ресурсов, векторы
норм потребления ресурсов, векторы
![]() лимитов ресурсов соответственно
объединения и локальных ресурсов
предприятий и вектор
лимитов ресурсов соответственно
объединения и локальных ресурсов
предприятий и вектор
![]() коэффициентов дохода от реализации
продукции предприятием
коэффициентов дохода от реализации
продукции предприятием
![]() .
Требуется найти сбалансированный по
ресурсам план выпуска продукции, дающий
максимальный доход объединению.
.
Требуется найти сбалансированный по
ресурсам план выпуска продукции, дающий
максимальный доход объединению.
Общая система условий модели планирования объединения имеет блочно-диагональную структуру следующего вида:
![]() ; (1)
; (1)
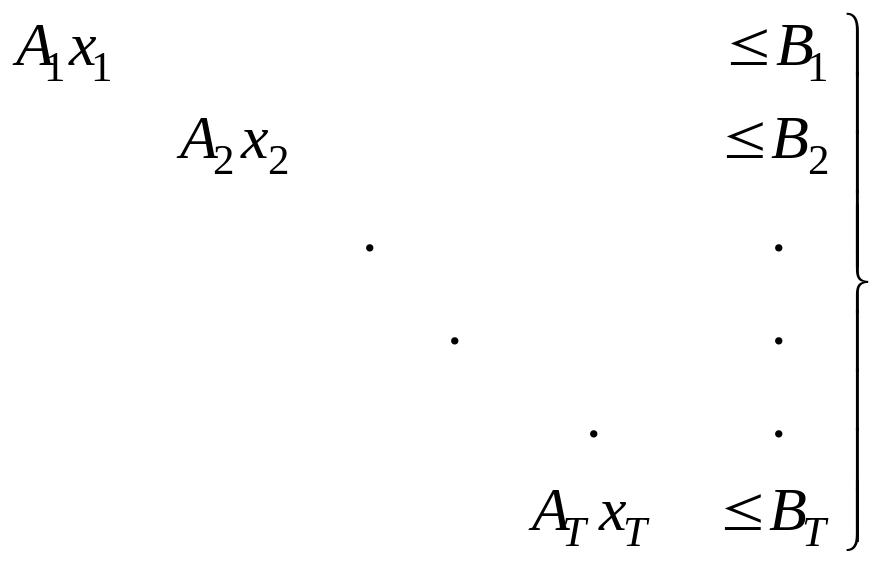 ; (2)
; (2)
![]() ; (3)
; (3)
![]() . (4)
. (4)
Симплекс-метод будем применять к задаче (1)–(4), переписав ее условия в следующем виде:
![]() , (5)
, (5)
где
![]() – число блоков (бизнес-единиц);
– число блоков (бизнес-единиц);
![]() – допустимое множество планов блока
– допустимое множество планов блока
![]() :
:
![]() .
.
Матрицы в приведенных выражениях имеют следующие размерности:
![]()
![]() ,
где первое число показывает число строк,
второе – число столбцов.
,
где первое число показывает число строк,
второе – число столбцов.
Решение задачи линейного программирования находим в среде MS Excel с использованием инструмента «Поиск решения». Индивидуальное задание предусматривает генерирование условий задачи планирования для своих исходных данных и ее решение. Порядок генерации числовых данных приведен в программе *.xls, которая прилагается.
Задания для лабораторной работы «Исследование задачи планирования объединения предприятий»
Цель работы и задания приведены в конце методических указаний.
Исходные данные для расчетов приведены в таблице 2, список индивидуальных заданий приведен в таблице 3.
Таблица 2
Таблица вариантов индивидуальных заданий для модели планирования объединения
Наим.пар. |
Пр 1 |
Пр 2 |
Пр 3 |
Пр 4 |
Пр 5 |
Пр 6 |
Пр 7 |
Пр 8 |
Пр 9 |
Пр 10 |
Ptниз |
-1 |
-2 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
0 |
Ptверх |
5 |
6 |
7 |
8 |
7 |
6 |
5 |
6 |
7 |
8 |
Nt |
2 |
3 |
4 |
4 |
3 |
2 |
3 |
4 |
4 |
3 |
Mt |
4 |
3 |
5 |
4 |
2 |
4 |
3 |
5 |
4 |
2 |
Atниз |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Atверх |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
0,4 |
Btниз |
40 |
40 |
50 |
80 |
70 |
30 |
60 |
80 |
60 |
50 |
Btверх |
50 |
60 |
100 |
150 |
100 |
50 |
70 |
90 |
80 |
60 |
Actниз |
0,3 |
0,3 |
0,3 |
0,3 |
0,3 |
0,3 |
0,3 |
0,3 |
0,3 |
0,3 |
Actверх |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
1,1 |
1,2 |
1,3 |
Для всех вариантов следует принять m=2, B1=250, B2=200.
Варианты индивидуальных заданий формируются выборкой из таблицы пяти заданных предприятий (Номер индивидуального задания студента совпадает с его номером в лаб-1).
Таблица 3.
