Главные оси и главные моменты инерции
81) Главные центральные
оси инерции проходят через точку…
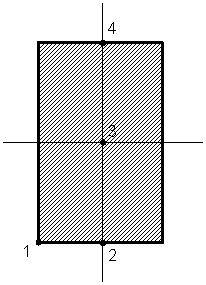
1
2
4
3
82) В формуле для
нормального напряжения при косом изгибе
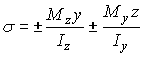величины
и
есть…
статистические моменты относительно главных центральных осей
моменты инерции относительно главных осей
центральные моменты инерции относительно главных осей
моменты инерции относительно главных центральных осей поперечного сечения
83) Оси Y
и Z
– главные центральные оси поперечного
сечения. А – площадь сечения.
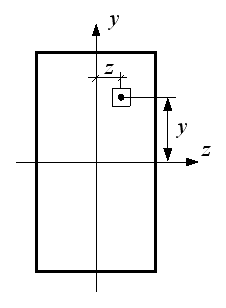В
этом случае…
84)
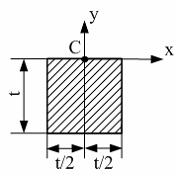Оси
x
и y –
главные оси для точки С. Максимальный
из главных моментов инерции квадрата
равен…
85)
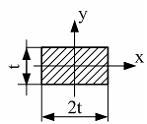Момент
инерции прямоугольника относительно
оси y
равен…
Моменты инерции простых и сложных сечений
86) Полярный момент
инерции кольцевого сечения, внутренний
радиус которого
наружный
–
,
равен …
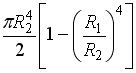
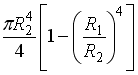
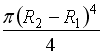
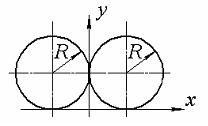
87) Осевой момент
инерции
составного
сечения, показанного на рисунке, равен…
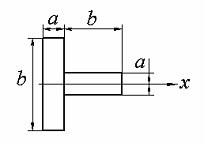
88) Осевой момент
инерции
составного
сечения, показанного на рисунке, равен…
89)
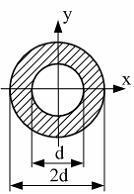Момент
инерции относительно оси x
равен…
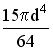
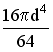
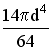
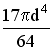
90)
-
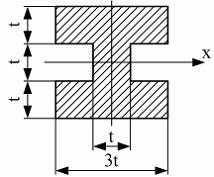
формула параллельного переноса. Момент
инерции относительно оси x
равен…
ДЕ №6 ПЛОСКИЙ ПРЯМОЙ ИЗГИБ
Поперечная сила, изгибающий момент и их эпюры
91)
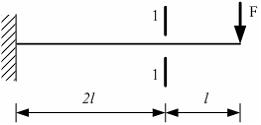Изгибающий
момент
,
действующий в сечении 1-1, равен …
Fl
3Fl
2Fl
0
92) Шарнирно опертая
балка нагружена распределенной нагрузкой
q.
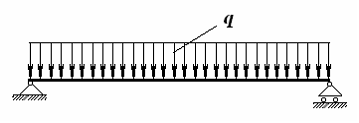Эпюра
изгибающих моментов для этой балки
имеет вид …
(эпюра строится на сжатых
волокнах)
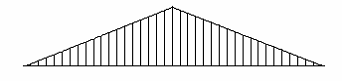
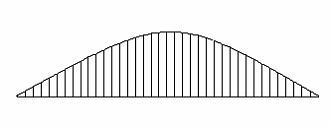
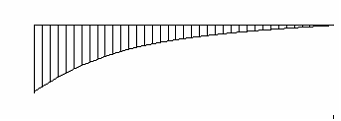
93) Эпюра изгибающих моментов, построенная на сжатых волокнах, для балки имеет вид. Этой эпюре соответствует нагружение балки, представленное на рисунке …
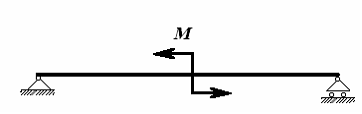
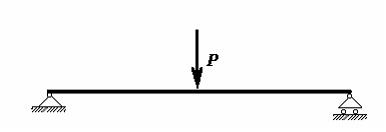
94) В поперечном
сечении балки при изгибе могут возникать
внутренние силовые факторы:
–
поперечная сила и
–
изгибающий момент. В сечении 1-1
балки, представленной на рисунке …
есть и
есть только
нет и
есть только
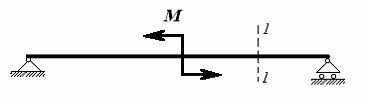
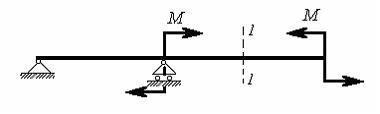
95) В поперечном
сечении балки при изгибе могут возникать
внутренние силовые факторы:
–
поперечная сила и
–
изгибающий момент. В сечении 1-1
балки, представленной на рисунке, …
есть только
нет и
есть только
есть и
Напряжения в поперечном сечении стержня при плоском изгибе (Напряжения в поперечном сечении балки)
96)
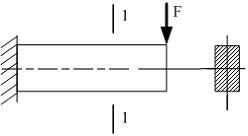Эпюра
касательных напряжений в сечении 1-1
имеет вид …
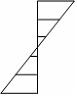
97)
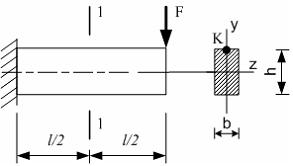Нормальное
напряжение
в
точке K сечения 1-1 равно …
0
98) При нагружении
балки прямоугольного поперечного
сечения высотой
и
шириной
в
сечении возникают изгибающий момент
и
поперечная сила
.
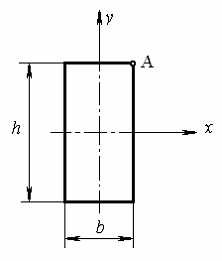Нормальные
и касательные напряжения в точке А
сечения соответственно равны…
;
;
;
;
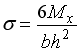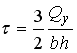
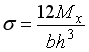99) При нагружении
балки прямоугольного поперечного
сечения высотой
и
шириной
в
сечении возникают изгибающий момент
и
поперечная сила
.
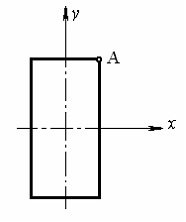Нормальное
и касательное напряжения в точке А
сечения соответственно равны…
;
;
;
;
100) При нагружении
балки таврового сечения с моментом
инерции относительно центральной оси
,
равным
,
в сечении возникает изгибающий момент
.
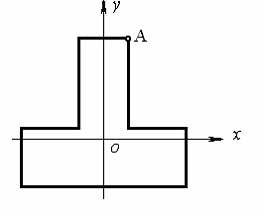Нормальное
и касательное напряжения в точке А
сечения соответственно равны…
;
;
;
;