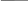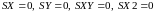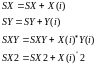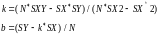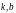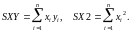4 Пример поиска приближающей функции методом наименьших квадратов

Построим приближающую функцию методом наименьших квадратов для зависимости, заданной таблицей.

x	1,1	1,7	2,4	3,0	3,7	4,5	5,1	5,8
f(x)	0,3	0,6	1,1	1,7	2,3	3,0	3,8	4,6

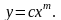Точечный график изображен на рисунке 1.8. Вид приближающей кривой не очевиден, поэтому рассмотрим два способа приближения заданной функции: в виде прямой и в виде степенной функции После нахождения значений параметров и m найдем суммы квадратов уклонений (1.2) и по их значениям установим какое из двух приближений лучше.

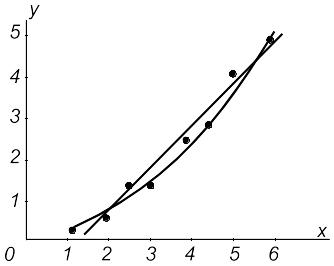
Рис. 1.8

ввод данных да нет печать Рис.1.9

Значения параметров k, b линейной функции находятся из системы вида 1.4. Блок-схема расчета параметров линейной регрессии приведена на рисунке 1.9. В блок-схеме используются следующие обозначения: Замечание: приведенная блок-схема позволяет рассчитать лишь значения параметров линейной регрессии, но не дает величины средней квадратичной ошибки (блок-схему для расчета величины читателю предлагаем составить самостоятельно).

Проделав необходимые вычисления, получаем:

Т.е. приближающее линейное уравнение запишется в виде

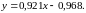
Для нахождения параметров c и m степенной функции воспользуемся формулой (1.7). Составив соответствующую программу для ЭВМ, получим:

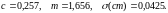
Таким образом, уравнение степенной регрессии имеет вид

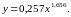
Как видно, сумма квадратов абсолютных погрешностей для линейной функции составляет 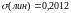, для степенной функции — 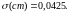Видно, что приближение в виде степенной функции в данном случае предпочтительнее.

Для решения задачи приближения функции методом наименьших квадратов сформулируем основные шаги алгоритма.

1. Ввод исходных данных.

2. Выбор вида уравнения регрессии.

3. Преобразование данных к линейному типу зависимости.

4. Получение параметров уравнения регрессии.

5. Обратное преобразование данных и вычисление суммы квадратов

отклонений вычисленных значений функции от заданных.

6. Вывод результатов.