Термодинамическая система. Микро- и макрохарактеристики системы. Макроскопическое состояние. Макроскопические параметры как средние значения. Температура.
Термодинамическая система, объект изучения термодинамики, совокупность физ. тел, которые могут взаимодействовать энергетически между собой и с другими телами, а также обмениваться с ними веществом. Т. с. состоят из столь большого числа частиц, что их состояние можно характеризовать макроскопическими параметрами: плотностью, давлением, концентрацией разных веществ, образующих её.
Микроскопическое состояние (или микросостояние) — это состояние системы, определяемое заданием координат и импульсов всех составляющих систему частиц.
Макроскопическое состояние (или макросостояние) — это состояние системы, характеризуемое небольшим числом величин (Р, V, T) и, быть может, еще некоторыми другими.
Величины, характеризующие макросостояние, называются макроскопическими характеристиками. Величины, характеризующие микросостояние, называются микроскопическими характеристиками.
Примерами макроскопических характеристик являются: давление, объем, температура и количество вещества.
Примерами микроскопических характериктик являются: количество частиц в веществе, температура одной частицы и т.д.
p
= nkT
Температура - это физическая величина, характеризующая степень нагрева предмета, измеряемую в градусах по шкале Цельсия, Фаренгейта и некоторым другим.
Основное уравнение молекулярно-кинетической теории для идеального газа устанавливает связь легко измеряемого макроскопического параметра — давления — с такими микроскопическими параметрами газа, как средняя кинетическая энергия и концентрация молекул.
Но, измерив только давление газа, мы не можем узнать ни среднее значение кинетической энергии молекул в отдельности, ни их концентрацию. Следовательно, для нахождения микроскопических параметров газа нужны измерения еще какой-то физической величины, связанной со средней кинетической энергией молекул. Такой величиной в физике является температура.
Абсолютная
шкала температур. Шкала
измерения температуры в соответствии
с уравнением
называетсяабсолютной
шкалой. Ее
предложил английский физик У. Кельвин
(Томсон) (1824—1907), поэтому шкалу называют
также шкалой
Кельвина.
До введения абсолютной шкалы температур в практике получила широкое распространение шкала измерения температуры по Цельсию. Поэтому единица температуры по абсолютной шкале, называемая кельвином (К), выбрана равной одному градусу по шкале Цельсия:
1 К = 1 °С. (25.5)
Абсолютный нуль температуры. В левой части уравнения все величины могут иметь только положительные значения или быть равными нулю. Поэтому абсолютная температура T может быть только положительной или равной нулю. Температура, при которой давление идеального газа при постоянном объеме должно быть равно нулю, называется абсолютным нулем температуры.
Тепловое равновесие. Равновесные состояния и процессы. Модель идеального газа. Уравнение состояния идеального газа (уравнения Клапейрона и Клапейрона – Менделеева). Изопроцессы.
Тепловое равновесие - состояние термодинамической систем, в которое она самопроизвольно переходит через достаточно большой промежуток времени в условиях изоляции от окружающей среды. В состоянии термодинамического равновесия: - в системе прекращаются все необратимые процессы, связанные с изменением энергии: теплопроводность, диффузия, химические реакции и др.; - макроскопические параметры системы не меняются со временем.
Равнове́сный тепловой процесс — тепловой процесс, в котором система проходит непрерывный ряд бесконечно близких равновесных термодинамических состояний.
Равновесный тепловой процесс называется обратимым, если его можно провести обратно и в телах, окружающих систему, не останется никаких изменений.
Примеры равновесных процессов:
Изотермический процесс, при котором температура системы не изменяется (T=const)
Изохорный процесс, происходящий при постоянном объёме системы (V=const)
Изобарный процесс, происходящий при постоянном давлении в системе (P=const)
Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.
Свойства идеального газа на основе молекулярно-кинетических представлений определяются исходя из физической модели идеального газа, в которой приняты следующие допущения:
объём частицы газа равен нулю (то есть, диаметр молекулы
пренебрежимо
мал по сравнению со средним расстоянием
между ними, 
);импульс передается только при соударениях (то есть, силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях);
суммарная энергия частиц газа постоянна (то есть, нет передачи энергии за счет передачи тепла или излучения)
Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
Где
— молярный
объём,
Так
как 
,
где 
— количество
вещества,
а 
,
уравнение состояния можно записать:
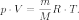
В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме
p = (γ − 1)ρε,
где 
— показатель
адиабаты, 
—
внутренняя энергия единицы массы
вещества.
Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём илитемпература — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии —изоэнтропийный (например, обратимый адиабатический процесс).
Изобарный процесс (др.-греч. ισος, isos — «одинаковый» + βαρος, baros — «вес») — процесс изменения состояния термодинамической системы при постоянном давлении (P = const)
— Закон
Гей-Люссака
'Изохорный процесс (от греч. хора — занимаемое место) — процесс изменения состояния термодинамической системы при постоянном объёме (V = const). Для идеальных газов изохорический процесс описывается законом Шарля: для данной массы газа при постоянном объеме, давление прямо пропорционально температуре:
— закон Шарля (второй
закон Гей-Люссака, 1808 г.)
Изотермический процесс (от греч. «термос» — тёплый, горячий) — процесс изменения состояния термодинамической системы при постоянной температуре (T = const).
При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const.
— закон
Бойля — Мариотта