Анализ модели и настройка регулятора

Построим частотные характеристики системы с ненастроенным регулятором (k_п=1). Будем использовать разомкнутую систему, для этого разомкнем цепь обратной связи, удалив связь клавишей [Delete] и проведем анализ. Оценим полученные характеристики системы. Выполним команду Расчеты – Характеристики.

Чтобы подробно изучить характеристики в полноэкранном режиме нужно нажать на одну из четырех кнопок [Home], [End], [PageUp] и [PageDown]. Для получения подробной информации по любому из трёх графиков, необходимо щёлкнуть правой кнопкой мыши в поле одного из них и в появившемся меню воспользоваться пунктом показатели качества (сводка) [Ctrl+I]. На экране появится окно, с информацией, соответствующей графику.

Частотные характеристики данной САУ с ненастроенным регулятором (k_п=1), построенные в программе CLASSIC представлены на рис.3

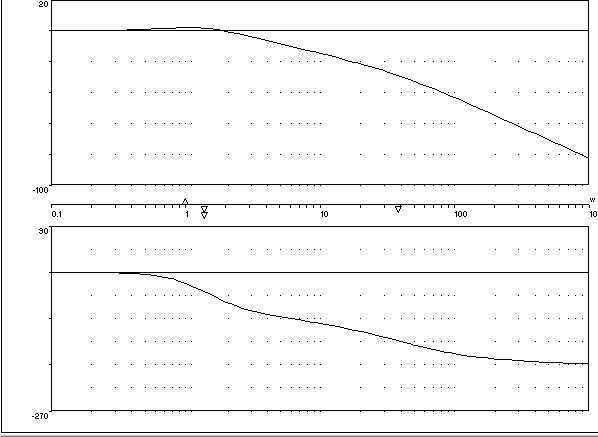
Рис.3 Логарифмические частотные характеристики системы с ненастроенным регулятором.

Подборкой числовых значений коэффициента k_п, определяем, что наиболее приемлемым будет значение k_п = 0.12, так как при нем система достигает наиболее оптимальных показателей. Исследовав систему регулирования с близлежащими значениями коэффициента усиления пропорционального канала ПД-регулятора, убеждаемся, что в другом случае переходная характеристика или имеет большую длительность переходного процесса, или колебательный процесс с перерегулированием.

Рассчитаем значение коэффициента дифференциального каналов регулятора при k_п = 0,23.

По формул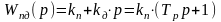е: , где  постоянная времени регулятора, k_п = 0,12 , его мы нашли методом подбора, тогда

= ∙ = 0.12∙15.8 = 1.896

Принимаем найденные настройки ПД-регулятора k_п=0,12 и k_д =1.896.

График переходного процесса с настроенным регулятором отображен на рис. 4, а ЛАХ и ЛФХ на рис. 5.

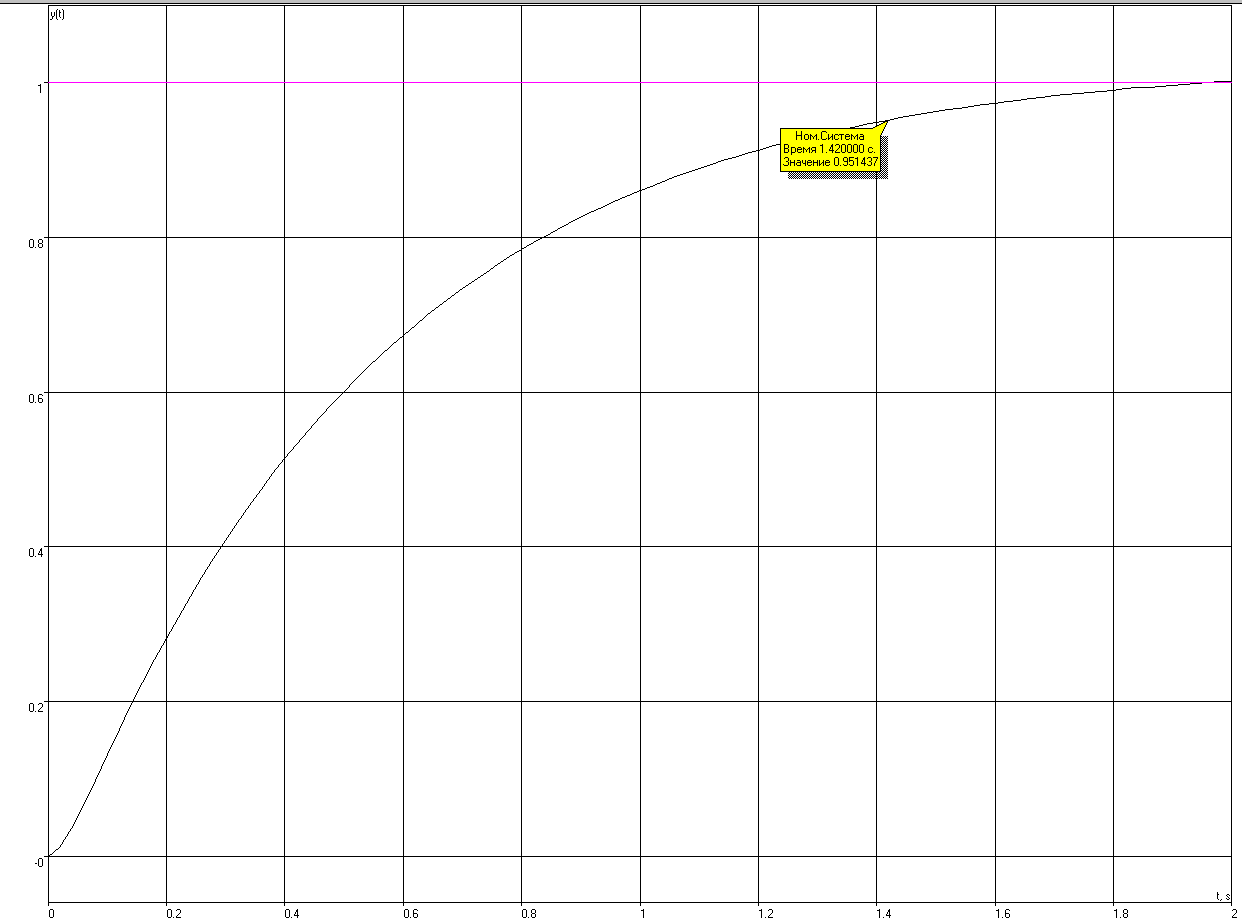
Рис.4 Переходный процесс САУ с настроенным регулятором

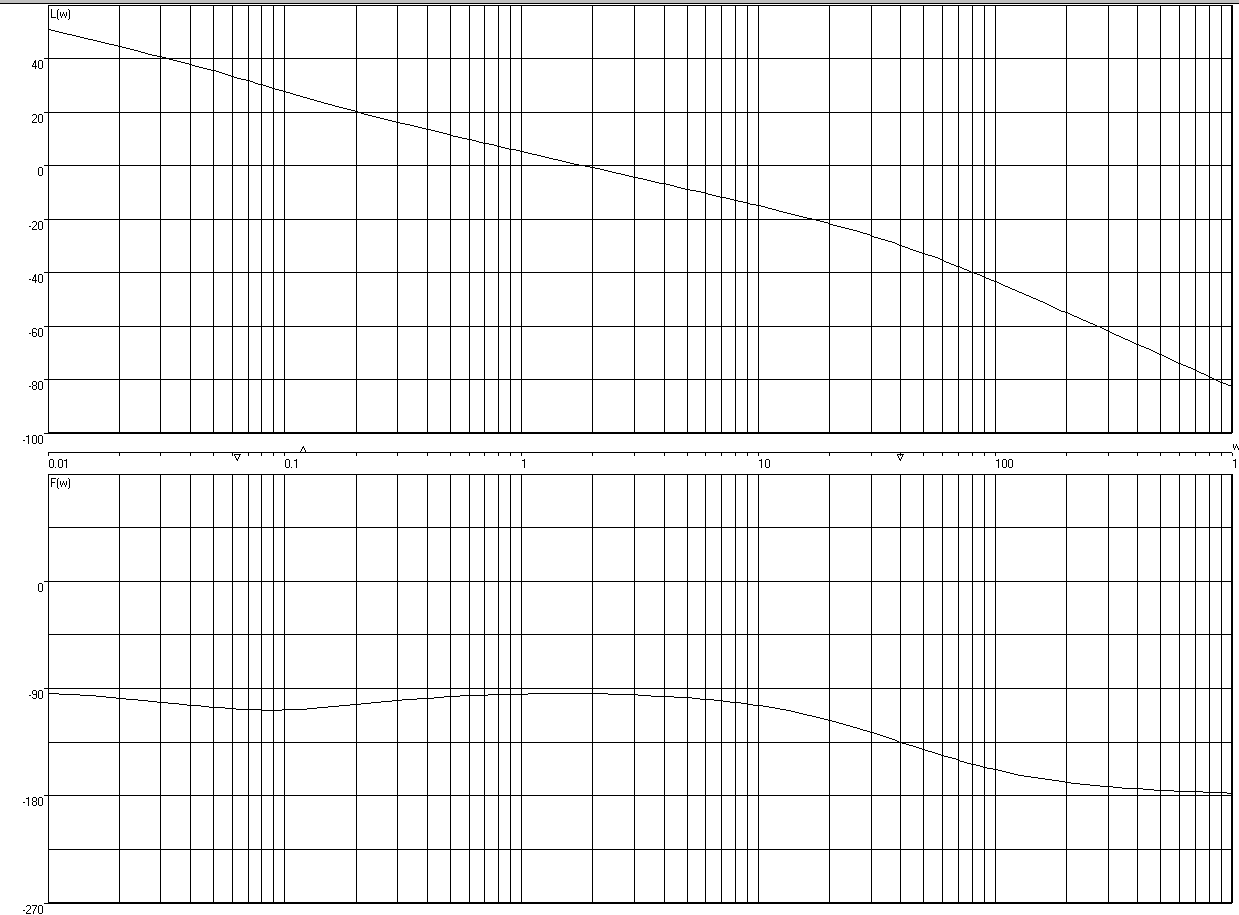
Рис.5 Логарифмические частотные характеристики системы с настроенным регулятором

Оценка качества, расчет запаса устойчивости полученной системы по логарифмическим характеристикам и графику переходного процесса.

Пользуясь частотными характеристиками настроенной системы и их показателями качества, рассчитанными в программе CLASSIC, оценим качество и запас устойчивости системы.

Модель: "C:\laba.MDL"

=======================

Ном.Система

Частота среза: 1.8154

Запас по фазе: 85.6163

Рис. ---

Частота среза системы ω_с=1.8154 с^-1. Наклон ЛАХ в пределах ±0.6 дек от ω_c равен -20 дБ/дек (рис.9), что означает, что переходный процесс в системе будет плавным, апериодическим, без перерегулирования.

Чтобы система обладала достаточным качеством, запас устойчивости по фазе должен быть не менее , а запас по амплитуде должен быть не менее .

Запас устойчивости по фазе (рис.10):

такое значение говорит о том, что система обладает достаточным качеством.

Модель: "C:\laba.MDL"

=======================

Ном.Система

Установившееся значение: 1.0000

Время регулирования: 1.4102 с

Перерегулирование: 2.24%

Рис. 11. Показатели качества переходного процесса системы.

По графику переходного процесса (рис.8) и показателям его качества (рис.11) можно заключить, что переходный процесс в системе плавный, апериодический, отсутствует перерегулирование, время за которое достигается установившееся значение процесса t_п.п.1.4102 с.