Решение системы укороченных уравнений при

Исследование системы уравнений (2.30) показало, что для случая =0, можно выбрать величину чисто действительной, а - чисто мнимой [4].

Тогда эти уравнения примут вид

(2.36)

(2.37)

Умножаем первое на , второе на и складываем, получаем

(2.38)

Первый интеграл уравнения

(2.39)

Подставляем первый интеграл в уравнение (2.37)

(2.40)

Решение (2.40) при граничной задаче :

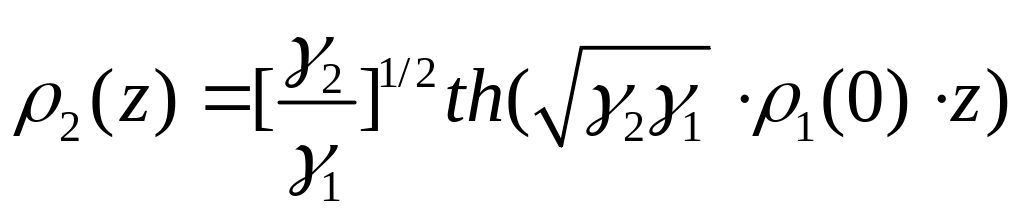(2.41)

и для поля на основной частоте имеем

(2.42)

Длина эффективного нелинейного преобразования в этом случае определяется выражением

(2.43)

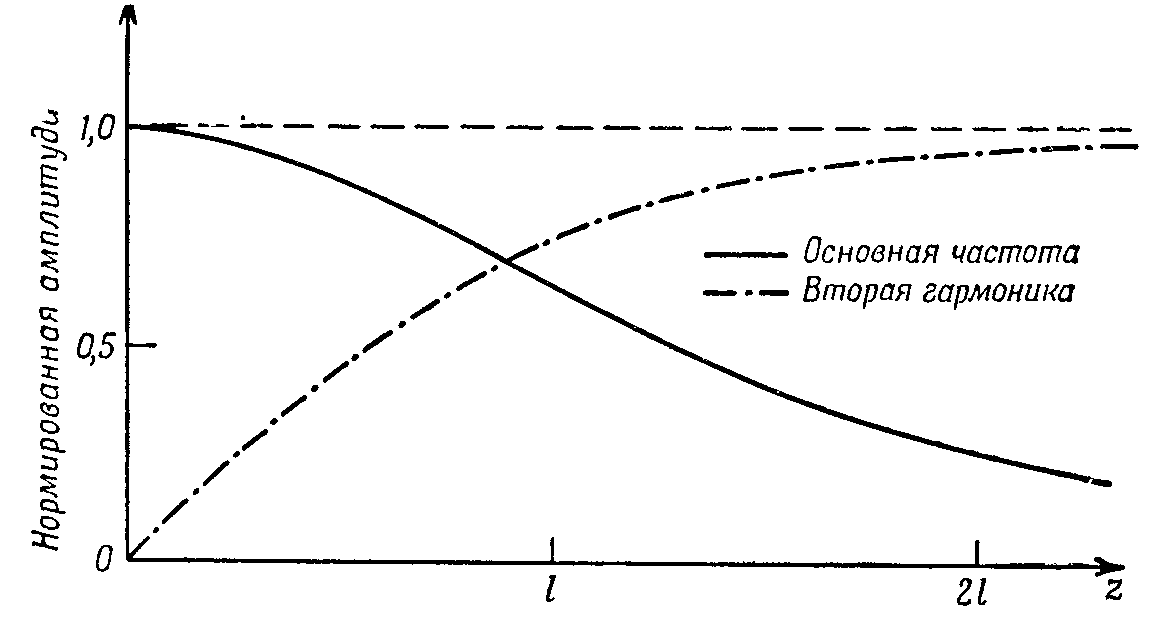
Рис.2.32. Амплитуды волн на основной частоте и частоте второй гармоники при точном фазовом согласовании.

Генерация второй гармоники в поле сверхкоротких импульсов [5]

Первое приближение теории дисперсии

Сверхкороткий оптический импульс (волновой пакет) при распространении в среде с квадратичной нелинейностью приводит к появлению в ней нелинейной поляризации P⁽²⁾ на удвоенной частоте 2₁. Нелинейная поляризация является источником волнового пакета с несущей частотой, равной 2₁.

Пренебрегая потерями в среде, взаимодействие полей в первом приближении теории дисперсии можно описать укороченными волновыми уравнениями для огибающих полей на частотах ₁ и 2₁

, (2.44)

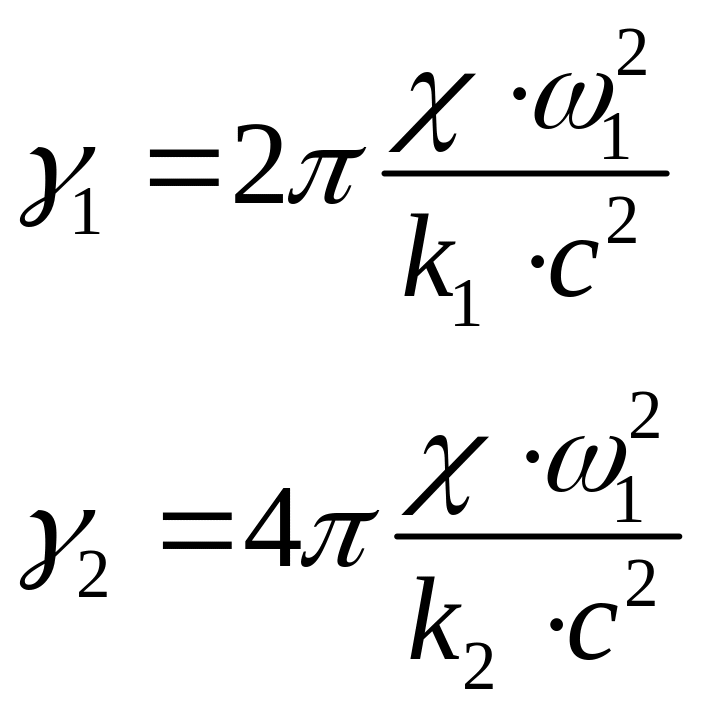где и

Квазистатический режим: ГВГ при групповом u₁= u₂ = u и фазовом синхронизмах k=0

Если в нелинейной среде выполняется условие группового u₁= u₂= u и фазового k=0 синхронизмов, то в бегущей системе координат =t-z/u решение уравнения

(2.45)

для вещественных амплитуд и фаз имеет вид:

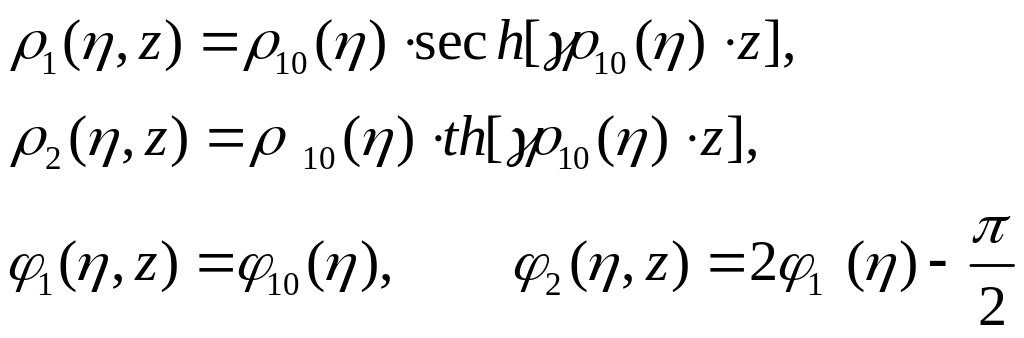. (2.46)

При генерации второй гармоники (ГВГ) фемтосекундными импульсами в условиях выполнения фазового и группового синхронизмов процесс взаимодействия полностью аналогичен ГВГ монохроматическими плоскими волнами.

Рис. 2.33. Зависимость относительных амплитуд на основной частоте и частоте второй гармоники от длины среды для различных значений параметра l_нл =1/( ₁₀): 1- 0.25 см; 2- 0.5 см; 3 - 1 см.

Приближение заданного поля в квазистатическом режиме

ρ₁(𝜂)=const

Для поля ГВГ в этом случае имеем

(2.47)

Откуда следует, что длительность импульса ГВГ короче, чем длительность основного излучения.

Для импульса гауссовой формы

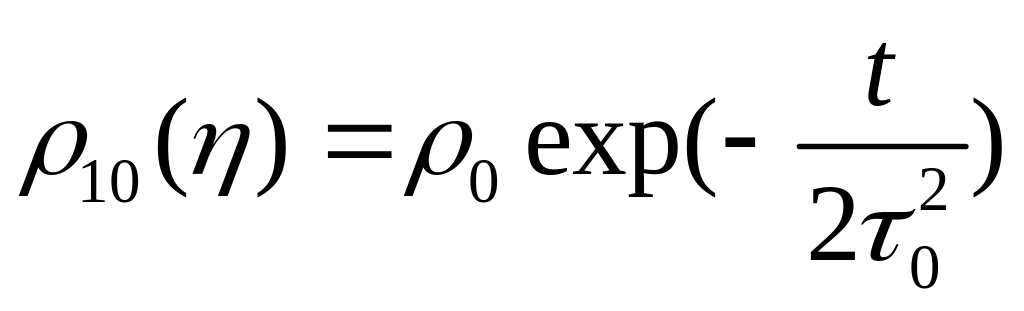(2.48)

длительность короче в раз

(2.49)

С ростом коэффициента преобразования во вторую гармонику длительность ₂ нарастает, приближаясь к ₁.

Эффект группового запаздывания: u₁≠ u_2.

Зависимость групповой скорости от частоты приводит к тому, что импульс второй гармоники смещается во времени относительно импульса нелинейной поляризации, распространяющегося с групповой скоростью, равной групповой скорости импульса на основной частоте. В этом заключается эффект группового запаздывания. Возможно как опережение, так и отставание импульса второй гармоники относительно импульса основного излучения.

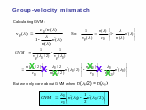
Если групповые скорости импульса основного излучения и второй гармоники не равны между собой, то величина рассогласования определяется двумя параметрами:

групповой расстройкой

(2.50)

и длиной группового запаздывания

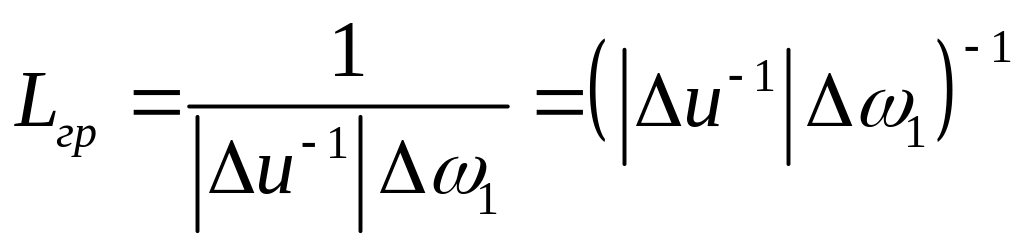(2.51)

где ₁ – ширина спектра импульса основного излучения.

Для спектрально-ограниченного импульса ₁₁1, поэтому длина группового запаздывания определяется выражением

(2.52)

Если длина группового запаздывания больше длины взаимодействия, L_гр>z, то групповая расстройка не сказывается на процессе преобразования основного излучения в ВГ, и процесс удвоения идет также, как и в условиях группового синхронизма, т.е. в квазистатическом режиме.

В связи с этим длину группового запаздывания L_гр определяют, как длину квазистатического режима генерации второй гармоники.

Если длина группового запаздывания меньше длины взаимодействия, L_гр<z, то процесс удвоения проходит в нестационарном режиме.

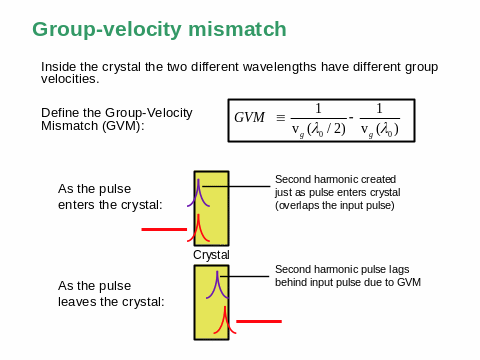
Приближение заданного поля в нестационарном режиме

Если в процессе нелинейного взаимодействия амплитуда и фаза на основной частоте мало изменяются, то можно принять, что A₁(t,z)=const и система (2.44) принимает вид

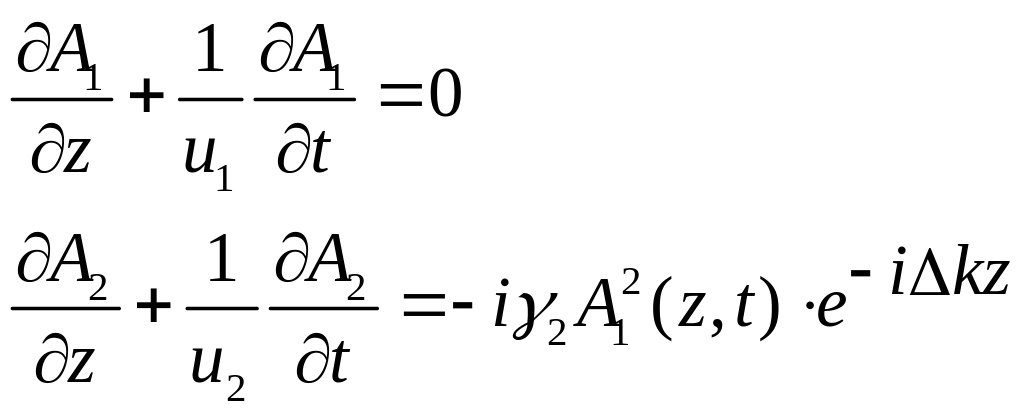(2.53)

Решение первого уравнения есть .

Переходя к переменной 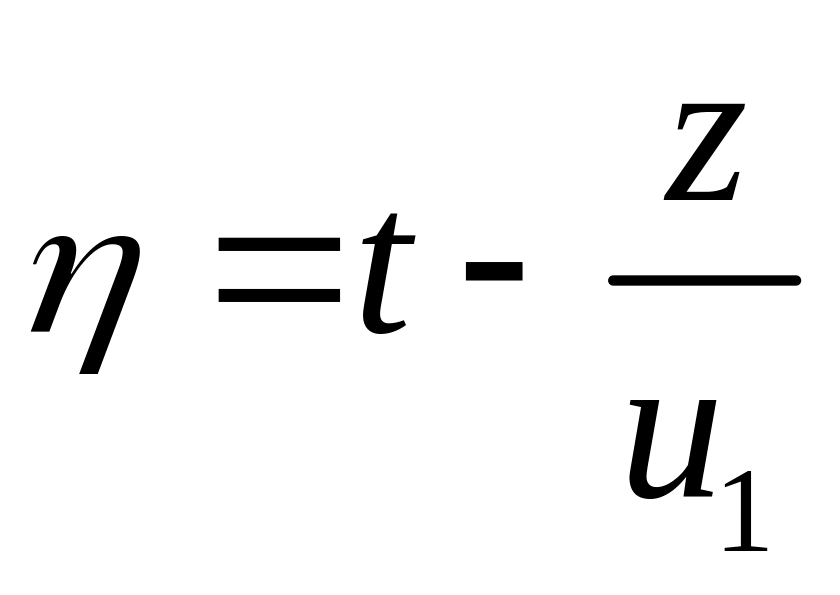во втором уравнении системы (2.53)

имеем

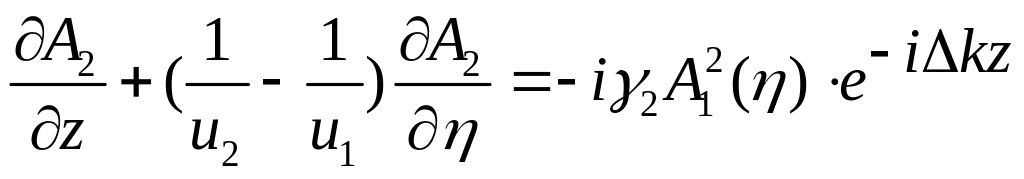(2.54)

где - групповая расстройка.

Спектральный подход к решению задачи о нестационарной ГВГ [3]

Для импульса основного излучения с гауссовой формой временной огибающей вида

(2.60)

спектр второй гармоники будет иметь вид

(2.66)

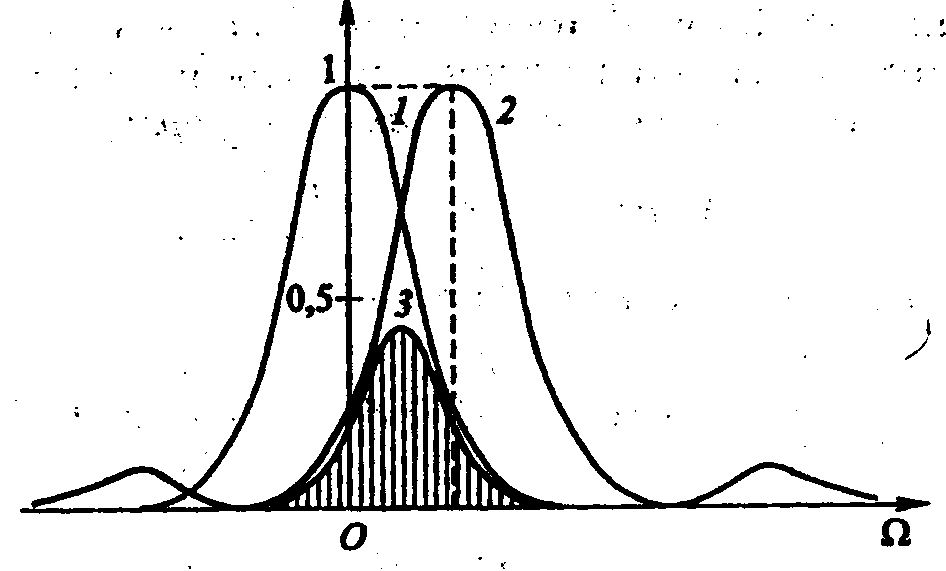
.Рис.2.35. 1- спектр основного излучения , 2 - , 3 -

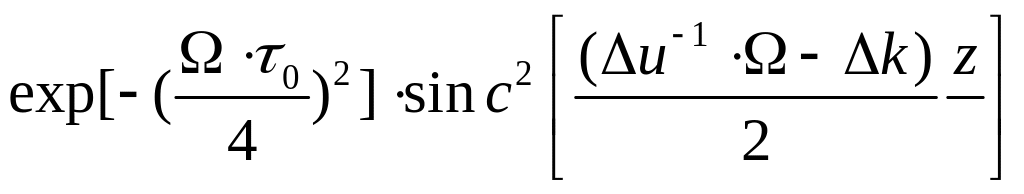
Спектр ГВГ искажен по сравнению со спектром основного излучения:

1 - гауссово распределение модулируется функцией sinc²,

2 - максимум спектра смещается по частоте.

Смещение максимума спектра ГВГ

Величину смещения максимума спектрального распределения второй гармоники можно оценить, воспользовавшись приближенным соотношением

(2.67)

при этом происходит потеря боковых максимумов функции sinc²(φ z/2).

В этом приближении для спектра ВГ получаем следующее выражение

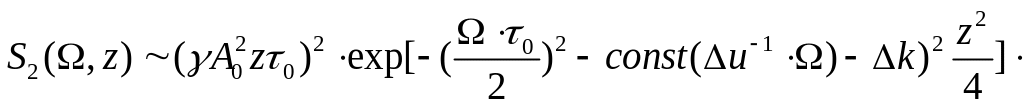. (2.68)

Дифференцируя его по  и приравнивая производную нулю, находим частоту максимума спектра ВГ _max .

Тогда имеем (c=const)

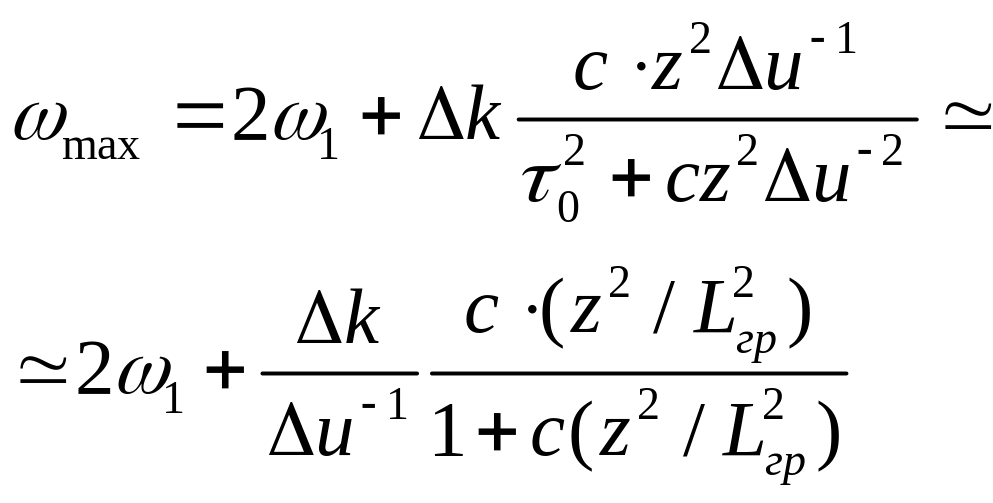, (2.69)

где 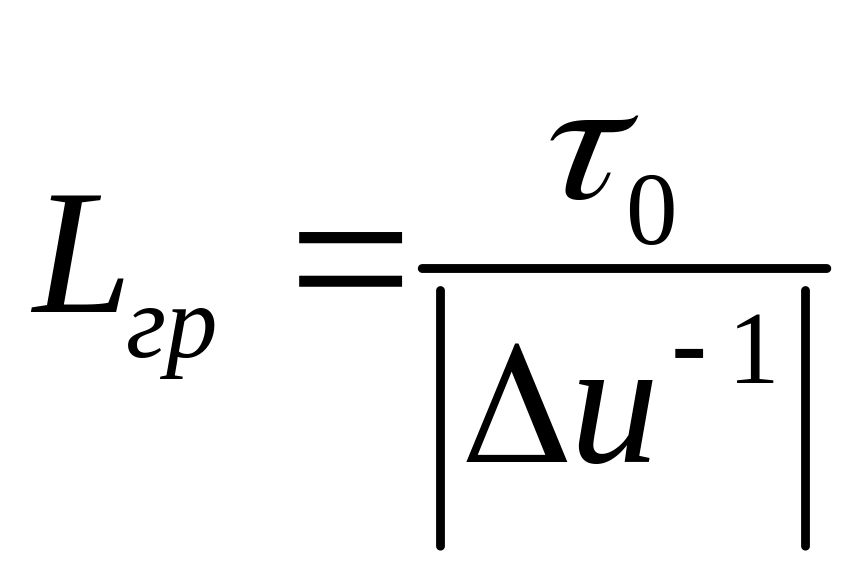длина группового запаздывания или длина квазистатического взаимодействия (при z< L_гр )

При >>1 величина сдвига максимума спектрального распределения второй гармоники определяется величиной k , которую можно менять, изменяя угол падения на кристалл или его температуру

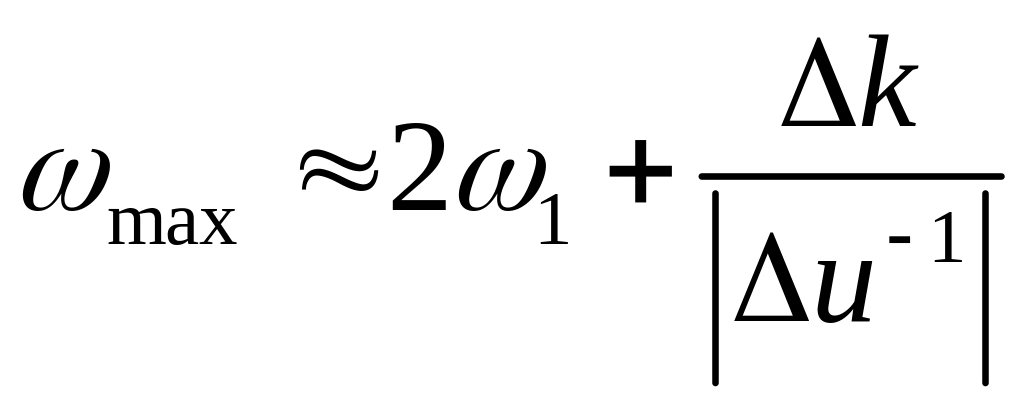. (2.70)