
Одноосные кристаллы
Для
оптических кристаллов с
![]() УрФ распадается
на два, так что одна поверхность показателя
преломления обыкновенной
(ordinary) волны –
поверхность сферы радиуса
УрФ распадается
на два, так что одна поверхность показателя
преломления обыкновенной
(ordinary) волны –
поверхность сферы радиуса
![]() ,
где
,
где
![]() ,
а другая – поверхность эллипсоида
вращения вокруг оптической оси z
- поверхность необыкновенной
(extrzordinary) волны:
,
а другая – поверхность эллипсоида
вращения вокруг оптической оси z
- поверхность необыкновенной
(extrzordinary) волны:
 ,
где
,
где
![]() и - угол
от оси Z.
(2.17)
и - угол
от оси Z.
(2.17)
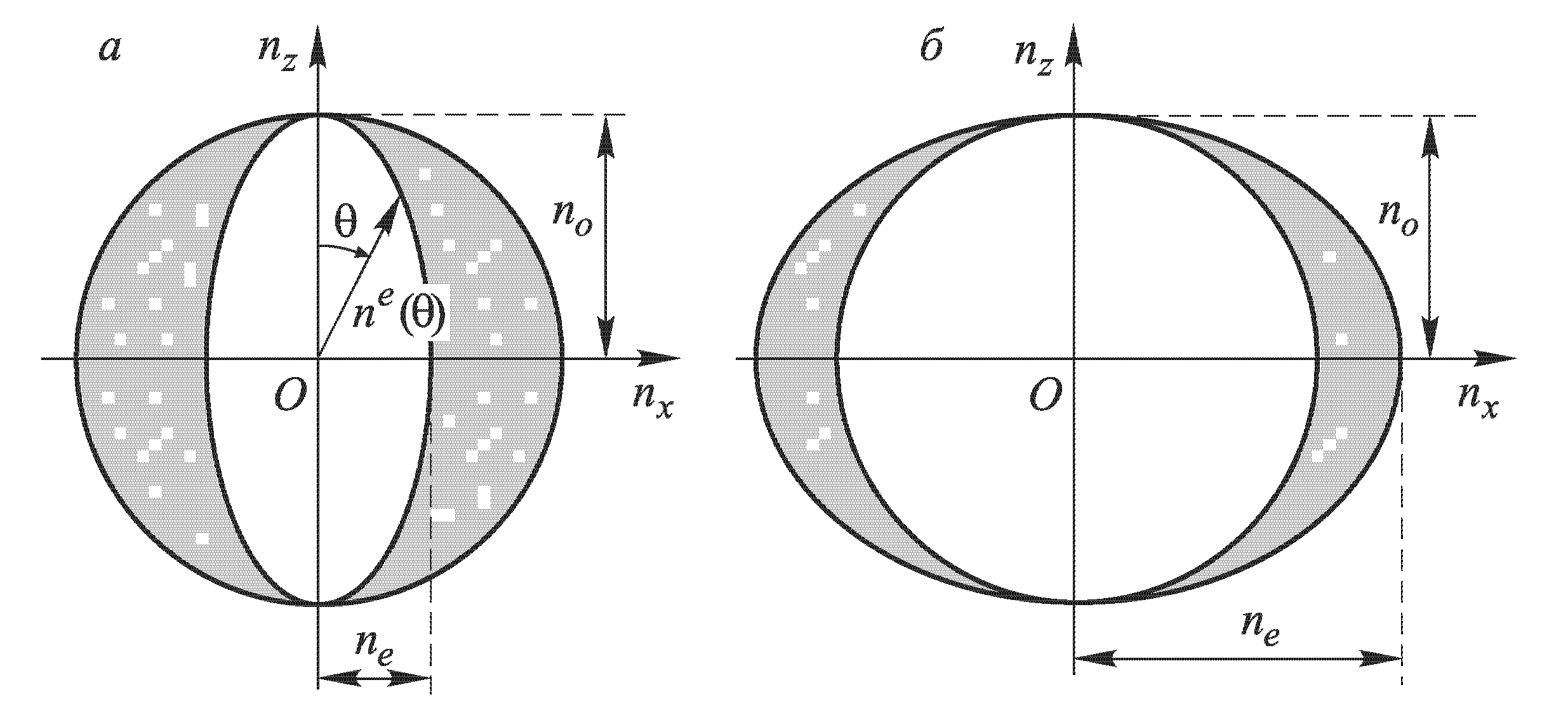
Рис.2.24. Сечения поверхностей показателей преломления одноосных кристаллов:
отрицательного no> ne и (б) положительного ne > no.
Сфера и эллипсоид соприкасаются в направлении оптической оси. Плоскость главного сечения - плоскость, проходящая через оптическую ось и волновой вектор. Поляризация обыкновенной волны - перпендикулярна этой плоскости, а необыкновенной - лежит в ней.
Преломление на границе одноосного кристалла. Двулучепреломление.
Особенности преломления на границе анизотропного кристалла и распространения в нем:
в общем случае на границе происходит двойное лучепреломление,
двойное лучепреломление может происходить даже при нормальном падении на границу,
преломленный необыкновенный луч всегда лежит в главной плоскости,

Рис.2.26. Распространение поляризованного света вдоль главных осей одноосного кристалла

Рис. 2.27. Четвертьволновая пластинка
Генерация второй гармоники (общие положения) [3]
Источником в процессе ГВГ является нелинейная квадратичная поляризация:
![]() (2.20)
(2.20)
где запись сделана
в условно-векторном виде через
восприимчивость![]() ,
которая является тензором третьего
ранга.
,
которая является тензором третьего
ранга.
В общем случае ГВГ описывается двумя соотношениями:
![]() и
и
![]() .
.
Соотношение
для волновых векторов
![]() фактически является условием фазового
согласования для процесса ГВГ, т.е.
синхронного взаимодействия при
распространении с равными фазовыми
скоростями волны второй гармоники и ее
источника - нелинейной поляризации
(фазовая скорость основной частоты).
фактически является условием фазового
согласования для процесса ГВГ, т.е.
синхронного взаимодействия при
распространении с равными фазовыми
скоростями волны второй гармоники и ее
источника - нелинейной поляризации
(фазовая скорость основной частоты).
Условия фазового согласования ГВГ в одноосных кристаллах
В простейшем случае при коллинеарном взаимодействии условие фазового синхронизма
приводит к равенству:
![]() или
или
![]() . (2.21)
. (2.21)


Сечения
поверхностей показателя преломления
отрицательного одноосного кристалла
для основной частоты и второй гармоники
показывают, что условие (2.21) выполняется
для
![]() :
:
![]() :
:

Рис.2.29. Сечения поверхностей показателя преломления отрицательного одноосного кристалла для основной частоты (штриховка) и второй гармоники (заливка).
ГВГ в приближении плоских монохроматических волн
Распространение волнового пакета с напряженностью поля E(t,z) в нелинейной квадратичной среде, считая, что E(t,z) не зависит от поперечных пространственных координат, описывается волновым уравнением с нелинейной правой частью:
![]() (2.25)
(2.25)
Считая, что выполняется условие медленно меняющихся амплитуд как по времени, так и по пространственным координатам, ограничимся рассмотрением только плоских монохроматических волн на основной частотой ω и частоте второй гармоники 2 со стационарными амплитудами. Тогда поле в среде представляем в виде суперпозиции этих полей:
![]() (2.26)
(2.26)
Оставим только члены с частотами ω и 2ω
![]() (2.27)
(2.27)
С учетом (2.27) уравнение (2.25) примет вид
![]() (2.28)
(2.28)
Так как левая часть уравнения линейна по полю, то его можно разбить на два уравнения, приравняв члены с частотами ω и 2ω в левой и правой его частях:
![]() (2.29а)
(2.29а)
![]() (2.29б)
(2.29б)
Пренебрегая вторыми производными в рамках приближения ММА и считая, что отсутствует поглощение, получаем систему укороченных уравнений :
![]() (2.30а)
(2.30а)
![]() (2.30б)
(2.30б)
где
![]() ,
,
![]() и
и
![]()
Решение системы в приближении заданного поля основной частоты (A1=const) при граничной задаче: A2 (0) =0:

или
 (2.31)
(2.31)
переходя к действительным амплитудам, имеем
![]() (2.32)
(2.32)
При
![]() =0
амплитуда растет линейно по z.
Длина, на которой амплитуда
=0
амплитуда растет линейно по z.
Длина, на которой амплитуда
![]() достигает
достигает
![]() ,
называется длиной нелинейного
взаимодействия или длиной эффективного
преобразования,
,
называется длиной нелинейного
взаимодействия или длиной эффективного
преобразования,
![]() (2.33)
(2.33)
При
≠0
амплитуда гармоники испытывает
пространственные биения как
![]() .
Длина, на которой амплитуда гармоники
достигает mаx
называется длиной когерентности
процесса ГВГ:
.
Длина, на которой амплитуда гармоники
достигает mаx
называется длиной когерентности
процесса ГВГ:
![]() и
и
![]() (2.34)
(2.34)
Для плоских волн при заданном поле на основной частоте выражение для интенсивности ГВГ будет иметь вид
 (2.35)
(2.35)
Полученную
зависимость
![]() от
от
![]() называют кривой синхронизма
-
называют кривой синхронизма
-![]() .
.

Рис.2.31. Кривая синхронизма ГВГ
Угловая
отстройка от угла синхронизма приведет
к возрастанию
.
При значении
![]()
![]() и
и
![]() .
На этом уровне
0.41 от максимума ширина кривой синхронизма
равна π в единицах
.
На этом уровне
0.41 от максимума ширина кривой синхронизма
равна π в единицах
![]() .
.


