II. Квадратичные по полю эффекты при взаимодействии фемтосекундных оптических импульсов с материальными средами

2.3. Генерация второй гармоники в анизотропной дисперсионной среде: кристаллооптика анизотропной среды, укороченные волновые уравнения, фазовый и групповой синхронизмы, приближение заданного поля, стационарный и нестационарный режимы генерации второй гармоники [1-5]

Генерация второй гармоники (ГВГ или SHG) является нелинейно-оптическим процессом, который, так же как и оптическое выпрямление, в дипольном приближении разрешен только в средах без центра инверсии.

Так как согласно принципу Неймана элементы симметрии кристалла должны являться элементами симметрии его физического свойства, то тензора, описывающие то и иное свойство кристалла, должны подчиняться этим элементам симметрии. Это налагает значительные ограничения на число ненулевых компонент тензоров различных рангов и на возможность проявления этого свойства в кристаллах. Наличие в наборе операций симметрии кристалла, например, центра инверсии, приводит к тому, что процессы, описываемые тензорами нечетного ранга, в этих кристаллах не проявляются, так как их все компоненты тождественно должны быть равными нулю.

Диэлектрическая проницаемость является симметричным тензором второго ранга, который всегда может быть приведен к главным осям, где он имеет диагональный вид (если поглощения нет).

С учетом свойств симметрии, этот тензор может иметь следующие три соотношения между диагональными элементами:

- - три не равных диагональных элемента – оптически двуосные кристаллы;

- - два не равных диагональных элемента – оптически одноосные кристаллы;

- - три равных друг другу элемента – оптически изотропные кристаллы.

Что касается оптических свойств кристаллов, то они описываются, как хорошо известно, диэлектрической проницаемостью - .

В общем случае в плоской волне, распространяющейся в анизотропной среде, вектор D∦E, т.к.

, (2.12)

и из уравнений Максвелла для плоской волны с следует следующая ориентация векторов:

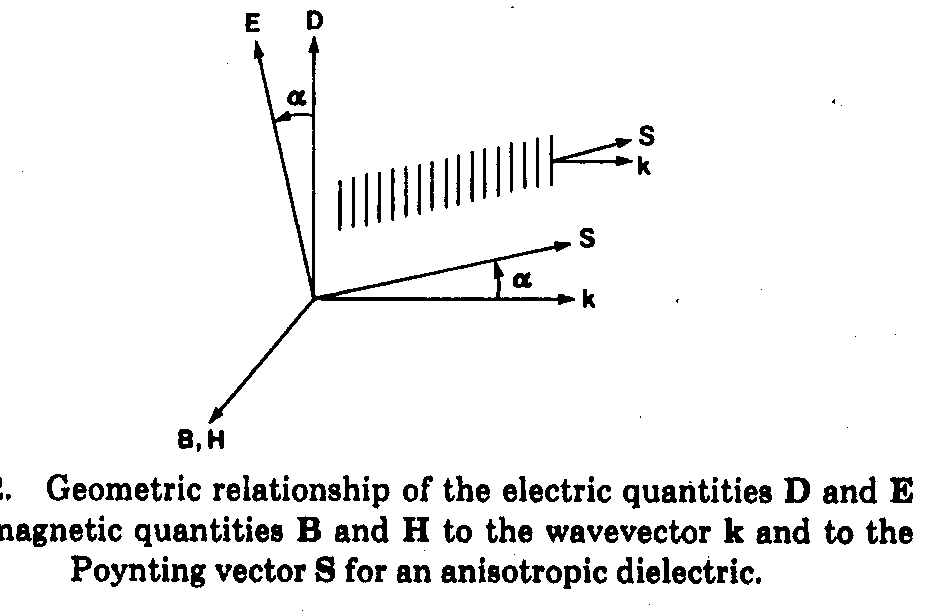
Рис. 2.22. Ориентация векторов волны в анизотропной среде.

Таким образом, k, D и H взаимно перпендикулярны, H перпендикулярен E, т.е. k, D и E лежат в одной плоскости. Направление плотности

потока энергии s не совпадает с направлением волнового вектора k, не совпадают также направления фазовой и групповой скоростей.

Для описания оптически свойств анизотропных кристаллов используется два представления. Одно из них (более старое) базируется на введении понятия оптической индикатрисы, второе - на решениях уравнения Френеля.

Уравнение Френеля [2,3]

Из уравнения Максвелла для немагнитной непроводящей среды, в которой распространяется плоская электромагнитная волна

(2.13)

нетрудно получить уравнение Френеля (УрФ), введя единичный вектор , перпендикулярный к волновому фронту , и, исключая из первого уравнения Максвелла,

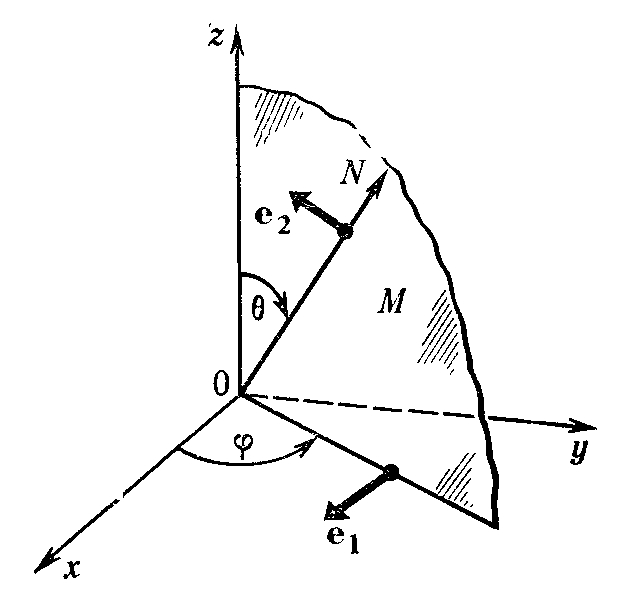
Рис.2.23. Определение плоскости главного сечения: ON – направление вектора k, М - плоскость главного сечения.

имеем , (2.14)

откуда, используя правило AxBxC=ВАС-САВ и заменяя на , получим

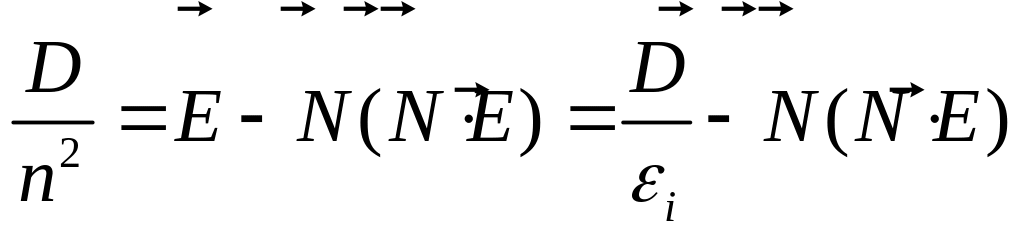, (3.15)

образуя скалярное произведение , которое в силу ортогональности равно нулю, получим уравнение Френеля:

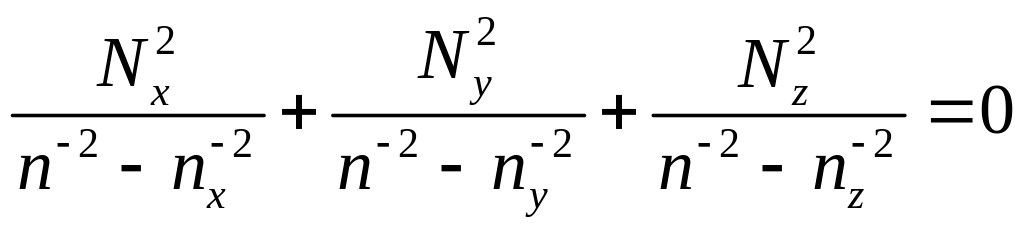(2.16)

УрФ позволяет определить, как зависит показатель преломления в кристалле с заданными главными значениями от направления вектора .

В общем случае (2.16) – квадратное уравнение относительно n². Двум независимым положительным решениям УрФ и соответствуют два значения вектора электрической индукции D₁ и D₂, скалярное произведение которых при использовании УрФ показывает, что оно будет тождественно равно нулю. Это означает, что D₁ и D₂ ортогональны, и им соответствуют разные по величине показатели преломления.

Таким образом, в общем случае, в анизотропной среде волна распространяется в виде двух волн с одинаковыми частотами, но с ортогональными поляризациями и с разными скоростями (любая волна расщепляется на две этих волны). В этом случае решение УрФ представляет двухполостную поверхность, которую можно назвать поверхностью показателей преломления или поверхностью волновых векторов.