- •Программирование на языках высокого уровня. Алгоритмические языки
- •Содержание
- •Разработка (проектирование) одномодульных программ
- •Представление информации в языке Си
- •Массивы
- •УказатеЛи
- •Выражения и операции
- •Управляющие операторы
- •Функции
- •Типы данных, определяемые пользователем
- •Приемы программирования
- •Приложение 2. Арифметические основы компьютеров
- •Литература
Приемы программирования
Динамические структуры данных
Во многих реальных задачах необходимо работать с большими заранее неизвестными объемами данных. Использование статических структур данных (например, массивов) в этих случаях неэффективно по следующим причинам. Во-первых, не всегда можно определить верхнюю границу объема данных. Во-вторых, если такая граница существует, это не означает, что реально будет обрабатываться именно максимальное количество информации, т.е. будет наблюдаться перерасход памяти.
Например, в некоторых задачах используются матрицы, имеющие треугольный вид:
|
|
0 |
1 |
2 |
3 |
|
0 |
1 |
3 |
5 |
6 |
|
1 |
|
4 |
9 |
7 |
|
2 |
|
|
2 |
8 |
|
3 |
|
|
|
0 |
Реализация треугольной матрицы в виде двумерного массива целых чисел размерностью 100×100 элементов приведет к перерасходу памяти в размере 4*(10000 – N*(N+1)/2) байт, где N – фактический размер матрицы. Если N = 4, то потери памяти составят 4*(10000 – 4*(4+1)/2) = 4*9990 = 39964 байт.
Для более эффективного хранения информации используются динамические структуры данных, память под которые выделяется и освобождается по мере необходимости. В языке Си для выделения памяти используются библиотечные функции malloc(), calloc() и realloc(), а в языке Си++ добавляется операция new. Если данные становятся ненужными, то память освобождается c помощью функции free()(в языке Си) или операции delete (в языке Си++).
Сначала рассмотрим библиотечные функции malloc(), calloc(), realloc() и free(), которые объявляются в заголовочном файле <stdlib.h>.
|
Прототип функции |
Описание функции |
|
void *malloc( size_t size ); |
Выделяет непрерывный блок памяти размером size байт. Возвращает либо адрес выделенного блока памяти, либо NULL, если память не выделена |
|
void *calloc( size_t num, size_t size ); |
Выделяет массив из num элементов размером size байт каждый. Возвращает либо адрес выделенного блока памяти, либо NULL, если память не выделена |
|
void *realloc( void *memblock, size_t size ); |
Расширяет или сокращает блок памяти memblock до новых размеров size. Возвращает либо адрес вновь выделенного блока памяти, либо NULL, если память не выделена. Если новый блок памяти выделяется успешно, то старый освобождается автоматически. Содержимое блока памяти сохраняется, на сколько это возможно. |
|
void free( void *memblock ); |
Освобождает память, занимаемую выделенным блоком памяти. |
Применим рассмотренные выше функции для создания динамического целочисленного массива. В таком массиве память под элементы изначально не выделяется; она будет выделена только после того, как станет известно (например, задаст пользователь) фактическое количество элементов массива MassSize. Для реализации динамического массива необходимо объявить указатель Mass, в котором будет храниться адрес выделенного блока памяти.
int *Mass; // указатель на первый элемент массива
int MassSize; // кол-во элементов массива
int i; // индекс эл-та массива
// Запрашиваем кол-во эл-тов массива и создаем массив заданной длины
printf("\nInput mass size= ");
scanf("%d", &MassSize);
Mass= (int *)calloc(MassSize, sizeof(int));
//Mass= (int *)malloc(MassSize*sizeof(int));
// Заполняем массив значениями
for(i= 0; i < MassSize; i++)
{ Mass[i]= i; }
// Распечатываем содержимое массива
for(i= 0; i < MassSize; i++)
{ printf("%d ", Mass[i]); }
// Уничтожаем массив
free(Mass);
Обратите внимание, что при выделении памяти используется операция sizeof(), она возвращает кол-во байт, которое занимает тип данных int. В общем случае данная операция имеет следующий формат:
sizeof(<тип данных>) или sizeof(<переменная>)
Наряду с библиотечными функциями malloc(), calloc(), realloc() и free() в языке Си++ используются операции new и delete. С помощью операции new происходит выделение памяти; если по каким-либо причинам память не может быть выделена, то операция возвращает NULL. Операция имеет два формата – один для скалярных типов данных, а другой для массивов:
<переменная-указатель> = new <тип данных>
<переменная-указатель> = new <тип данных>[<кол-во элементов>]
Для освобождения памяти используется операция delete. Она также имеет два формата:
delete <переменная-указатель>
delete[] <переменная-указатель>
Приведем вариант реализации динамического массива с использованием операций new и delete.
int *Mass; // указатель на первый элемент массива
int MassSize; // кол-во элементов массива
int i; // индекс эл-та массива
// Запрашиваем кол-во эл-тов массива и создаем массив заданной длины
printf("\nInput mass size= ");
scanf("%d", &MassSize);
Mass= new int[MassSize];
// Заполняем массив значениями
for(i= 0; i < MassSize; i++)
{ Mass[i]= i; }
// Распечатываем содержимое массива
for(i= 0; i < MassSize; i++)
{ printf("%d ", Mass[i]); }
// Уничтожаем массив
delete[] Mass;
Из примера видно, что операция new имеет преимущества перед библиотечными функциями malloc() и calloc(), т.к. операция сама определяет размер типа данных и возвращает типизированный указатель.
|
Окончание занятия №25 (лекция) |
Динамический массив может изменять свои размеры в процессе работы программы. В языке Си для увеличения или уменьшения массива рационально использовать функцию realloc(), которая выделяет новый блок памяти, переписывает в него данные из старого блока памяти, а затем освобождает память, занимаемую старым блоком памяти. Ниже приведен листинг программы, реализующей изменение размера динамического массива с использованием библиотечной функции realloc().
int *Mass; // указатель на первый элемент массива
int MassSize; // кол-во элементов массива
int i;
// Запрашиваем кол-во эл-тов массива и создаем массив заданной длины
printf("\nInput mass size= ");
scanf("%d", &MassSize);
Mass= (int *)calloc(MassSize, sizeof(int));
// Заполняем массив значениями
for(i= 0; i < MassSize; i++)
{ Mass[i]= i; }
// Запрашиваем новое кол-во эл-тов массива, выдяеляем для массива
// новый блок памяти заданной длины и переписываем в него имеющуюся
// информацию (насколько это возможно), освобождаем старый блок памяти,
// используемый массивом
printf("\nInput mass size= ");
scanf("%d", &MassSize);
Mass = (int *)realloc(Mass, MassSize*sizeof(int));
// Распечатываем содержимое массива
for(i= 0; i < MassSize; i++)
{ printf("%d ", Mass[i]); }
// Уничтожаем массив
free(Mass);
В языке Си++ нет операции аналогичной функции realloc(), поэтому программист должен самостоятельно реализовать действия, выполняемые функцией realloc().
int *Mass; // указатель на первый элемент массива
int MassSize; // кол-во элементов массива
int *OldMemBlock; // указатель на старый блок памяти
int OldMassSize; // старое кол-во элементов массива
int i;
// Запрашиваем кол-во эл-тов массива и создаем массив заданной длины
printf("\nInput mass size= ");
scanf("%d", &MassSize);
Mass= new int[MassSize];
// Заполняем массив значениями
for(i= 0; i < MassSize; i++)
{ Mass[i]= i; }
// Запрашиваем новое кол-во эл-тов массива
OldMassSize= MassSize;
printf("\nInput mass size= ");
scanf("%d", &MassSize);
// Выдяеляем для массива новый блок памяти заданной длины
OldMemBlock= Mass;
Mass= new int[MassSize];
// Переписываем в новый блок памяти содержимое массива из старого блока
// памяти
for(i= 0; i < min(OldMassSize, MassSize); i++)
{ Mass[i]= OldMemBlock[i]; }
// Освобождаем старый блок памяти, используемый массивом
delete[] OldMemBlock;
// Распечатываем содержимое массива
for(i= 0; i < MassSize; i++)
{ printf("%d ", Mass[i]); }
// Уничтожаем массив
delete[] Mass;
|
Окончание занятия №26 (лекция) |
Перебор и его сокращение
Имеется класс задач, которые решаются путем порождения потенциальных решений и их проверки на соответствие условиям задачи. Для примера рассмотрим следующую задачу.
Формулировка задания:
Найти все четверки элементов данного одномерного массива натуральных чисел, произведение которых равно 120.
Идея решения:
Для решения данной задачи необходимо рассмотреть подмножества исходного массива (потенциальные решения) и выбрать из них те, которые одновременно удовлетворяют двум условиям:
– подмножество состоит из четырех элементов;
– произведение элементов подмножества равно 120.
В зависимости от способа порождения потенциальных решений можно выделить несколько вариантов решения данной задачи:
– породить все возможные потенциальные решения и выбрать из них те, которые удовлетворяют условиям задачи (подмножество состоит из четырех элементов; произведение элементов подмножества равно 120);
– породить потенциальные решения с учетом имеющихся ограничений (подмножества, состоящие из четырех элементов) и выбрать из них те, которые удовлетворяют условию задачи (произведение элементов подмножества равно 120);
– породить дерево потенциальных решений с учетом имеющихся ограничений (подмножество состоит из четырех элементов; произведение элементов подмножества равно 120).
Первый вариант решения использует полный перебор потенциальных решений, а два других – сокращенный перебор. Рассмотрим подробнее каждый из вариантов решения задачи.
Реализация полного перебора
Реализация полного перебора заключается в порождении всех возможных потенциальных решений. При этом порядок их порождения не важен, главное – рассмотреть все возможные случаи решения.
Наиболее универсальный способ организации полного перебора заключается в использовании бинарного числа. Применительно к решаемой задаче бинарное число должно иметь количество разрядов, равное количеству элементов массива N. Каждый разряд такого числа показывает, включается ли соответствующий элемент массива в подмножество или нет. Например, бинарное число 01111 показывает, что потенциальное решение будут составлять первые четыре элемента массива. Таким образом, бинарные числа в диапазоне от 0 до (2N-1) соответствуют всем подмножествам исходного массива. Ниже приведена трасса поиска подмножеств для массива размерности N=5.
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5
старший
разряд |
|
Бинарное число BinaryNumber |
0 |
0 |
0 |
0 |
0 |
|
Подмножество Group |
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
1 |
0 |
0 |
0 |
0 |
|
Подмножество Group |
1 |
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
0 |
1 |
0 |
0 |
0 |
|
Подмножество Group |
|
2 |
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
1 |
1 |
0 |
0 |
0 |
|
Подмножество Group |
1 |
2 |
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
0 |
0 |
1 |
0 |
0 |
|
Подмножество Group |
|
|
3 |
|
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
1 |
0 |
1 |
0 |
0 |
|
Подмножество Group |
1 |
|
3 |
|
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
0 |
1 |
1 |
0 |
0 |
|
Подмножество Group |
|
2 |
3 |
|
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
1 |
1 |
1 |
0 |
0 |
|
Подмножество Group |
1 |
2 |
3 |
|
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
0 |
0 |
0 |
1 |
0 |
|
Подмножество Group |
|
|
|
4 |
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
1 |
0 |
0 |
1 |
0 |
|
Подмножество Group |
1 |
|
|
4 |
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
0 |
1 |
0 |
1 |
0 |
|
Подмножество Group |
|
2 |
|
4 |
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
1 |
1 |
0 |
1 |
0 |
|
Подмножество Group |
1 |
2 |
|
4 |
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
0 |
0 |
1 |
1 |
0 |
|
Подмножество Group |
|
|
3 |
4 |
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
1 |
0 |
1 |
1 |
0 |
|
Подмножество Group |
1 |
|
3 |
4 |
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
0 |
1 |
1 |
1 |
0 |
|
Подмножество Group |
|
2 |
3 |
4 |
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
1 |
1 |
1 |
1 |
0 |
|
Подмножество Group |
1 |
2 |
3 |
4 |
|
Данное подмножество состоит из четырех элементов, поэтому можно анализировать произведение его элементов: 1 * 2 * 3 * 4 ≠ 120
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
0 |
0 |
0 |
0 |
1 |
|
Подмножество Group |
|
|
|
|
5 |
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
1 |
0 |
0 |
0 |
1 |
|
Подмножество Group |
1 |
|
|
|
5 |
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
0 |
1 |
0 |
0 |
1 |
|
Подмножество Group |
|
2 |
|
|
5 |
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
1 |
1 |
0 |
0 |
1 |
|
Подмножество Group |
1 |
2 |
|
|
5 |
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
0 |
0 |
1 |
0 |
1 |
|
Подмножество Group |
|
|
3 |
|
5 |
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
1 |
0 |
1 |
0 |
1 |
|
Подмножество Group |
1 |
|
3 |
|
5 |
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
0 |
1 |
1 |
0 |
1 |
|
Подмножество Group |
|
2 |
3 |
|
5 |
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
1 |
1 |
1 |
0 |
1 |
|
Подмножество Group |
1 |
2 |
3 |
|
5 |
Данное подмножество состоит из четырех элементов, поэтому можно анализировать произведение его элементов: 1 * 2 * 3 * 5 ≠ 120
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
0 |
0 |
0 |
1 |
1 |
|
Подмножество Group |
|
|
|
4 |
5 |
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
1 |
0 |
0 |
1 |
1 |
|
Подмножество Group |
1 |
|
|
4 |
5 |
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
0 |
1 |
0 |
1 |
1 |
|
Подмножество Group |
|
2 |
|
4 |
5 |
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
1 |
1 |
0 |
1 |
1 |
|
Подмножество Group |
1 |
2 |
|
4 |
5 |
Данное подмножество состоит из четырех элементов, поэтому можно анализировать произведение его элементов: 1 * 2 * 4 * 5 ≠ 120
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
0 |
0 |
1 |
1 |
1 |
|
Подмножество Group |
|
|
3 |
4 |
5 |
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
1 |
0 |
1 |
1 |
1 |
|
Подмножество Group |
1 |
|
3 |
4 |
5 |
Данное подмножество состоит из четырех элементов, поэтому можно анализировать произведение его элементов: 1 * 3 * 4 * 5 ≠ 120
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
0 |
1 |
1 |
1 |
1 |
|
Подмножество Group |
|
2 |
3 |
4 |
5 |
Данное подмножество состоит из четырех элементов, поэтому можно анализировать произведение его элементов: 2 * 3 * 4 * 5 = 120. Решение найдено.
|
|
0 |
1 |
2 |
3 |
4 |
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
Бинарное число BinaryNumber |
1 |
1 |
1 |
1 |
1 |
|
Подмножество Group |
1 |
2 |
3 |
4 |
5 |
Ниже приведена программа, реализующая данный подход.
// Необходимо найти все четверки элементов данного одномерного
// мacсива натуральных чисел, произведение которых равно 120
// Задача решается полным перебором всех подмножеств исходного массива.
// Полный перебор реализуется через бинарное число,
// количество разрядов которого равно количеству элементов массива
#include "stdafx.h"
#include <conio.h>
#include <math.h>
#define MAX_SIZE 100 // максимальная длина исходного массива
#define GROUP_SIZE 4 // размерность подмножества
#define MULT 120 // произведение элементов подмножества
// Увеличить бинарное число на единицу
void IncBinaryNumber(int *BinaryNumber, int NumberWidth);
// Применить маску к массиву
void ApplyMask(int *Mass, int MassSize, int *Mask,
int *ResultMass, int *ResultMassSize);
// Рассчитать произведение элементов массива
int MultMassElements(int *Mass, int MassSize);
// Заполнить массив значением Value
void FillMass(int *Mass, int MassSize, int Value);
// Ввести массив
void InputMass(int *Mass, int MassSize);
// Распечатать массив
void PrintMass(int *Mass, int MassSize);
int _tmain(int argc, _TCHAR* argv[])
{
int Mass[MAX_SIZE]; // исходный массив
int MassSize; // фактический размер массива
int BinaryNumber[MAX_SIZE]; // бинарное число, каждый разряд
// которого указывает, что
// соответсвующий элемент массива Mass
// входит в подмножество элементов
int Group[MAX_SIZE]; // подмножество массива Mass
int CurGroupSize; // размер текущего подмножества
int i;
// Вводим размерность исходного массива
printf("Input mass size: ");
scanf("%d", &MassSize);
// Вводим исходный массив
InputMass(Mass, MassSize);
// Ищем подмножества из GROUP_SIZE элементов, произведение которых
// равно MULT, и распечатываем их
// Изначально ни один элемент массива Mass не входит в подмножество элементов -
// обнуляем бинарное число
FillMass(BinaryNumber, MAX_SIZE, 0);
// Формируем подмножества из всех возможных сочетаний элементов
// массива Mass и печатаем те из них, размер которых равен GROUP_SIZE, а
// прозведение элементов равно MULT
for(i= 0; i < pow((float)2, (float)MassSize); i++)
{
// Формируем очередное подмножество массива Mass
IncBinaryNumber(BinaryNumber, MassSize);
ApplyMask(Mass, MassSize, BinaryNumber, Group, &CurGroupSize);
// Выводим подмножество, если его размер равен GROUP_SIZE, а
// произведение его элементов равно MULT
if(CurGroupSize == GROUP_SIZE)
{
if(MultMassElements(Group, GROUP_SIZE) == MULT)
{
printf("\n");
PrintMass(Group, GROUP_SIZE);
}
}
}
_getch();
return 0;
}
// Увеличить бинарное число на единицу
//
// BinaryNumber - бинарное число большой размерности
// NumberWidth - размерность числа
//
void IncBinaryNumber(int *BinaryNumber, int NumberWidth)
{
int LowDigitOver; // переполнение младшего разряда (0 или 1)
int i;
LowDigitOver= 1; // фиктивное переполнение несуществующего младшего разряда
for(i= 0; i < NumberWidth; i++)
{
// Увеличиваем на единицу i-й разряд бинарного числа, если
// переполнился младший - (i-1)-й разряд
BinaryNumber[i]+= LowDigitOver;
// Определяем, переполнился ли разряд
if(BinaryNumber[i] > 1)
{
BinaryNumber[i]= 0;
LowDigitOver= 1;
}
else
{
LowDigitOver= 0;
}
}
}
// Применить маску к массиву: из массива Mass выбираются элементы,
// которые в маске Mask помечены единицами
//
// Mass - исходный массив, к которому применяется маска
// MassSize - размер исходного массива
// Mask - маска: 1 - элемент Mass попадает в конечный массив, 0 - нет
// ResultMass - результирующий массив
// ResultMassSize - размер результирующего массива
//
void ApplyMask(int *Mass, int MassSize, int *Mask, int *ResultMass, int *ResultMassSize)
{
int i;
*ResultMassSize= 0;
for(i= 0; i < MassSize; i++)
{
if(Mask[i] == 1) // в маске присутствует 1
{
// Записываем в результирующий массив элемент исходного массива
ResultMass[*ResultMassSize]= Mass[i];
// Увеличиваем размер результирующего массива
(*ResultMassSize)++;
}
}
}
// Рассчитать произведение элементов массива
//
// Mass - массив
// MassSize - размер массива
//
// Функция по умолчанию возращает единицу
//
int MultMassElements(int *Mass, int MassSize)
{
int Result;
int i;
Result= 1;
for(i= 0; i < MassSize; i++)
{ Result*= Mass[i]; }
return Result;
}
// Заполнить массив значением Value
//
// Mass - массив
// MassSize - размер массива
// Value - значение для заполнения
//
void FillMass(int *Mass, int MassSize, int Value)
{
int i;
for(i= 0; i < MassSize; i++)
{ Mass[i]= Value; }
}
// Ввести массив
//
// Mass - массив
// MassSize - размер массива
//
void InputMass(int *Mass, int MassSize)
{
int i;
for(i= 0; i < MassSize; i++)
{
printf("Mass[%02d]= ", i);
scanf("%d", &Mass[i]);
}
}
// Распечатать массив
//
// Mass - массив
// MassSize - размер массива
//
void PrintMass(int *Mass, int MassSize)
{
int i;
for(i= 0; i < MassSize; i++)
{ printf(" %2d ", Mass[i]); }
}
Рассмотренный подход отличается относительной алгоритмической простотой и универсальностью. Однако в задачах большой размерности он малоэффективен, т.к. порождает очень большое количество потенциальных решений = 2N. Кроме того, данный метод не применим, если невозможно (или сложно) сразу построить конечное потенциальное решение и проверить его на соответствие условию задачи. Примером такой задачи может быть следующая задача.
Формулировка задания:
Напишите программу, реализующую передвижение коня по всем 64 клеткам доски так, чтобы он прошел максимальное расстояние, не пересекая собственных путей.
|
Окончание занятия №28 (лекция) |
Реализация сокращенного перебора с учетом ограничений, содержащихся в условии задачи
Количество потенциальных решений можно сократить, если генерировать их с учетом ограничений, заложенных в условии задачи. Например, в решаемой задаче можно генерировать не все подмножества массива, а только те, которые состоят из четырех элементов (четверки). Для генерации четверок на основе заданного массива Mass используются следующие правила:
1) Первый элемент подмножества выбирается среди элементов Mass[0]Mass[N-1-3], пусть его индекс i.
2) Второй элемент подмножества выбирается среди элементов Mass[i+1]Mass[N-1-2], пусть его индекс j.
3) Третий элемент подмножества выбирается среди элементов Mass[j+1]Mass[N-1-1], пусть его индекс k.
4) Четвертый элемент подмножества выбирается среди элементов Mass[k+1]Mass[N-1], пусть его индекс m.
Ниже приведена трасса поиска подмножеств для массива размерности N=5.
|
|
0 |
1 |
2 |
3 |
4 |
|
|
Исходный массив Mass |
1 |
2 |
3 |
4 |
5 |
|
|
Подмножество Group [0][1][2][3] |
1 |
2 |
3 |
4 |
|
1*2*3*4 = 24 |
|
Подмножество Group [0][1][2][4] |
1 |
2 |
3 |
|
5 |
1*2*3*5 = 30 |
|
Подмножество Group [0][1][3][4] |
1 |
2 |
|
4 |
5 |
1*2*4*5 = 40 |
|
Подмножество Group [0][2][3][4] |
1 |
|
3 |
4 |
5 |
1*3*4*5 = 60 |
|
Подмножество Group [1][2][3][4] |
|
2 |
3 |
4 |
5 |
2*3*4*5 = 120 |
Ниже приведена программа, реализующая данный подход.
// Необходимо найти все четверки элементов данного одномерного
// мacсива натуральных чисел, произведение которых равно 120
// Задача решается полным перебором всех четверок исходного массива.
#include "stdafx.h"
#include <conio.h>
#define MAX_SIZE 100 // максимальная длина исходного массива
#define GROUP_SIZE 4 // размерность подмножества
#define MULT 120 // произведение элементов подмножества
// Рассчитать произведение элементов массива
int MultMassElements(int *Mass, int MassSize);
// Заполнить массив значением Value
void FillMass(int *Mass, int MassSize, int Value);
// Ввести массив
void InputMass(int *Mass, int MassSize);
// Распечатать массив
void PrintMass(int *Mass, int MassSize);
int _tmain(int argc, _TCHAR* argv[])
{
int Mass[MAX_SIZE]; // исходный массив
int MassSize; // фактический размер массива
int Group[GROUP_SIZE]; // подмножество массива Mass
int i, j, k, m; // индексы элементов исходного массива,
// составляющих четверки
// Вводим размерность исходного массива
printf("Input mass size: ");
scanf("%d", &MassSize);
// Вводим исходный массив
InputMass(Mass, MassSize);
// Изначально подмножество пустое
FillMass(Group, GROUP_SIZE, 0);
// Ищем подмножества, размер которых равен GROUP_SIZE, а произведение
// элементов равно MULT, и распечатываем их
for(i= 0; i <= (MassSize - 1) - (GROUP_SIZE - 1); i++) // выбор индекса
// первого эл-та подмн-ва
{
Group[0]= Mass[i];
for(j= i+1; j <= (MassSize - 1) - (GROUP_SIZE - 2); j++) // выбор индекса
// второго эл-та подмн-ва
{
Group[1]= Mass[j];
for(k= j+1; k <= (MassSize - 1) - (GROUP_SIZE - 3); k++) // выбор индекса
// третьего эл-та подмн-ва
{
Group[2]= Mass[k];
for(m= k+1; m <= (MassSize - 1) - (GROUP_SIZE - 4); m++) // выбор индекса
// четвертого эл-та подмн-ва
{
Group[3]= Mass[m];
// Распечат. подмнож-во, если произведение его элементов равно MULT
if(MultMassElements(Group, GROUP_SIZE) == MULT)
{
printf("\n");
PrintMass(Group, GROUP_SIZE);
}
}
}
}
}
_getch();
return 0;
}
// Рассчитать произведение элементов массива
//
// Mass - массив
// MassSize - размер массива
//
// Функция по умолчанию возращает единицу
//
int MultMassElements(int *Mass, int MassSize)
{
int Result;
int i;
Result= 1;
for(i= 0; i < MassSize; i++)
{ Result*= Mass[i]; }
return Result;
}
// Заполнить массив значением Value
//
// Mass - массив
// MassSize - размер массива
// Value - значение для заполнения
//
void FillMass(int *Mass, int MassSize, int Value)
{
int i;
for(i= 0; i < MassSize; i++)
{ Mass[i]= Value; }
}
// Ввести массив
//
// Mass - массив
// MassSize - размер массива
//
void InputMass(int *Mass, int MassSize)
{
int i;
for(i= 0; i < MassSize; i++)
{
printf("Mass[%02d]= ", i);
scanf("%d", &Mass[i]);
}
}
// Распечатать массив
//
// Mass - массив
// MassSize - размер массива
//
void PrintMass(int *Mass, int MassSize)
{
int i;
for(i= 0; i < MassSize; i++)
{ printf(" %2d ", Mass[i]); }
}
Рассмотренный подход обладает наибольшей эффективностью, но имеет существенный недостаток – не всегда заранее известна последовательность шагов, приводящая к получению потенциального решения, или таких шагов очень много. Например, если в решаемой задаче необходимо было найти все подмножества, произведение элементов которых давало бы 120, то данный подход был бы не применим, т.к. невозможно реализовать заранее неизвестное количество вложенных циклов.
Реализация сокращенного перебора – построение дерева решений
Если последовательность шагов, приводящая к получению потенциального решения, заранее не известна, то потенциальное решение строится пошагово. Сначала рассматривается исходная ситуация (ни один элемент массива не входит в подмножество), затем выполняется одно из действий, приближающее нас к получению потенциального решения (выбор из массива очередного элемента множества), в результате получаем промежуточное потенциальное решение. Через некоторое количество шагов будет получено конечное потенциальное решение (четверка элементов). Если полученное решение нас не удовлетворяет (или нужно найти все), то происходит шаг назад к предыдущему промежуточному потенциальному решению и выполняется альтернативное действие, приводящее к новому потенциальному решению. Если все альтернативные действия исчерпаны, то возврат происходит еще на шаг назад и процедура повторяется. Этот процесс построения потенциальных решений можно представить в виде дерева решений.

При построении дерева решений использовались следующие правила:
1) Исходная ситуация – пустое подмножество элементов массива;
2) Промежуточное потенциальное решение получается из предыдущего выбором из массива очередного элемента подмножества. При этом очередной элемент подмножества должен выбираться из элементов Mass[LastIndex+1]Mass[(N-1)-(4-n)], где LastIndex – индекс элемента исходного массива, который последним попал в подмножество, N – размер исходного массива, n – кол-во элементов, которое уже попало в подмножество.
3) Конечное потенциальное решение – подмножество, состоящее из четырех элементов.
Ниже приведена программа, реализующая построение дерева решений. Необходимо отметить, что для построения дерева решений использовалась рекурсия.
// Необходимо найти все четверки элементов данного одномерного
// мacсива натуральных чисел, произведение которых равно 120
// Задача решается полным перебором всех четверок исходного массива.
// Полный перебор реализуется построением дерева возможных решений.
// Дерево строится с исползьзованием рекурсии
#include "stdafx.h"
#include <conio.h>
#define MAX_SIZE 100 // максимальная длина исходного массива
#define GROUP_SIZE 4 // размерность подмножества
#define MULT 120 // произведение элементов подмножества
// Поиск подмножеств элементов массива Mass, размер которых равен GroupSize и
// произведение которых равно Mult, и его печать
void SelectGroup(int *Mass, int MassSize, int *Group, int GroupSize, int Mult,
int CurGroupSize, int LastIndex);
// Рассчитать произведение элементов массива
int MultMassElements(int *Mass, int MassSize);
// Заполнить массив значением Value
void FillMass(int *Mass, int MassSize, int Value);
// Ввести массив
void InputMass(int *Mass, int MassSize);
// Распечатать массив
void PrintMass(int *Mass, int MassSize);
int _tmain(int argc, _TCHAR* argv[])
{
int Mass[MAX_SIZE]; // исходный массив
int MassSize; // фактический размер массива
int Group[GROUP_SIZE]; // подмножество массива Mass
// Вводим размерность исходного массива
printf("Input mass size: ");
scanf("%d", &MassSize);
// Вводим исходный массив
InputMass(Mass, MassSize);
// Изначально подмножество пустое
FillMass(Group, GROUP_SIZE, 0);
// Ищем подмножества из GROUP_SIZE элементов, произведение которых
// равно MULT, и распечатываем их
SelectGroup(Mass, MassSize, Group, GROUP_SIZE, MULT, 0, -1);
_getch();
return 0;
}
// Поиск подмножеств элементов массива Mass, размер которых равен GroupSize и
// произведение которых равно Mult, и его печать
// Mass - исходный массив
// MassSize - фактический размер исходного массива
// Group - подмножество исходного массива
// GroupSize - требуемый размер подмножества
// Mult - требуемое произведение элементов подмножества
// CurGroupSize - текущее кол-во элементов, входящее в подмножество
// LastIndex - индекс элемента исходного массива, который последним попал в
// подмножнство
void SelectGroup(int *Mass, int MassSize, int *Group, int GroupSize, int Mult,
int CurGroupSize, int LastIndex)
{
int BeginIndex, EndIndex; // интервал элементов массива Mass, в котором
// ищем очередной элемент подмножества
int i;
if(CurGroupSize == GroupSize) // нашли все элементы подмножества
{
// Распечат. подмнож-во, если произведение его элементов равно Mult
if(MultMassElements(Group, GroupSize) == Mult)
{
printf("\n");
PrintMass(Group, GroupSize);
}
}
else // нашли еще не все элементы подмножества
{
CurGroupSize++; // ищем очередной элемент подмножества
// Определяем интервал поиска очередного элемента
// подмножества, учитывая следующее: очередной элемент лежит
// правее предыдущего элемента и левее последующих элементов,
// составляющих конец массива
if(CurGroupSize == 1)
{ BeginIndex= 0; }
else
{ BeginIndex= LastIndex + 1; }
EndIndex= MassSize-1-(GroupSize-CurGroupSize);
// Анализируем все возможные подмножества, включающие в себя
// очередной элемент, взятый из интервала [BeginIndex, EndIndex]
for(i= BeginIndex; i <= EndIndex; i++)
{
Group[CurGroupSize-1]= Mass[i]; // рассматриваем i-й элемент Mass в качестве
// очередного элемента подмножества
SelectGroup(Mass, MassSize, Group, GroupSize, Mult, CurGroupSize, i);
Group[CurGroupSize-1]= 0; // отменяем i-й элемент Mass в качестве
// очередного элемента подмножества
}
}
}
// Рассчитать произведение элементов массива
//
// Mass - массив
// MassSize - размер массива
//
// Функция по умолчанию возращает единицу
//
int MultMassElements(int *Mass, int MassSize)
{
int Result;
int i;
Result= 1;
for(i= 0; i < MassSize; i++)
{ Result*= Mass[i]; }
return Result;
}
// Заполнить массив значением Value
//
// Mass - массив
// MassSize - размер массива
// Value - значение для заполнения
//
void FillMass(int *Mass, int MassSize, int Value)
{
int i;
for(i= 0; i < MassSize; i++)
{ Mass[i]= Value; }
}
// Ввести массив
//
// Mass - массив
// MassSize - размер массива
//
void InputMass(int *Mass, int MassSize)
{
int i;
for(i= 0; i < MassSize; i++)
{
printf("Mass[%02d]= ", i);
scanf("%d", &Mass[i]);
}
}
// Распечатать массив
//
// Mass - массив
// MassSize - размер массива
//
void PrintMass(int *Mass, int MassSize)
{
int i;
for(i= 0; i < MassSize; i++)
{ printf(" %2d ", Mass[i]); }
}
В данном случае дерево реализуется с использованием рекурсии, т.к. в общем случае глубина дерева не известна.
|
Окончание занятия №30 (практика) |
Приложение 1. Базовые алгоритмические структуры
|
Название |
|
СЛЕДОВАНИЕ |
|
Признаки |
|
Разнородные действия, следующие друг за другом. Каждое действие обязательно выполняется. |
|
Порядок декомпозиции |
|
1. Записываются предложения, описывающие последовательно выполняемые действия. 2. Проверяется информационная совместимость действий и рационализируется их порядок, уточняется суть действий. |
|
Словесный алгоритм |
|
N. <Действие> N.1. <Действие 1> N.2. <Действие 2> .................. N.M. <Действие M> |
|
Блок-схема |
|
|
|
Запись на языке Си |
|
// <Действие> <Оператор 1> <Оператор 2> ... <Оператор M> |
|
Пример записи на языке Си |
|
// Вычисление выражения y = cos(s)/(a*x) y = cos(s); y = y/(a*x);
|
|
Название |
|
АЛЬТЕРНАТИВА | |
|
Признаки |
|
Два действия, каждое из которых выполняется при определенном условии. Одно действие выполняется при определенном условии или не выполняется вообще. | |
|
Порядок декомпозиции |
|
1. Записываются альтернативные действия. 2. Записываются условия выполнения альтернативных действий. 3. Осуществляется проверка информационной согласованности входа и выхода каждого из действия и их условий выполнения. | |
|
Словесный алгоритм |
|
N. <Действие> Если <Условие> N.1. <Действие 1> Иначе N.2. <Действие 2> |
N. <Действие> Если <Условие> N.1. <Действие 1>
|
|
Блок-схема |
|
|
|
|
Запись на языке Си |
|
// <Действие> if(<Условие>) { <Оператор 1> } else { <Оператор 2> } |
// <Действие> if(<Условие>) { <Оператор 1> }
|
|
Пример записи на языке Си |
|
// Вычисление y= |x| if(x < 0) { y= -x; } else { y= x; } |
// Ограничиваем число // максимальным значением if(x > max) x= max; |
|
Название |
|
ВЫБОР | ||
|
Признаки |
|
АЛЬТЕРНАТИВА с более чем двумя альтернативными действиями. | ||
|
Порядок декомпозиции |
|
Аналогично структуре АЛЬТЕРНАТИВА. | ||
|
Словесный алгоритм |
|
N. <Действие> Если <Условие 1> N.1. <Действие 1> Если <Условие 2> N.2. <Действие 2> ..................... Если <Условие M> N.M. <Действие M> Иначе N.M+1. <Действие M+1> | ||
|
Блок-схема |
|
| ||
|
Запись на языке Си |
|
// <Действие> if(<Условие 1>) { <Оператор 1> } if(<Условие 2>) { <Оператор 2> } .................. if(<Условие M>) { <Оператор M> } |
// <Действие> if(<Условие 1>) { <Оператор 1> } else if(<Условие 2>) { <Оператор 2> } .................. else if(<Условие M>) { <Оператор M> } else { <Оператор M+1> } |
// <Действие> switch(<Выражение>) { case <Константа 1>: <Оператор 1> break;
case <Константа 2>: <Оператор 2> break; .................. case <Константа M>: <Оператор M> break;
default: <Оператор M+1> break; } |
|
Пример записи на языке Си |
|
// Вычисление y= sign(x) if(x < 0) { y= -1; } if(x == 0) { y= 0; } if(x > 0) { y= 1; } | ||
|
// Вычисление y= sign(x) if (x < 0) { y= -1; } else if(x == 0) { y= 0; } else if(x > 0) { y= 1; } | ||||
|
// Преобразование числа из десятичной (Number) // в римскую (RomanNumber) систему исчисления switch(Number) { case 1: strcpy(RomanNumber, “I”); break;
case 2: strcpy(RomanNumber, “II”); break;
case 3: strcpy(RomanNumber, “III”); break;
case 4: strcpy(RomanNumber, “IV”); break;
case 5: strcpy(RomanNumber, “V”); break;
default: strcpy(RomanNumber, “”); } | ||||
|
Название |
|
ЦИКЛ С ПРЕДУСЛОВИЕМ |
|
Признаки |
|
Многократное выполняемое действие (но обязательно конечное число раз). Переменное количество АЛЬТЕРНАТИВ. Любая мысль о возврате “назад” чтобы повторить какие-то действия. Использование выражений “и т.д.”, “и т.п.”. Действие может не выполняться ни разу. |
|
Порядок декомпозиции |
|
1. Записывается многократно выполняемое действие. 2. Определяется условие продолжения цикла. 3. Записывается действие, определяющее окончание повторения процесса. 4. Записывается действие, определяющее подготовку повторяющихся действий. |
|
Словесный алгоритм |
|
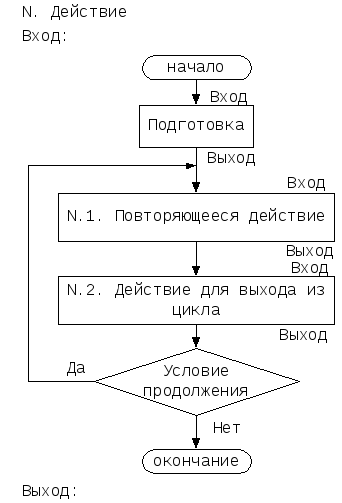
N. <Действие> Подготовка: <Подготовка> Пока <Условие продолжения> N.1. <Повторяющееся действие> N.2. <Действие для выхода из цикла> |
|
Блок-схема |
|
|
|
Запись на языке Си |
|
// <Действие> <Оператор 1> // <Подготовка> while(<Условие>) // <Условие продолжения> { <Оператор 2> // <Повторяющееся действие> <Оператор 3> // <Действие для выхода из цикла> } |
|
Пример записи на языке Си |
|
// Подсчитываем количество символов в строке Text Count = 0; while(Text[Count]!=‘\0’) { Count++; } |
|
Название |
|
ЦИКЛ С ПОСТУСЛОВИЕМ |
|
Признаки |
|
Аналогично структуре ЦИКЛ С ПРЕДУСЛОВИЕМ, но действие должно выполниться хотя бы один раз. |
|
Порядок декомпозиции |
|
Аналогично структуре ЦИКЛ С ПРЕДУСЛОВИЕМ. |
|
Словесный алгоритм |
|
N. <Действие> Подготовка: <Подготовка> Делать N.1. <Повторяющееся действие> N.2. <Действие для выхода из цикла> Пока <Условие продолжения> |
|
Блок-схема |
|
|
|
Запись на языке Си |
|
// <Действие> <Оператор 1> // <Подготовка> do { <Оператор 2> // <Повторяющееся действие> <Оператор 3> // <Действие для выхода из цикла> } while(<Условие>); // <Условие продолжения> |
|
Пример записи на языке Си |
|
// Запрашиваем у пользователя число от 0 до 10 do { scanf(“%d”, &Number); } while((Number < 0) || (Number > 10)); |
|
Название |
|
ПАРАМЕТРИЧЕСКИЙ ЦИКЛ |
|
Признаки |
|
Заданное число повторений. Заданный интервал значений. |
|
Порядок декомпозиции |
|
Аналогично структуре ЦИКЛ С ПРЕДУСЛОВИЕМ. |
|
Словесный алгоритм |
|
N. <Действие> Подготовка: <Подготовка> Выполнять K раз N.1. <Повторяющееся действие> |
|
N. <Действие> Подготовка: <Подготовка> Выполнять при R i S с шагом T N.1. <Повторяющееся действие> | ||
|
Блок-схема |
|
|
|
| ||
|
Запись на языке Си |
|
// <Действие> <Оператор 1> // <Подготовка> for(i= 1; i<= K; i++) { <Оператор 2> // <Повторяющееся действие> } |
|
// <Действие> <Оператор 1> // <Подготовка> for(i= S; i<= R; i= i+T) { <Оператор 2> // <Повторяющееся действие> } | ||
|
Пример записи на языке Си |
|
// Вычисление y = xn без использования библиотечн. функции y = 1; for(i= 1; i <= n; i++) { y= y*x; } |
|
// Вычисление y = n! y = 1; for(i= 1; i <= n; i++) { y= y*i; } |