24

Программирование на языках высокого уровня. Алгоритмические языки

Лекции

Содержание

Разработка (проектирование) одномодульных программ

Написание хороших программ

требует ума, вкуса и терпения.

Б. Страуструп

Критерии качества программы и ее разработки

Критерии качества программы с точки зрения пользователя:

– функциональная полнота:

– программа должна решать весь класс задач, для которых она предназначена;

– должны учитываться все возможные ситуации, возникающие при решении задачи;

– высокая надежность: программа должна правильно работать при всех входных данных, даже если они не соответствуют условию задачи;

– приемлемая стоимость: стоимость во многом определяется сроками разработки программы – чем меньше сроки разработки, тем меньше стоимость, и наоборот;

– простота и логичность работы в программе: многие программы просто не используются, если имеются программы-конкуренты с более простым и интуитивно понятным интерфейсом;

– приемлемые требования к аппаратным ресурсам: на сегодняшний день эта проблема успешно решается покупкой нового компьютера, тем более, что некоторые программы стоят дороже, чем компьютер;

– приемлемые сроки разработки: обычно пользователь не готов ждать несколько лет, пока программист будет разрабатывать программу. Сроки разработки во многом зависят от сложности решаемой задачи, но они могут быть сокращены за счет правильного подхода к решению задачи, а также при совместной разработке программы группой программистов.

Критерии качества программы и ее разработки с точки зрения программиста:

– простота и ясность решения задачи: одна и та же задача может решаться различными способами, но в большинстве случаев лучшим решением считается наиболее простое (исключением из этого правила является ситуация, когда требуется максимальная скорость выполнения и/или минимальный объем расходуемой памяти);

– хорошо читаемый код: самая простая программа будет непонятна, если она неверно отформатирована и не имеет комментариев;

– простота отладки: в среднем на отладку затрачивается до 60% времени от общего процесса создания программы, поэтому эффективность отладки значительно влияет на сроки разработки программы и ее стоимость. Простота отладки обеспечивается простотой и ясностью решения задачи и хорошо читаемым кодом программы;

– возможность и простота модификации: если программа «живет» долго, то она претерпевает множество изменений. Простота внесения изменений в программу определяется теми же критериями, что эффективность отладки. Кроме того, программу проще модифицировать, если она состоит из отдельных, почти независимых «частей» (функций и/или классов), которые можно изменять независимо друг от друга;

– возможность разработки программы группой программистов: если один программист может создать программу за 6 месяцев, то 6 программистов туже программу создадут за N месяцев, где N > 0. Значение N во многом определяется эффективностью взаимодействия программистов и в худшем случае может составить более 6 месяцев. Отчасти проблему взаимодействия программистов можно разрешить, если программа будет иметь простое и понятное решение и будет хорошо документирована;

– приемлемые сроки и затраты на разработку: сроки и затраты определяются вышеперечисленными критериями.

Исходя из вышесказанного, «качественной» программой можно считать программу, которая обладает «внутренней» простотой и хорошо читаема. Умение создавать такие программы является важнейшим навыком программиста.

Пример «некачественной» программы. Данная программа полностью работоспособна, но понять, что она делает, а главное как – практически невозможно.

#include "stdafx.h"

int _tmain(int argc, _TCHAR* argv[])

{ float a1, a2; int a3= 0;

do { printf("Введите координату X ");

scanf("%f", &a1);

printf("\nВведите координату Y "); scanf("%f", &a2);

if(a1 > 0){ if(a2==0) printf("\nТочка попала на полуось +X");

else if(a2>0)

printf("\nТочка попала в I квадрант");

else printf("\nТочка попала в IV квадрант");

}

else {

if(a1 < 0)

if(a2 >0)printf("\nТочка попала во II квадрант");

else if(a2==0)

printf("\nТочка попала на полуось -X"); else printf("\nТочка попала в III квадрант");

else if(a2>0) printf("\nТочка попала на полуось +Y");

else if(a2<0) {printf("\nТочка попала на полуось -Y");}

else printf("\nТочка попала в начало координат");

}

printf("\n\nБудете еще работать (1 - Да, 0 - Нет) ? ");

scanf("%d", &a3);

} while(a3 == 1);

return 0;}

Пример «качественной» программы. Эта программа решает туже задачу, что и предыдущая программа, но имеет «правильное» решение и форматирование.

#include "stdafx.h"

// Определение положения точек на координатной плоскости

int _tmain(int argc, _TCHAR* argv[])

{

float x, y; // координаты точки

int IsContinue= 0; // признак продолжения работы (1 - да, 0 - нет)

// Определение местонахождения точек

do

{

// Ввод координат для очередной точки

printf("Введите координату X ");

scanf("%f", &x);

printf("\nВведите координату Y ");

scanf("%f", &y);

if((x > 0)&&(y == 0)) // точка попадает на полуось +X

{ printf("\nТочка попала на полуось +X"); }

if((x > 0)&&(y > 0)) // точка попадает в I квадрант

{ printf("\nТочка попала в I квадрант"); }

if((x == 0)&&(y > 0)) // точка попадает на полуось +Y

{ printf("\nТочка попала на полуось +Y"); }

if((x < 0)&&(y > 0)) // точка попадает во II квадрант

{ printf("\nТочка попала во II квадрант"); }

if((x < 0)&&(y == 0)) // точка попадает на полуось -X

{ printf("\nТочка попала на полуось -X"); }

if((x < 0)&&(y < 0)) // точка попадает в III квадрант

{ printf("\nТочка попала в III квадрант"); }

if((x == 0)&&(y < 0)) // точка попадает на полуось -Y

{ printf("\nТочка попала на полуось -Y"); }

if((x > 0)&&(y < 0)) // точка попадает в IV квадрант

{ printf("\nТочка попала в IV квадрант"); }

if((x == 0)&&(y == 0)) // точка пападает в цент координат

{ printf("\nТочка попала в начало координат"); }

// Определение возможности продолжения работы

printf("\n\nБудете еще работать (1 - Да, 0 - Нет) ? ");

scanf("%d", &IsContinue);

} while(IsContinue == 1);

return 0;

}

Если вы еще не догадались, что делает программа, то скажу, что программа определяет положение точки на координатной плоскости.

Окончание занятия №1 (лекция)

Понятие алгоритма. Свойства алгоритма

«Внутренняя» простота или сложность программы определяется ее алгоритмом.

Алгоритм – это предписание в виде конечной последовательности дискретных шагов, которое задает процесс преобразования исходной информации в результат.

Не любая последовательность действий считается алгоритмом. Алгоритм должен обладать массовостью, дискретностью, определенностью и результативностью.

Массовость – применимость алгоритма ко всем задачам рассматриваемого класса при любых исходных данных.

Дискретность – свойство алгоритма, означающее, что процесс преобразования исходных данных в результат должен делиться на отдельные законченные элементарные шаги. Каждый такой шаг должен использовать данные, полученные на предыдущем шаге, и выдавать промежуточные результаты, которые будут использованы последующими шагами.

Определенность – свойство алгоритма, состоящее в том, что каждое входящее в него действие должно быть строго определено и не допускать различных толкований. Так же строго должен быть определен и порядок выполнения отдельных действий.

Результативность – алгоритм всегда должен завершаться за конечное число шагов, приводя к определенному результату.

Алгоритмы существуют не только в программировании, они используются нами и в повседневной жизни. Рецепт приготовления пирога и инструкция по настройке телевизора являются примерами алгоритмов из повседневной жизни.

Для составления «хорошего» алгоритма программы рекомендуется следующая последовательность шагов:

– постановка задачи.

– разработка тестовых примеров.

– разработка структуры данных.

– составление алгоритма.

– тестирование алгоритма.

– кодирование алгоритма.

Постановка задачи

На этом этапе программист определяет, что должна делать будущая программа. В результате должна быть получена внешняя спецификация программы, включающая в себя выход, вход и главную функцию программы, а также схему диалога пользователя с программой.

В разделе «выходные данные» должны быть отражены результаты работы программы (список «расчетных» величин), способ их представления (вывод на экран или в файл) и ограничения на получаемые результаты (диапазоны получаемых значений, их тип).

В разделе «входные данные» перечисляются исходные данные, необходимые для решения задачи. Описание данного раздела выполняется аналогично разделу «выходные данные».

В разделе «главная функция» указывается действие, которое выполняет программа для преобразования входных данных в выходные. Главная функция программы должна представляться одним предложением, содержащим либо глагол, либо отглагольное существительное. Кроме того, в главной функции программы должны быть отражены ограничения на решения задачи, например, «упорядочивание массива по возрастанию методом пузырька».

Последним разделом внешней спецификации программы является «схема диалога» пользователя с программой. В нем приводится пример диалога в том виде, в котором он будет выглядеть на экране.

Внешнюю спецификацию можно считать хорошей, если из нее понятно, чтодолжна делать программа, и нет неоднозначностей в ее толковании.

Внешняя спецификация программы, рассчитывающей корни квадратного уравнения.

Выходные данные: действительные корни квадратного уравнения (вещественные числа) и сообщения (см. диалог). Варианты сообщений: «Корни квадратного уравнения x1= ... и x2= ...», «Корень квадратного уравнения x= ...», «Нет действительных корней квадратного уравнения», «Корень линейного уравнения x= ...», «x – любое число», «Уравнение задано неверно». Значения по модулю корней квадратного уравнения не могут превышать 32000.

Входные данные: коэффициенты квадратного уравнения a, b, c (вещественные числа) (см. диалог). Значения по модулю коэффициентов квадратного уравнения не могут превышать 32000.

Главная функция: расчет корней квадратного уравнения .

Диалог:

Расчет корней квадратного уравнения.

Введите коэффициент a = 1

Введите коэффициент b = -11

Введите коэффициент c = 30

Корни квадратного уравнения x1= 6 и x2= 5

Полученная внешняя спецификация программы имеет важную роль не только для программиста, но и для будущего пользователя (заказчика) программы: она позволяем удостовериться ему в том, что учтены все его пожелания и потребности. При наличии разногласий между пользователем и программистом вырабатывается взаимоприемлемый вариант внешней спецификации.

Разработка тестовых примеров

Зная, что должна делать программа, программист должен придумать (или позаимствовать из книг, Internet, у друзей и т.д.) идею решения задачи. Генерация идеи решения задачи сродни сочинению стихов или доказательству теорем, а потому трудно дать какие-либо конкретные рекомендации – многое зависит от опыта и способностей программиста. Однако создаваемая идея должна учитывать возможности компьютера, а точнее языка программирования.

После генерации идеи, ее необходимо проверить (протестировать) на конкретных примерах (тестах), придать ей реализацию в виде конкретных шагов. При этом возможны три случая:

– идея решения «работает» на всех примерах, следовательно, мы находимся на правильном пути;

– идея решения не позволяет получить правильные результаты ни на одном из тестов, следовательно, необходимо придумать новую идею или модифицировать существующую;

– идея решения на некоторых тестах дает неверные результаты, следовательно, для этих случаев нужно придумать новую идею решения, а, возможно, не одну.

Замечание. В сложных случаях идея решения задачи изначально не видна и тогда решение конкретного примера позволяет «натолкнуться» на идею.

Окончание занятия №2 (лекция)

Важным вопросом является количество примеров (тестов), на которых необходимо осуществлять проверку идеи решения. Ответ на этот вопрос таков – количество тестов должно быть не менее количества вариантов решения задачи. Иногда в набор тестов включают дополнительные примеры, решение которых сводится к уже существующим, но это не очевидно.

Составление набора тестов является нетривиальной задачей (как и генерация идеи решения), а потому трудно дать какие-либо конкретные рекомендации. В общем случае следует начинать решать задачу с наиболее очевидного случая, а затем, анализируя его, пытаться придумывать контрпримеры.

Теперь перейдем к тому, как тестируется идея решения задачи. Тест должен включать в себя следующие разделы:

– исходные данные: представляются набором переменных и их значений;

– действия, приводящие к решению задачи, и результаты этих действий. Каждое действие записываются в виде предложения на русском языке или математического выражения. В действиях обязательно должны быть указаны переменные, над которыми эти действия выполняются. Результаты действий представляются значениями переменных;

– обобщение – это набор действий без конкретных значений переменных;

– условие применимости – условие, определяющее случаи, когда данное обобщение применимо для решения задачи.

Замечание. В сложных задачах рекомендуется использовать принцип декомпозиции: сначала задача разбивается на небольшое количество подзадач, а затем каждая из подзадач тестируется отдельно. Так продолжается до тех пор, пока задача не будет сведена к элементарным действиям.

Тестовые примеры для программы, рассчитывающей корни квадратного уравнения.

Тест №1: a= 1, b= -11, c= 30

Рассчитать дискриминант D= b*b-4*a*c= 121-120= 1

Рассчитать корни уравнения:

x1= (-b + D)/(2*a)= (11+1)/2= 6, x2= (-b - D)/(2*a)= (11-1)/2= 5

Печать “Корни квадратного уравнения x1= 6 и x2= 5”

Обобщение:

Рассчитать дискриминант D= b*b-4*a*c

Рассчитать корни уравнения:

x1= (-b + D)/(2*a), x2= (-b - D)/2*a

Печать “Корни квадратного уравнения x1= <x1> и x2= <x2>”

Условие применимости: (a  0) и (D > 0)

Тест №2: a= 1, b= -4, c= 4

Рассчитать дискриминант D= b*b-4*a*c= 16-16= 0

Рассчитать корень уравнения: x= -b/(2*a)= 4/2= 2

Печать “Корень квадратного уравнения x= 2”

Обобщение:

Рассчитать дискриминант D= b*b-4*a*c

Рассчитать корень уравнения: x= -b/(2*a)

Печать “Корень квадратного уравнения x= <x>”

Условие применимости: (a  0) и (D = 0)

Тест №3: a= 1, b= -2, c= 5

Рассчитать дискриминант D= b*b-4*a*c= 4-20= -16

Печать “Нет действительных корней квадратного уравнения”

Обобщение:

Рассчитать дискриминант D= b*b-4*a*c

Печать “Нет действительных корней квадратного уравнения”

Условие применимости: (a  0) и (D < 0)

Тест №4: a= 0, b= -2, c= 5

Рассчитать корень уравнения: x= -c/b= -5/-2= 2.5

Печать “Корень линейного уравнения x= 2.5”

Обобщение:

Рассчитать корень уравнения: x= -c/b

Печать “Корень линейного уравнения x= <x>”

Условие применимости: (a = 0) и (b  0)

Тест №5: a= 0, b= 0, c= 5

Печать “Уравнение задано неверно”

Обобщение:

Печать “Уравнение задано неверно”

Условие применимости: (a = 0) и (b = 0) и (c  0)

Тест №6: a= 0, b= 0, c= 0

Печать “x – любое число”

Обобщение:

Печать “x – любое число”

Условие применимости: (a = 0) и (b = 0) и (c = 0)

Замечание. Тестовые примеры создаются как для правильных, так и неправильных (ошибочных) входных данных, если они могут возникать в процессе работы программы.

Разработка структуры данных

На этом этапе определяется состав переменных, которые будут использоваться в программе. Состав переменных формируется на основе анализа обобщений тестовых примеров. Для каждой переменной указывается ее имя, тип, диапазон возможных значений и описание, отражающее назначение переменной. Вся эта информация может быть представлена в виде таблицы:

Имя	Тип	Описание
…	…	…

При разработке структуры данных необходимо следовать следующим правилам:

1. Имя переменной должно быть мнемоническим, т.е. нести смысл. Лучше всего если имя будет соответствовать предметной области, в которой решается задача. Например: a,b,c,D,x1,x2,x– стандартные обозначения переменных при решении квадратного уравнения;Price,Total– цена и общая сумма при расчете за покупку.

2. Не используйте одну переменную для хранения разной по смыслу информации. Например, использование переменной bдля хранения коэффициента квадратного уравнения и дискриминанта не допускается.

3. Старайтесь указывать тип переменной безотносительно к языку программирования, так как алгоритм должен быть универсальным и не зависеть (по возможности) от языка программирования.

4. Если вы не можете придумать описание переменной, то, скорее всего, либо вы не до конца представляете, как работает алгоритм, либо переменная не нужна вообще. При описании переменной не допускается использование выражений следующего типа: «вспомогательная переменная», «временная переменная» и т.п.

Структура данных для программы, рассчитывающей корни квадратного уравнения.

Имя	Тип	Описание
a, b, c	вещественное число [-32000.00, 32000.00]	Коэффициенты квадратного уравнения
D	вещественное число [4096000000.00, 1024000000.00]	Дискриминант
x, x1, x2	вещественное число [-32000.00, 32000.00]	Корни уравнения

Замечание. Если программист создает свои собственные типы данных, то каждый тип данных описывается в виде отдельной таблицы.

Окончание занятия №3 (практика)

Составление алгоритма

Кто ясно мыслит, тот ясно излагает.

Народная мудрость

Составление алгоритма начинается с представления программы в виде одного «общего» действия (фактически в виде главной функции программы). Затем это действие «разбивается» на ряд более «мелких» действий, каждое из которых подвергается дальнейшему «разбиению» и т.д. Этот процесс декомпозициипродолжается до тех пор, пока программа не будет представлена в виде элементарных действий. Действие считается элементарным, если оно может быть представлено в виде простого оператора языка программирования.

Описанный процесс декомпозиции достаточно жестко регламентирован. Другими словами порядок декомпозиции, количество действий, на которые разбивается «укрупненное» действие, а также порядок выполнения «мелких» действий задаются алгоритмическими структурами. ВПриложении 1представлены шесть базовых алгоритмических структур:СЛЕДОВАНИЕ,АЛЬТЕРНАТИВА,ВЫБОР,ЦИКЛ С ПРЕДУСЛОВИЕМ,ЦИКЛ С ПОСТУСЛОВИЕМ,ПАРАМЕТРИЧЕСКИЙ ЦИКЛ. По сути, алгоритм представляет собой набор вложенных друг в друга алгоритмических структур, а процесс декомпозиции как последовательное решение все более «мелких» задач.

Рассматриваемые алгоритмические структуры обладают одним входом/одним выходом и дискретностью. Наличие одного входа и одного выхода упрощает понимание и отладку алгоритма. Дискретность позволяет рассматривать алгоритм как последовательность задач, которые можно решать независимо. Единственным связующим звеном между этими задачами являются входные и выходные данные, состав которых всегда определяется на более верхнем уровне.

Возможно несколько способов представления алгоритмической структуры, а следовательно и алгоритма: в словесной форме, в виде блок-схем и на языке программирования (см. Приложение 1). Каждый из способов имеет свои достоинства и недостатки. Словесный алгоритм более близок к естественному языку и потому более понятен начинающим программистам. Алгоритм в виде блок-схем более нагляден и содержит информацию о входных и выходных данных, что позволяет легко тестировать алгоритм. Однако этот способ представления значительно отличается от естественного языка. Представление алгоритма на языке программирования собственно является кодом программы (см. ниже). Так как язык программирования сильно отличается от естественного языка, то из текста программы очень трудно понять идею алгоритма. Все указанные способы представления могут быть преобразованы один в другой. Для начинающих программистов следует использовать все три способа представления в следующем порядке: словесный алгоритм, блок-схемы и программа.

Критерием качества алгоритма является его ясность и понятность. Будем придерживаться следующего положения «кто ясно мыслит, тот ясно излагает».

Словесный алгоритм для программы, рассчитывающей корни квадратного уравнения.

Рассчитать корни квадратного уравнения

1. Ввести коэффициенты уравнения a, b, c

2. Рассчитать корни уравнения

2. Рассчитать корни уравнения

Если (a == 0) и (b == 0) и (c  0)

2.1. Вывести «Уравнение задано неверно»

Если (a == 0) и (b == 0) и (c == 0)

2.2. Вывести «x – любое число»

Если (a == 0) и (b  0)

2.3. Рассчитать корень линейного уравнения

Если (a  0)

2.4. Рассчитать корни квадратного уравнения

2.3. Рассчитать корень линейного уравнения

2.3.1. Рассчитать корень уравнения: x= -c/b

2.3.2. Вывести «Корень линейного уравнения x= <x>»

2.4. Рассчитать корни квадратного уравнения

2.4.1. Рассчитать дискриминант D= b*b - 4*a*c

2.4.2. Рассчитать действительные корни квадратного уравнения согласно дискриминанту D

2.4.2. Рассчитать действительные корни квадратного уравнения согласно дискриминанту D

Если D > 0

2.4.2.1. Рассчитать два корня квадратного уравнения

Если D == 0

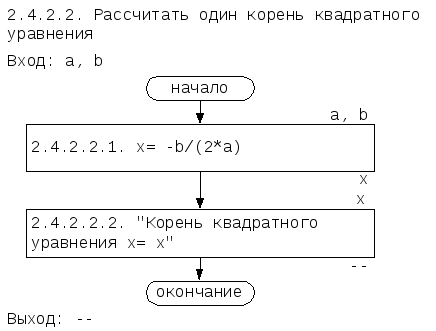
2.4.2.2. Рассчитать один корень квадратного уравнения

Если D < 0

2.4.2.3. Вывести «Нет действительных корней квадратного уравнения»

2.4.2.1. Рассчитать два корня квадратного уравнения

2.4.2.1.1. x1= (-b + D)/(2*a)

2.4.2.1.2. x2= (-b - D)/(2*a)

2.4.2.1.3. Вывести «Корни квадратного уравнения x1= <x1> и x2= <x2>»

2.4.2.2. Рассчитать один корень квадратного уравнения

2.4.2.2.1. x= -b/(2*a)

2.4.2.2.2. Вывести «Корень квадратного уравнения x= <x>»

Окончание занятия №4 (лекция)

Тестирование (трассировка) алгоритма

Основной задачей данного этапа является проверка работоспособности алгоритма и исправление ошибок. Идея тестирования заключается в ручном выполнении алгоритма по шагам. Для проверки работоспособности алгоритма используются тестовые примеры: из них берутся исходные данные и контролируются значения промежуточных и конечных данных.

Тестирование алгоритма происходит дискретно, т.е. каждая алгоритмическая структура тестируется отдельно. При этом должно выполняться следующее требование: каждая ветвь алгоритма должна быть протестирована хотя бы один раз, а цикл не менее трех раз.

В результате тестирования могут быть выявлены следующие ошибки:

– несовпадение входных и выходных данных по составу, типу и значениям;

– пропущено действие, имеется лишнее или ошибочное действие;

– неверен порядок действий;

– действие выполняется ошибочное количество раз;

– действие либо не выполняется при определенном условии, хотя должно выполняться, либо, наоборот, выполняется, когда не должно выполняться.

В зависимости от выявленных ошибок может произойти возврат к одному из предыдущих шагов проектирования программы: постановке задачи, разработке тестовых примеров, разработке структуры данных и составлению алгоритма.

Пример:

Блок-схемы и трассировка

Пример:

Блок-схема и трассировка циклов

Окончание занятия №5 (лекция)

Кодирование алгоритма. Форматирование кода.

После того как алгоритм проверен и представлен в словесной форме или в виде блок-схем его можно записать на языке программирования. Делается это путем представления каждой алгоритмической структуры в виде определенной последовательности операторов языка (см. Приложение 1). Основное внимание при этом необходимо уделять правильному комментированию программы. Для этого используются следующие правила:

1) Все переменные должны быть закомментированы.

2) Комментироваться должны все основные шаги алгоритма. Излишние комментарии также не допускаются.

3) Комментарий должен пояснять смысл действия, а не «пересказывать» операторы языка программирования. Например, вместо комментария «увеличиваем переменную i на единицу» должен быть использован комментарий «переходим к следующему элементу массива».

Окончание занятия №6 (практика)