
- •Варианты рассуждений
- •Законы силлогистики
- •Формальные системы
- •Понятие формальной системы
- •Интерпретация формальной системы
- •Истинность формальной системы
- •Ограничения формальных систем
- •Исчисление высказываний
- •Исчисление высказываний как формальная система
- •Доказательство выводимости формул
- •Синтаксический подход к доказательству вывода формул
- •Семантический подход к доказательству вывода формул
- •Синтаксический подход к доказательству вывода формул. Доказательство методом резолюции
- •Исчисление предикатов первого порядка
- •Отличия исчисления предикатов первого порядка от исчисления высказываний
- •Исчисление предикатов как формальная система
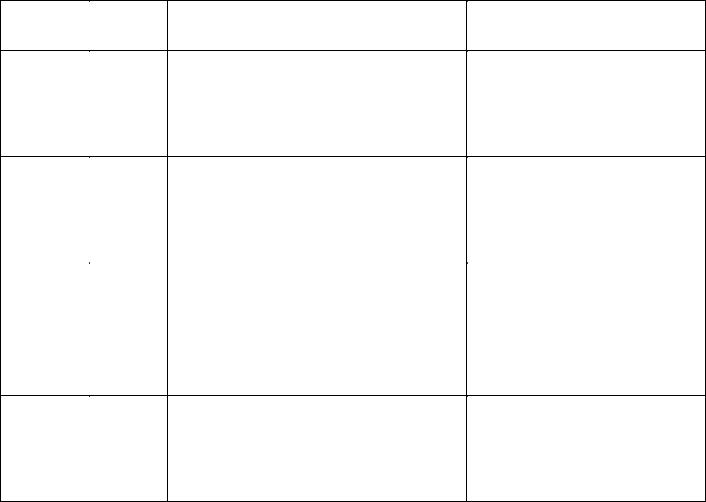
Доказа- |
Истин- |
Пример |
Причина противоречия |
|
тельство |
ность |
|||
|
|
|||
теорема |
истина |
Исходя из аксиом «Все птицы от- |
|
|
|
|
кладывают яйца» и «Пингвин – |
|
|
|
|
птица», имеется теорема «Пингви- |
|
|
|
|
ны откладывают яйца» |
|
|
теорема |
ложь |
Исходя из аксиом «Все птицы ле- |
Неверные аксиомы и пра- |
|
|
|
тают» и «Пингвин – птица», имеет- |
вила вывода, не отражаю- |
|
|
|
ся теорема «Пингвины летают» |
щие закономерности пред- |
|
|
|
|
метной области |
|
нетеоре- |
истина |
Исходя из аксиом «Все птицы от- |
Неполнота аксиом и невер- |
|
ма |
|
кладывают яйца» и «Пингвин – |
ные правила вывода с точ- |
|
|
|
птица», нельзя доказать, что |
ки зрения предметной обла- |
|
|
|
«Страусы откладывают яйца», хотя |
сти |
|
|
|
это истина |
|
|
нетеоре- |
ложь |
Исходя из аксиом «Все птицы от- |
|
|
ма |
|
кладывают яйца» и «Пингвин – |
|
|
|
|
птица», нельзя доказать, что «Пин- |
|
|
|
|
гвины не откладывают яйца» |
|
Возможны формальные системы, в которых аксиомы порождают ложные теоремы, т.е. с синтаксической точки зрения все верно, а с семантической нет. Возможна ситуация и наоборот.
Главная цель построения формальной системы — построить такую формальную систему, в которой теоремы всегда истинны, а нетеоремы всегда ложны, и имеется эффективный алгоритм разрешимости формальной системы.
Ограничения формальных систем
Применение формальных систем на практике имеет ряд ограничений, которые сформулированы в виде самых общих теорем.
Теорема Геделя: Возможны формальные системы, в которых существуют формулы m, такие что ни m ни ¬m не являются доказуемыми.
19
Теорема Тарского: Возможны формальные системы, в которых во всякой интерпретации найдутся выражения истинные, но недоказуемые.
Теорема Черча: Возможны формальные системы, в которых не существует алгоритма, чтобы отличить теоремы от нетеорем.
20
