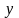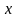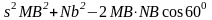Методические указания К РЕШЕНИЮ ЗАДАЧ
Математика – это наука о пространственных формах и количественных отношениях в самом общем виде, - прошла большой путь развития одновременно с развитием цивилизации и стала неотъемлемой частью культуры человечества и показателем интеллектуального уровня общества. Помимо собственных потребностей развития математика обслуживает потребности многих других наук – естественных, технических, экономических, гуманитарных. С развитием вычислительной техники область использования математики расширяется. В наше время трудно представить себе хорошего специалиста в области экономики, не знающего основных математических методов и математического языка. Поэтому математика включена в учебные планы всех экономических специальностей и ее изучению отводится немало времени.
Для успешного изучения математики необходимы программа, учебники и учебные пособия, справочная литература, таблицы, инженерный микрокалькулятор и, конечно, волевые усилия. Необходимо посещать все очные занятия в период сессий и стремиться самостоятельно, выполнять контрольные работы, пользуясь руководствами к решению задач, методическими указаниями и конспектами практических занятий.
Предлагаемые «Методические указания» должны помочь студенту рационально организовать свой труд по изучению математики и выполнению контрольных работ.
Методические указания к решению задач
Для того, чтобы облегчить студенту самостоятельное выполнение контрольных работ, приведем примеры решений задач, аналогичных тем, какие предлагаются в контрольных работах.
Задачи раздела ΙΙ заданий
Задача
5. Найти производные
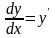 следующих функций
следующих функций
(дается
сложные и неявная функции): а)
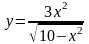
Решение.
По правилам дифференцирования дроби получим
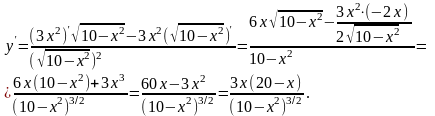
б)
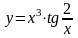 .
.
Решение.
По правилам дифференцирования произведения получим
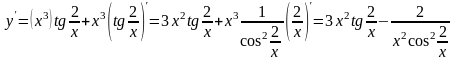
в)
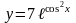
Решение.
Дифференцируем как сложную функцию.
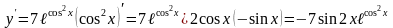
г)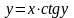 .
Это неявная функция.
.
Это неявная функция.
Решение.
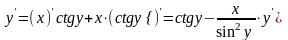
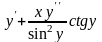 ,
,
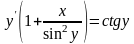 ,
,
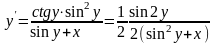 .
.
Задача 6. С помощью правила Лопиталя вычислить пределы функций:
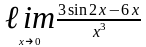 .
.
Решение.
Непосредственная
подстановка х = 0 приводит к неопределенности
вида
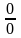 ,
следовательно, можно применить правило
Лопиталя: заменить предел отношения
функций пределом отношения их производных.
,
следовательно, можно применить правило
Лопиталя: заменить предел отношения
функций пределом отношения их производных.
Решение.
При
 получим неопределенность вида
получим неопределенность вида
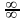 ,
когда можно применить правило Лопиталя.
,
когда можно применить правило Лопиталя.
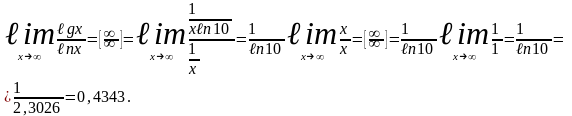
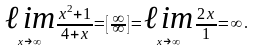
Задача
7. Исследовать функцию
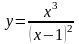 и построить ее график.
и построить ее график.
Решение.
Исследование выполним по примерной схеме, имеющейся в учебниках и практических руководствах. График можно строить либо по ходу исследования, либо конце исследования (рис.2).
Функция общего вида.
|
|
Вертикальная
асимптота может быть в точке разрыва
или на границе области определения.
Здесь вертикальная асимптота
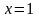 .
.
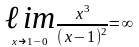 , - предел слева в точке
, - предел слева в точке
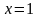 ;
;
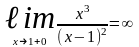 - предел справа. Наклонные асимптоты
вида
- предел справа. Наклонные асимптоты
вида
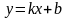 Найдем, если существуют конечные пределы
Найдем, если существуют конечные пределы
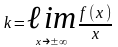 и
и
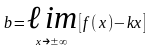 .
.
Здесь
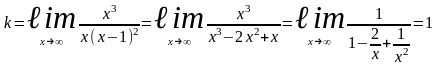
Итак,
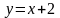 - уравнение наклонной асимптоты.
- уравнение наклонной асимптоты.
Найти интервалы монотонности (возрастания и убывания) функции и точки экстремума.
Найдем производную первого порядка.
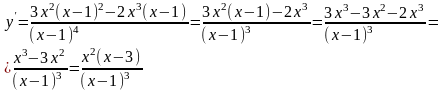
Найдем
критические точки первого рода и выясним
знаки
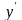 на полученных интервалах в окрестности
критических точек. Критические точки:
х1
= 0, х2
= 3, х3
= 1 - последняя н входит в область
определения функции. Используя достаточные
признаки экстремума, выясним, как меняет
знак
при
переходе через критические точки слева
направо. Возьмем непрерывный интервал
на полученных интервалах в окрестности
критических точек. Критические точки:
х1
= 0, х2
= 3, х3
= 1 - последняя н входит в область
определения функции. Используя достаточные
признаки экстремума, выясним, как меняет
знак
при
переходе через критические точки слева
направо. Возьмем непрерывный интервал
 ,
содержащий точку
.
,
содержащий точку
.
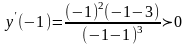 ;
;
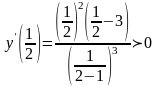 .
Так как при переходе через точку
производная
знак не имеет, то функция монотонно
возрастает и
не является точкой экстремума.
.
Так как при переходе через точку
производная
знак не имеет, то функция монотонно
возрастает и
не является точкой экстремума.
Возьмем
интервал
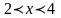 ,
содержащий точку х = 3.
,
содержащий точку х = 3.
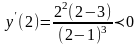 ;
;
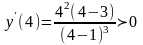 .
Здесь производная меняет знак с «-» на
«+», значит, х =3 – точка минимума функции
.
Здесь производная меняет знак с «-» на
«+», значит, х =3 – точка минимума функции
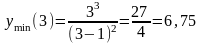 .
.
Итак,
функция возрастает на интервалах
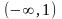 и
и
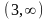 ,
убывает на интервале (1;3).
,
убывает на интервале (1;3).
Найти интервалы выпуклости и вогнутости графика функции и точки перегиба.
Вычислим производную второго порядка и найдем критические точки второго рода.
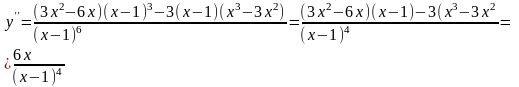 Критические
точки второго рода, при которых
Критические
точки второго рода, при которых
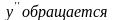 в нуль или существует, такие
в нуль или существует, такие
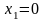 ,
,
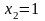 ,
но эта последняя не входит в область
определения функции. Остается точка х
= 0. Проверим меняет ли знак
,
но эта последняя не входит в область
определения функции. Остается точка х
= 0. Проверим меняет ли знак
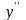 при переходе через эту точку. Возьмем
интервал (-1;
при переходе через эту точку. Возьмем
интервал (-1;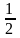 ),
содержащий точку х = 0. Вычислим
),
содержащий точку х = 0. Вычислим
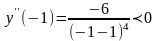 ,
,
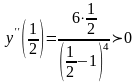 .
Отсюда следует, что х = 0 – точка перегиба,
.
Отсюда следует, что х = 0 – точка перегиба,
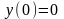 .
.
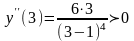 .
Отсюда следует, что
.
Отсюда следует, что
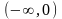 - интервал выпуклости;
- интервал выпуклости;
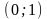 ,
,
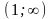 - интервалы вогнутости кривой.
- интервалы вогнутости кривой.
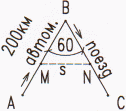
Задача 8. Три пункта А.В. и С расположены так, что угол АВС (рис.3) равен 600. Расстояние между пунктами А и В равно 200 км. Одновременно из пункта А выходит автомобиль, а из пункта В – поезд. Автомобиль движется по направлению к пункту В со скоростью 80 км/ч, а поезд движется по направлению к пункту С со скоростью 50 км/ч. Через скорость времени расстояние между автомобилем и поездом будет наименьшим?
Решение.
|
Пусть
t-время,
через которое, поле начала движения
автомобиля и поезда, расстоянием MN
= s
между ними будет наименьшими. По
теореме косинусов для треугольника
MBN
запишем равенство
H0 MB = 200 – 80t, NB = 50t, cos600 = .
|
рис. 3.
Тогда
получим уравнение
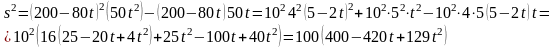 ;
;
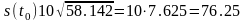 км.
км.
Отсюда
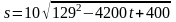 .
Найдем первую производную по t:
.
Найдем первую производную по t:
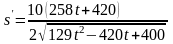 .
Приравнивая первую производную к нулю
получим
.
Приравнивая первую производную к нулю
получим
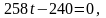 откуда
откуда
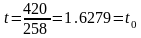 или
или
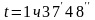 -
критическая точка.
-
критическая точка.
Квадратный
трехчлен под корнем в знаменателе в
ноль не обращается ни при каких
действительных значениях t,
поскольку его дискриминант Д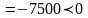 .
.
Легко
видеть, что при переходе через критическую
точку t0
от меньших значений t
к большим, например, от t
= 1 до t
= 2, первая производная меняет знак с
минуса на плюс
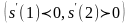 .
Следовательно, t0
= 1.6279 часа – точка минимума функции s.
А так как других экстремумов эта функция
не имеет, то в точке минимума функция
имеет наименьшее значение:
.
Следовательно, t0
= 1.6279 часа – точка минимума функции s.
А так как других экстремумов эта функция
не имеет, то в точке минимума функция
имеет наименьшее значение:
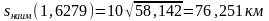 .
.
Задача
11. Найти неопределенные интегралы
а)
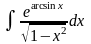 ,
б)
,
б)
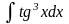 ,
,
в)
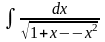 ,
г)
,
г)
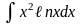 ,
д)
,
д)
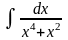 .
.
Предлагаемые интегралы можно , применив основные методы
интегрирования; метод замены переменной подстановка, метод
интегрирования по частям.

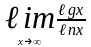



 бласть
определения функции
бласть
определения функции
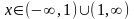 .
.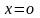 ,
тогда
,
тогда
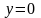 .
Пусть
,
тогда
.
Пусть
,
тогда
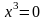 или
или
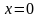 .
Значит, график функции проходит через
начало координат.
.
Значит, график функции проходит через
начало координат.
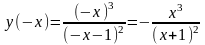 .
.