Критерий сходимости последовательности.

Для того чтобы у последовательности существовал предел, необходимо и достаточно, чтобы последовательность имела только один частичный предел.

1. Пусть . Тогда для , т.е. у имеется единственный предел, равный a.

2. Пусть у имеется только один частичный предел, равный a. Если , то вне некоторой окрестности ­ будет лежать бесконечно много , например, бесконечно много ­ . Рассмотрим последовательность , но такую, что . У существует частичный предел . Т.к. , то B – также частичный предел , и . По заданному условию у не может быть двух частичных пределов, значит, .

Для сходимости необходимо и достаточно, чтобы имела один частичный предел и была ограничена.

1. Пусть сходится, тогда имеет единственный частичный предел и ограничена.

2. Пусть имеет единственный частичный предел, равный a и ограничена, т.е. и . Тогда и , т.е. сходится.

Для сходимости необходимо и достаточно чтобы и была ограничена.

1. Пусть . Тогда у единственный частичный предел a и . Кроме того, ограничена, т.к.

2. Пусть и ограничена. Тогда у имеется единственный частичный предел, равный a, значит, и, т.к. ограничена, то .

Последовательность называется фундаментальной, если для для и любого натурального числа m выполняется неравенство .

Критерий Коши сходимости последовательностей: Для сходимости последовательности необходимо и достаточно, чтобы она была фундаментальной.

1. Пусть . Возьмём . По определению предела для конечного a для буде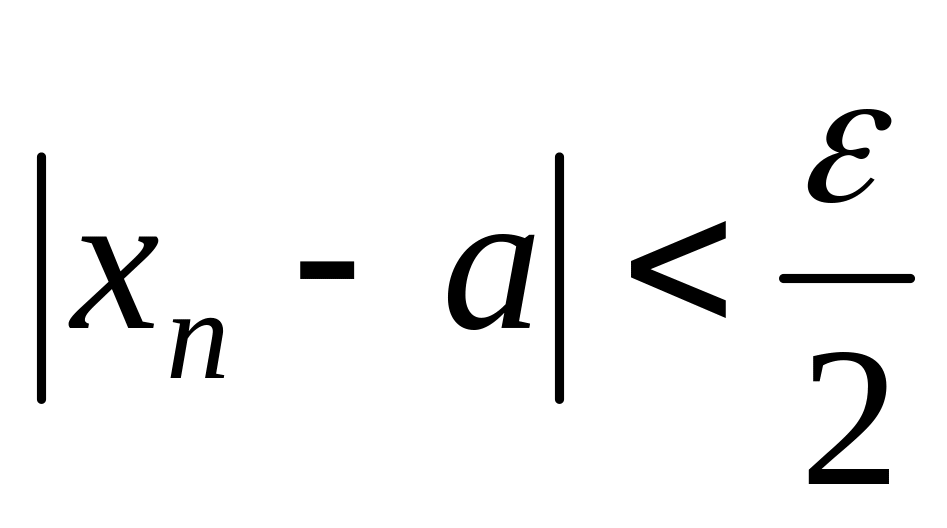т . Тогда и для любого натурального m будет и, значит, . Отсюда для и любого натурального m будет , т.е. – фундаментальная.

2. Пусть – фундаментальная. Докажем, что ограничена и . Отсюда будет следовать её сходимость.

   1. Докажем ограниченность. Возьмём . Тогда для и любого натурального m будет . Зафиксируем . Тогда для любого натурального m будет . Отсюда , откуда для и любого натурального m. Положим . Тогда для , т.е. ограничена.

   2. Докажем, что . По определению фундаментальной последовательности для для и будет , т.е. . Следовательно, . Тогда для будет (если бы , то достаточно взять , чтобы прийти к противоречию).

   3. Т.к. последовательность ограничена и , то имеет конечный предел.

Предел функции и его свойства

Точка a называется предельной точкой множества A, если в любой окрестности числа a находится хотя бы одна точка .

Первое определение предела функции: Пусть определена на множестве A и a – предельная точка A. Говорят, что , если для для и будет . Если, например, и , то для для будет .

Второе определение предела функции: Пусть определена на множестве A и a – предельная точка. Говорят, что , если для будет .

Оба определения функции равносильны.

1. Пусть предел функции определён первым способом. То есть возьмём и тогда для будет . Возьмём . Тогда по определению предела последовательности для будет . Следовательно, для будет . Значит, при , т.е. определён вторым способом.

2. Пусть теперь предел функции определён вторым способом. Предположим, что по первому определению, т.е. для , но . Возьмём . Тогда должны существовать такие, что 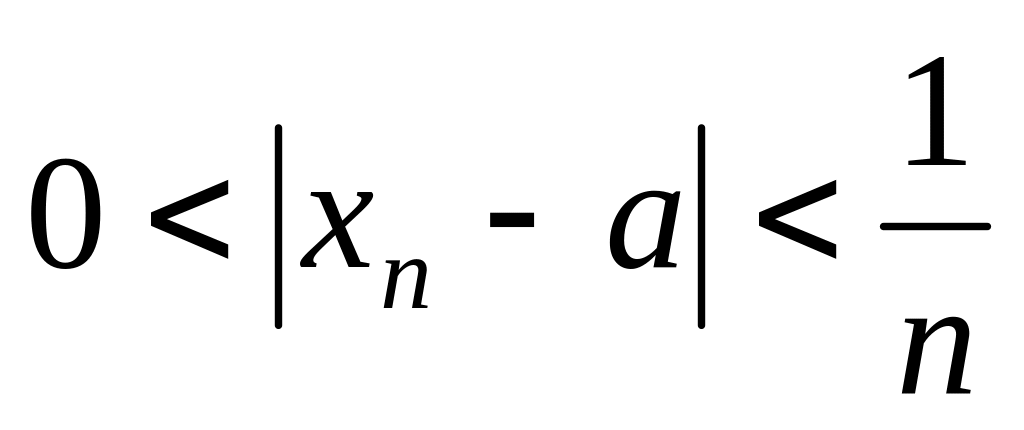, т.е. при , но , т.е. , что противоречит определению.

Пусть существует конечные и . Тогда

1. .

2. .

3. Если то .

Возьмём . Тогда, по условию, . Поэтому , .

В определении предела функции вторым способом достаточно требовать, чтобы существовал для . Равенство значений этих пределов получится автоматически.

Пусть в некоторой окрестности точки a, возможно, исключая само a будет , . Тогда .

Возьмём . Тогда и . Отсюда при . Ввиду произвольности это значит, что .

Критерий Коши для функции: Для того чтобы существовал конечный необходимо и достаточно, чтобы для для и и . (для ) выполнялось бы неравенство .

1. Пусть существует . Рассмотрим, например, конечное a. Тогда для для будет . Возьмём и такие, что , . Тогда .

2. Пусть выполняется условие теоремы. Рассмотрим, например, случай конечного a. Возьмём . По условию для и будет . Возьмём для и натурального будет , откуда . Следовательно, фундаментальна, значит, она сходится, откуда следует, что существует конечный .

Функция называется непрерывной в точке a, если либо определена в некоторой окрестности точки a и ­ , либо такое, что в интервале не определена.

Теорема: .

, т.е. или . Поделив эти неравенства на , получим: . При . Тогда и для . Заметим, что для , если положить будет , , , т.е. . Значит для .

Теорема: .

1. Возьмём . Пусть, сначала, такова, что – натуральные числа. Докажем, что в этом случае . Мы знаем, что 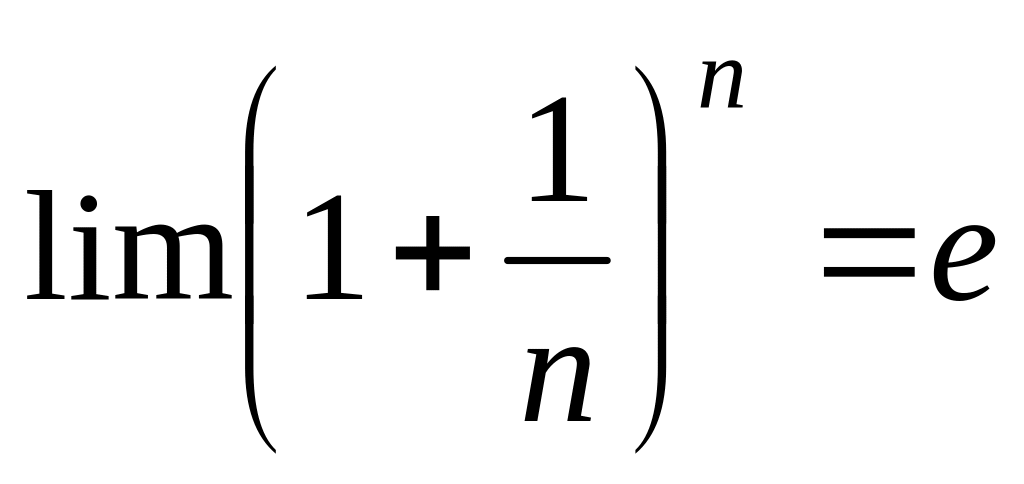. Возьмём и найдём для . Т.к. и – натуральные числа, то для K найдётся такое, что для будет и, следовательно, для будет . Это значит, что .

2. Пусть теперь произвольно. Можно считать, что . Обозначим . Тогда . Тогда . И, значит, . Т.к. и – натуральные, то . Аналогично .

3. Пусть теперь . Обозначим . Тогда . Имеем .

Говорят, что ­ имеет в точке a левосторонний предел , если a – предельная для множества определения и если будет для случая конечного выполнено условие: для из условия будет следовать . Для – для для будет .

не убывает на множестве A, если для и из следует .

возрастает на множестве A, если для и из следует .

П усть определена на промежутке X, точка (или является его правым концом (для случая предела слева)) и пусть не убывает на X. Если ограничена на сверху, то существует конечный предел . Если же на не ограничена сверху, то .

Пусть, например, ограничена сверху на . Тогда существует . Докажем, что . Возьмём . Тогда и . Пусть . Тогда, если , то будет , а, значит, , т.е. . Следовательно, .