Санкт-Петербургский государственный технологический институт

(Технический университет)

Кафедра САПРиУ

Курс 3

Группа 4893

Отчёт по лабораторной работе №4

«Изучение прямых и косвенных оценок качества регулирования»

Исполнители:

Ясевич Т.

Волкова Е.

Лозовенков В.

Руководители:

Гольцева Л..В.

Макарова Л.Ф.

Санкт-Петербург, 2011

Цель работы: определение и анализ частотных оценок качества регулирования; установление связи между косвенными и прямыми оценками качества; сравнение прямых оценок качества, рассчитанных по формулам и полученных непосредственно по графикам переходных процессов.

Задание:

Исследовать качество регулирования одноконтурной АСР с помощью прямых и косвенных оценок качества, используя программную систему OCENKA.

Рисунок 1 Структурная схема АСР

k_об = 1, T₁ = 10, T₂ =20, T₃ =20

k_рег(T_изp+1) k_об

W_рег(p) = ; W_об(p) =

T_изp (T₁p+1)(T₂p+1)(T₃p+1)

1. Вывести характеристическое уравнение замкнутой системы.

Передаточная функция замкнутой системы имеет вид:

Передаточная функция разомкнутой системы представляет собой произведение передаточных функций последовательно соединённых звеньев регулятора и объекта:

.

Характеристический полином замкнутой системы равен сумме числителя и знаменателя передаточной функции разомкнутой системы:

=0

Раскроем скобки, приведем подобные и получим следующий вид характеристического полинома:

После подстановки исходных данных характеристический полином будет иметь следующий вид:

D(p)=4000*T_из*р⁴+800*Т_из*р³+250*Т_из*р²+Т_из*р+k_рег*k_об*(Т_из*р+1)

2. Построим кривые d-разбиения для нашей аср

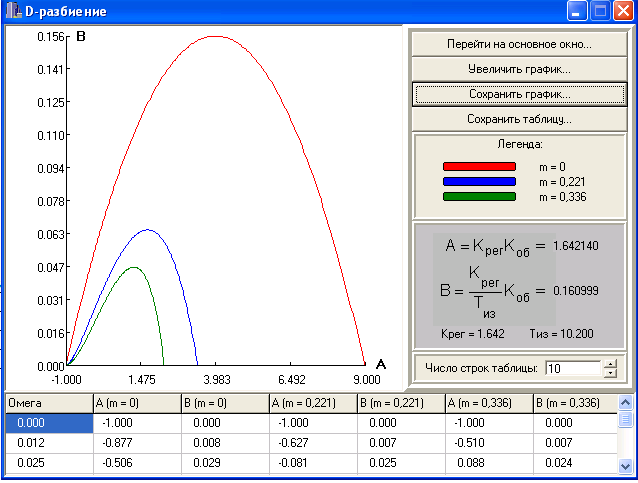
Рисунок 2 – Кривые D-разбиения

Выбираем точки, располагающиеся на специальной кривой K_р:

№ точки	Крег	Тиз
1	0.171	7.183
2	0.371	12.814
3	0.605	16.995

5. 3. Графики афх для каждой исследуемой точки.

Рисунок 3 – АЧХ замкнутой АСР для первой точки

Рисунок 4 – АЧХ замкнутой АСР для второй точки

Рисунок 5 – АЧХ замкнутой АСР для третей точки

4. Определяем по графикам ачх частотные характеристики аср: резонансную частоту ωр , частоту среза ωср , диапазон пропускаемых системой частот (0 - ωо) , показатель колебательности m.

Резонансная частота – это частота, при которой АЧХ замкнутой САУ имеет максимум A_зmax( ) На этой частоте гармонические колебания проходят через систему с наибольшим усилением. Резонансная частота замкнутой системы близка к частоте колебаний сис­темы в переходном процессе. Значение может быть приближенно определе­но по точке АФХ которая ближе всего расположена к точке (-1; j·0).

Частота среза – при этой частоте АЧХ системы принимает значение, равное 1, т.е. A_з( )=1. Эта частота косвенно характеризует длительность переходного процесса. Чем меньше , тем хуже быстродействие системы. Величина зависит от инер­ционности объекта и зоны нечувствительности прибора, измеряющего колеба­ния выходной величины. Чем они больше, тем меньше .

Диапазон пропускаемых системой частот – это интервал частот от =0 до при котором выполняется условие A_з( ) = 0.707A_з(0) или при A_з(0) = 1 величина A_з( ) = 0.707. Полоса пропускания не должна быть слишком широкой, иначе система будет воспроизводить высокочастотные помехи, и в то же время не может быть слиш­ком узкой, иначе система не сможет пропускать полезный сигнал.

Показатель колебательности определяется М как отношение максимального значения АЧХ замкнутой системы А_зmax( ) к ее значению при =0. М характеризует склонность системы к колебаниям. В общем случае при М<1 переходная характеристика системы не колебательна. Чем выше М, тем больше колебательность, т.е. тем менее качественна система при прочих равных услови­ях. При A_з( ) M и колебательность возрастает до получения неза­тухающих с частотой , колебаний, соответствующнх границе устойчивости САУ ( передаточная функция замкнутой системы имеет пару сопряженных мнимых полюсов ±j ).

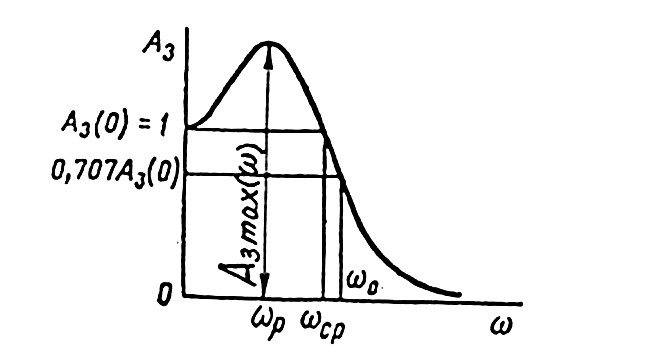
Рисунок 6 – Определение по графику , ,

№ точки			0 -	M
1	0.023	0.0234	0 - 0.0236	1.394
2	0.027	0.0267	0 – 0.031	1.398
3	0.03	0.0301	0 – 0.032	1.467

Из таблицы видно, что значение показателя колебательности первой и второй точки лежит в интервале , что является допустимым. Известно, что чем выше показатель колебательности, тем менее качественна система.