16.3. Предел функции при х  ∞

Пусть функция у=ƒ(х) определена в промежутке (-∞;∞). Число А называется пределом функции ƒ(х) при х→∞, если для любого положительного числа ε существует такое число М=М()>0, что при всех х, удовлетворяющих неравенству |х|>М выполняется неравенство |ƒ(х)-А|<ε. Коротко это определение можно записать так:

Геометрический смысл этого определения таков: для ε>0   М>0, что при х є(-∞; -М) или х є(М; +∞) соответствующие значения функции ƒ(х) попадают в ε-окрестность точки А, т. е. точки графика лежат в полосе шириной 2ε, ограниченной прямыми у=А+ε и у=А-ε (см. рис. 112).

16.4. Бесконечно большая функция (б.Б.Ф.)

Функция у=ƒ(х) называется бесконечно большой при х→х₀, если для любого числа М>0 существует число δ=δ(М)>0, что для всех х, удовлетворяющих неравенству 0<|х-хо|<δ, выполняется неравенство |ƒ(х)|>М.

Например, функция у=1/(х-2) есть б.б.ф. при х—>2.

Если ƒ(х) стремится к бесконечности при х→х_о и принимает лишь положительные значения, то пишут

если лишь отрицательные значения, то

Функция у=ƒ(х), заданная на всей числовой прямой, называется бесконечно большой при х→∞, если для любого числа М>0 найдется такое число N=N(M)>0, что при всех х, удовлетворяющих неравенству |х|>N, выполняется неравенство |ƒ(х)|>М. Коротко:

Например, у=2х есть б.б.ф. при х→∞.

Отметим, что если аргумент х, стремясь к бесконечности, принимает лишь натуральные значения, т. е. хєN, то соответствующая б.б.ф. становится бесконечно большой последовательностью. Например, последовательность v_n=n²+1, n є N, является бесконечно большой последовательностью. Очевидно, всякая б.б.ф. в окрестности точки х_о является неограниченной в этой окрестности. Обратное утверждение неверно: неограниченная функция может и не быть б.б.ф. (Например, у=хsinх.)

Однако, если limƒ(х)=А при х→x₀, где А — конечное число, то функция ƒ(х) ограничена в окрестности точки х_о.

Действительно, из определения предела функции следует, что при х→ х₀ выполняется условие |ƒ(х)-А|<ε. Следовательно, А-ε<ƒ(х)<А+ε при х є (х_о-ε; х_о+ε), а это и означает, что функция ƒ (х) ограничена.

Свойства пределов функции

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

Аналогично предел разности двух функций равен разности пределов этих функций.

Расширенное свойство предела суммы:

Предел суммы нескольких функций равен сумме пределов этих функций:

Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

Расширенное свойство предела произведения

Предел произведения нескольких функций равен произведению пределов этих функций:

5) Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

Определение 2.11   Первым замечательным пределом называется предел

    

        Теорема 2.14   Первый замечательный предел равен

        Доказательство.     Рассмотрим два односторонних предела и и докажем, что каждый из них равен 1. Тогда по теореме 2.1 двусторонний предел также будет равняться 1.

Итак, пусть (этот интервал -- одно из окончаний базы ). В тригонометрическом круге (радиуса ) с центром построим центральный угол, равный , и проведём вертикальную касательную в точке пересечения горизонтальной оси с окружностью ( ). Обозначим точку пересечения луча с углом наклона с окружностью буквой , а с вертикальной касательной -- буквой ; через обозначим проекцию точки на горизонтальную ось.

Рис.2.27.Тригонометрический круг

Пусть  -- площадь треугольника ,  -- площадь кругового сектора , а  -- площадь треугольника . Тогда очевидно следующее неравенство:

Заметим, что горизонтальная координата точки равна , а вертикальная -- (это высота треугольника ), так что . Площадь центрального сектора круга радиуса с центральным углом равна , так что . Из треугольника находим, что . Поэтому Неравенство, связывающее площади трёх фигур, можно теперь записать в виде

Все три части этого неравенства положительны, поэтому его можно записать так:

или (умножив на ) так:

Предел постоянной 1 в правой части неравенства, очевидно, равен 1. Если мы покажем, что при предел в левой части неравенства тоже равен 1, то по теореме "о двух милиционерах" предел средней части также будет равен 1.

Итак, осталось доказать, что . Сперва заметим, что , так как равняется длине дуги окружности , которая, очевидно, длиннее хорды . Применяя теорему "о двух милиционерах" к неравенству

при , получаем, что

(2.3)

Простая замена переменной показывает, что и . Теперь заметим, что . Применяя теоремы о линейности предела и о пределе произведения, получаем:

(2.4)

Тем самым показано, что

Сделаем теперь замену ; при этом база перейдёт в базу (что означает, что если , то ). Значит,

но (  -- нечётная функция), и поэтому

Мы показали, что левосторонний предел также равен 1, что и завершает доказательство теоремы.     

Доказанная теорема означает, что график функции выглядит так:

Рис.2.28.График

Приведём примеры применения первого замечательного предела для вычисления других родственных пределов.

        

        

    

        Пример 2.20   Вычислим предел .

Очевидно, что

при этом предел знаменателя был вычислен в предыдущем примере; он равен 1. Числитель правой части имеет предел 1. Применяя теорему о пределе отношения, получаем

    

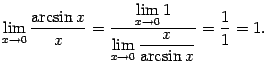
        Пример 2.21   Вычислим предел .

Преобразуем функцию под знаком предела следующим образом:

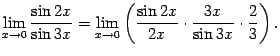
Теперь вынесем постоянный множитель за знак предела и применим теорему о пределе произведения:

(Чуть ниже мы увидим, что пределы сомножителей существуют, так что применять эту теорему здесь можно.) Заметим, что при заменах и база переходит в базу и , так что

и

Поэтому

    

        Определение 2.12   Вторым замечательным пределом называется предел

    

Число , заданное этим пределом, играет очень большую роль как в математическом анализе, так и в других разделах математики. Число часто называют основанием натуральных логарифмов.

        Теорема 2.15   Второй замечательный предел существует. Его значение  -- число, лежащее между и .    

Более подробное изучение числа показывает, что  -- иррациональное число, несколько первых десятичных знаков которого таковы:

Для доказательства теоремы 2.15 нам понадобится следующая лемма; формула, в ней полученная, называется формулой бинома Ньютона.

        Лемма 2.2   Пусть и  -- натуральное число. Тогда имеет место формула

Заметим, что в дроби

очевидно, сокращаются все сомножители в числителе и знаменателе, так что эта дробь равна 1. Аналогично, в предыдущем (не выписанном) слагаемом после сокращения получается коэффициент, равный , в третьем справа слагаемом -- равный , и т. д. Таким образом, коэффициенты в слагаемых, стоящих на одинаковых местах, считая слева и справа от края формулы, совпадают.

        Доказательство.     Доказывать утверждение леммы будем по индукции по параметру . При формула 2.2, очевидно, верна:

(Заметим, что при и формула 2.2 также хорошо известна:

и

Предположим, что она верна для , и докажем, что тогда она верна и при . Действительно,

При этом в квадратных скобках получается:

и так далее, то есть как раз то, что должно получиться в качестве коэффициентов формулы бинома Ньютона при .     

        Доказательство теоремы 2.15.     Рассмотрим последовательность и применим к формулу бинома Ньютона при и . Получим

Покажем, что последовательность ограничена сверху. Для этого заменим все дроби , , ..., на 1. Все эти дроби меньше 1, так что сумма в правой части формулы (Доказательство теоремы 2.15) увеличится:

Далее, заменим все числа в знаменателях этих слагаемых на 2; от этого правая часть ещё увеличится. Получим:

В правой части получилась сумма членов геометрической прогрессии. Она равна

Поэтому

что и означает ограниченность последовательности сверху числом 3.

Покажем теперь, что последовательность не убывает. Действительно, запишем формулу (Доказательство теоремы 2.15) в виде

В аналогичной формуле, написанной для вместо , во-первых, увеличится каждое из выражений в круглых скобках (так как вычитаемое уменьшится) и, значит, увеличатся все слагаемые, содержащие такие скобки. Во-вторых, число слагаемых увеличится на одно: добавится положительное слагаемое

Следовательно, при росте номера члены последовательности строго возрастают: при всех .

Применим теперь к возрастающей ограниченной сверху последовательности теорему о пределе монотонной ограниченной функции ( теорема 2.13) и получим, что существует предел

причём число не больше постоянной 3, ограничивающей последовательность. Осталось заметить, что . Так как все последующие члены ещё больше, то и предел , на основании теоремы о переходе к пределу в неравенстве ( следствие 2.7), не меньше числа , что и завершает доказательство теоремы.     

        

        

       Вот ещё один пример на раскрытие неопределённости вида .

        Пример 2.23   Найдём предел .

Здесь основание степени имеет предел

а показатель степени . Поэтому можно применять тот же приём сведения ко второму замечательному пределу, что в предыдущем примере. Для начала найдём, что следует взять за бесконечно малую величину . Поскольку основание степени стремится к 1, то оно равно , где (см.  теорему 2.4). Значит,

Теперь преобразуем функцию, стоящую под знаком предела:

Выражение, стоящее в квадратных скобках, имеет вид и при стремится к числу (это второй замечательный предел), а предел показателя степени мы найдём отдельно:

Поэтому

(Мы воспользовались тем, что если и , то . Это следует из непрерывности показательной и логарифмической функций, если учесть, что .)