16. Предел функции

16.1. Предел функции в точке

Пусть функция у=ƒ (х) определена в некоторой окрестности точки х_о, кроме, быть может, самой точки х_о.

Сформулируем два, эквивалентных между собой, определения предела функции в точке.

Определение 1 (на «языке последовательностей», или по Гейне).

Число А называется пределом функции у=ƒ(х) в топке x₀ (или при х х_о), если для любой последовательности допустимых значений аргумента x_n, n є N (x_nx₀), сходящейся к х_о последовательность соответствующих значений функции ƒ(х_n), n є N, сходится к числу А

В этом случае пишут       или ƒ(х)—>А при х→х_о. Геометрический смысл предела функции: означает, что для всех точек х, достаточно близких к точке х_о, соответствующие значения функции как угодно мало отличаются от числа А.

Определение 2 (на «языке ε», или по Коши).

Число А называется пределом функции в точке х_о (или при х→х_о), если для любого положительного ε найдется такое положительное число δ, что для все хх_о, удовлетворяющих неравенству |х-х_о|<δ, выполняется неравенство |ƒ(х)-А|<ε.

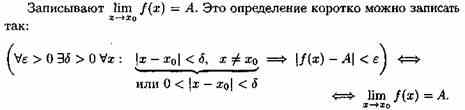
Геометрический смысл предела функции:

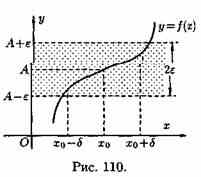
если для любой ε-окрестности точки А найдется такая δ-окрестность точки х_о, что для всех ххо из етой  δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у=А+ ε , у=А-ε (см. рис. 110). Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).

<< Пример 16.1

Доказать, что

Решение: Возьмем произвольное ε>0, найдем δ=δ(ε)>0 такое, что для всех х, удовлетворяющих неравенству |х-3| < δ, выполняется неравенство |(2х-1)-5|<ε, т. е. |х-3|<ε.

Взяв δ=ε/2, видим, что для всех х, удовлетворяющих неравенству |х-3|< δ, выполняется неравенство |(2х-1)-5|<ε. Следовательно, lim(2x-1)=5 при х –>3.

<< Пример 16.2

16.2. Односторонние пределы

В   определении   предела   функции считается, что х стремится к x₀ любым способом: оставаясь меньшим, чем x₀ (слева от х₀), большим, чем х_о (справа от х_о), или колеблясь около точки x₀.

Бывают случаи, когда способ приближения аргумента х к х_о существенно влияет на значение придела  функции. Поэтому вводят понятия односторонних пределов.

Число А₁ называется пределом функции у=ƒ(х) слева в точке х_о, если для любого число ε>0 существует число δ=δ(ε)> 0 такое, что при х є (х₀-δ;x_o), выполняется неравенство |ƒ(х)-А|<ε. Предел слева записывают так: limƒ(х)=А при х–>х₀-0 или коротко: ƒ(х_о-0)=А₁ (обозначение Дирихле) (см. рис. 111).

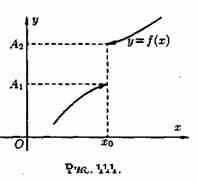
Аналогично определяется предел функции справа, запишем его с помощью символов:

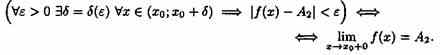
Коротко предел справа обозначают ƒ(х_о+0)=А.

Пределы функции слева и справа называются односторонними пределами. Очевидно, если существует  , то существуют и оба односторонних предела, причем А=А₁=А₂.

Справедливо и обратное утверждение: если существуют оба предела ƒ(х₀-0) и ƒ(х₀+0) и они равны, то существует предел  и А=ƒ(х₀-0).

Если же А₁А₂, то етот придел не существует.