22. Что такое ранг элемента и для чего он используется в сложных системах? Метод вычисления. Приведите пример.

Ранг вершины  это отношение количества достижимых путей, данной вершины с остальными вершинами к общему количеству достижимых путей в графе. Ранг позволяет распределить элементы системы в порядке их значимости. Вопрос о том, какой элемент более значимый, а какой  менее значимый встает тогда, когда необходимо распределить усилия по обеспечению надежности отдельных элементов в целях обеспечения заданной надежности системы. Иначе говоря, необходимо знать, какое влияние оказывает на общую надежность системы выход из строя или ошибочная работа того или иного элемента. На последующих этапах проектирования можно скорректировать параметр значимости, дополнив его параметрами функционирования системы.

Например, для графа, представленного на рис. 41, ранги вычисляются следующим образом:

0 1 1 1 1 1

0 0 1 1 0 1

0 1 0 1 0 1

0 1 1 0 0 1

0 1 1 1 0 1

0 0 0 0 0 0

= A^д

Рис. 41. Пример вычисления рангов вершин.

0 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1

0 0 1 1 0 1 0 0 1 1 0 1 0 0 1 1 0 1

0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1

R= A+A*A = 0 1 1 0 0 1 + 0 1 1 0 0 1 * 0 1 1 0 0 1 =

0 1 1 1 0 1 0 1 1 1 0 1 0 1 1 1 0 1

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

0 1 1 1 1 1 0 3 3 3 0 4 0 4 4 4 1 5 18

0 0 1 1 0 1 0 2 1 1 0 2 0 2 2 2 0 3 9

0 1 0 1 0 1 0 1 2 1 0 2 0 2 2 2 0 3 9

= 0 1 1 0 0 1 + 0 1 1 2 0 2 = 0 2 2 2 0 3 9

0 1 1 1 0 1 0 2 2 2 0 3 0 3 3 3 0 4 13

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

Получаем: R’={18,9,9,9,13,0}, R’=58 и ранги вершин равны соответ-ственно r₁=18/58=0.310, r₂=9/58=0.155, r₃=9/58=0.155, r₄=9/58=0.155, r₅=13/58=0.225, r₆=0. Как видно из полученных результатов, наибольшим рангом обладает вершина v₁, а наименьшим  вершина v₆.

23. Что такое свертка графа, как она осуществляется и как она связана со сложными системами? Приведите примеры.

При анализе сложных систем часто возникает необходимость перейти от графа системы к графу подсистем системы, т.е. объединить некоторые элементы системы по каким-то признакам или свойствам в подсистемы и исследовать взаимосвязь подсистем в системе Это задача свертки графа.

Пусть дан граф G=(V,U) и пусть P  количество вершин, Q  количество дуг графа. Пусть также каждой вершине vV сопоставлено K свойств и каждое свойство либо проявляется у элемента, обозначаемого вершиной, либо нет. Пусть задано какие значения свойств считаются важными, а какие несущественными, т.е. определена маска свойств.

Требуется перейти от графа G к графу G’=(V’,U’), |V’|=P’, |U’|=Q’, в котором каждая вершина получается объединением нескольких вершин исходного графа G в вершину v’V’ нового графа и имеющих одинаковое сочетание важных свойств, а каждая связь u’U’ получается объединением связей исходного графа G таким образом, что если две вершины были смежны в исходном графе и они объединились в разные вершины нового графа G’, то эти две вершины нового графа будут также смежны, а если объединились в одну вершину нового графа, то над этой вершиной будет петля.

С помощью свертывания графа можно переходить от исследования взаимосвязей элементов системы к исследованию взаимосвязей подсистем системы. Изменяя наборы глобальных и локальных свойств можно получать различные с точки зрения анализа структуры одной и той же системы, рассматривать систему как бы с разных позиций. В качестве свойств для свертки можно также использовать и структурные свойства графа системы.

Например, выше было рассмотрено разбиение графа на сильные компоненты связанности, которые являются замкнутыми подсистемами в сложной системе. Если вершинам присвоить номер той сильной компоненты связанности, к которой они принадлежат, и рассматривать этот номер как свойство вершины для свертки, то можно будет осуществить свертку графа системы, в результате которой получится граф, отражающий связи между замкнутыми подсистемами. Его дальнейшее исследование позволит изучить взаимодействие замкнутых подсистем.

24. Матричные способы представления графа. Пять вопросов по каждому представлению.

Матрицей смежности графа называется матрица V, имеющая размерность P*P, каждый элемент которой определяется следующим образом:

1 , если между i-ой вершиной и j-ой

V(i,j) = вершиной есть дуга ; (4)

0 , в противном случае.

Если на главной диагонали этой матрицы стоит единица, то это соответствует наличию петли в графе. Для графа представленного на рис. 1 представление имеет вид (см. рис. 15)

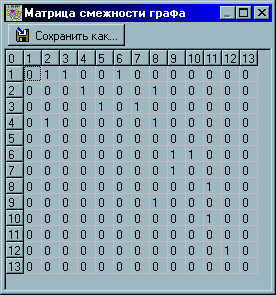
Рисунок 15. Матрица смежности графа

Данное представление является очень удобным и широко используемым на практике. Однако, в случае, когда Q < P*P это представление является не экономичным, поскольку требует много памяти для хранения нулей.

Матрицей инциденций графа называется матрица W, имеющая размерность P*Q, каждый элемент которой определяется следующим образом:

-1, если i-ая вершина — начало j-ой дуги;

W(i,j) = 1, если i-ая вершина — конец j-ой дуги; (5)