19. Что такое индекс избыточности по связям, степень центральности и как они связаны со сложными системами? Приведите примеры.

Индекс избыточности  это относительная разность числа связей Q, имеющихся в данной структуре, и числа связей Q_min, необходимого для того, чтобы в граф был связанным. Индекс избыточности используется для оценки связанности структур и интерпретируется как мера избыточности структуры системы по связям. Если граф содержит P вершин, то чтобы граф был связанным, необходимо Q_min=P1 дуг, независимо от того, является ли граф ориентированным или нет. Следовательно, для индекса избыточности  имеем формулу:

 = (Q  Q_min) / Q_min = (Q  (P  1)) / (P  1) = (Q / (P  1))  1

Е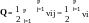 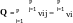сли граф дополнить любым числом изолированных вершин, то значение  останется прежним. Значение Q вычисляется по матрице смежности V для ориентированного и неориентированного графов по следующим формулам:

Для графа, представленного на рис. 34, имеем: P=8, Q=13 и получается =(2+2+3+2+2+2)/(81)1=13/71=0,857.

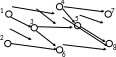
Рис. 34. Пример графа и его матрицы смежности.

Во многих задачах анализа важно определить как рассматривать реальную систему  относится она ближе к центральной или ближе к распределенной. Для этого удобно использовать такую обобщенную характеристику, как степень централизации структуры.

Степень централизации графа характеризует степень неравномер-ности загрузки элементов системы и вычисляется по формулам:

 = (P  1) (2 Z_max  P) / Z_max (P  2)

Z_max = max { 0.5   d_ij ( d_ij)  1 }

i i=1,P j=1,P j=1,P

где d_ij  это длина в дугах кратчайшего пути из i-ой вершины в j-ую вершину, при этом, если i=j, то d_ij=0 ;

P  количество вершин.

Если связи в структуре распределены равномерно рис. 35-а, то все вершины инцидентны одному и тому же числу ребер и =0. Если все вершины связаны с одной единственной  центральной рис. 35-б, то =1. В реальной системе 0<<1.

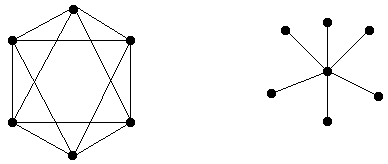а). Распределенная б).Центральная

Рис. 35. Централизованность структур.

Д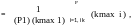 ля ориентированного графа индекс центральности вычисляется по формулам:

где _i  степень i-ой вершины, т.е. суммарное число входящих и исхо-дящих дуг ;

_k^max = max (_i )  это максимальная из степеней всех вершин.

i=1,P

20. Что такое сложность структуры? Как она вычисляется. Приведите пример.

Сложность графа структуры определяется по формуле:

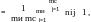
г

()

де m^и и т^с  количество вершин истоков и стоков в графе структуры ;

n_ij  количество различных путей, ведущих из i-ой вершины-истока в j-ю вершину-сток.

Как видно из формулы величина  численно равна уменьшенному на единицу среднему числу путей, ведущих из вершины-истока графа в вершину-сток, т.е. от входа системы к выходу. В структуре с минимальной сложностью из каждой вершины-истока можно попасть в вершину-сток единственным путем, и следовательно =0.

Для сложных графов, содержащих большое число путей, определить сложность структуры непосредственным перечислением путей довольно трудно. Поэтому для вычисления значения  графа без петель и контуров удобно использовать следующий алгоритм:

1. Исходный граф представляется в виде многоуровневого иерархического графа, в котором уровень иерархии каждой вершины определяется минимальным числом дуг, связывающих ее с истоками;

2. Иерархический граф, преобразуется в эквивалентный ему граф, не содержащий смежных вершин, расположенных на одном и том же уровне иерархии ;

3. Полученный в результате граф представляется совокупностью гиперграфов ;

4. Перемножая матрицы инцидентности гиперграфов, получают матрицу W=||_ij|| размерности т^ит^с; суммируя элементы которой вычисляют значение .

21. Что такое точки сочленения и висячие вершины в графе и как они связаны со сложными системами? Приведите пример.

Висячая вершина  это вершина, которой инцидентна только одна дуга. Причем, необязательно входная или выходная дуга, важно что она единственная у этой вершины. Очевидно, что висячая вершина является либо истоком, либо стоком в графе системы. Дуга, инцидент-ная висячей вершине, называется висячей дугой.

С точки зрения анализа сложной системы, поскольку висячая вершина связана с остальными вершинами графа единственной связью, то разрыв этой связи приводит к отсоединению элемента от системы. Таким образом, надежность зависит не от надежности элемента, обозначенного висячей вершиной, а от надежности единственной связи. Поэтому проектировщик должен позаботится о дополнительных связях, повышающих надежность системы, или о повышении надежности единственной связи.

Точка сочленения -- это вершина, удаление которой из графа увеличивает число изолированных компонент графа. При удалении точки сочленения из графа нарушается достижимость отдельных вершин графа и в системе появляются обрывы цепей. Система как бы распадается на несколько несвязанных между собой подсистем, что приводит к появлению самостоятельных подсистем или изолированных элементов. Большое количество точек сочленения ухудшает надежность системы, поскольку при выходе из строя элементов, являющихся точкой сочленения, система распадается на отдельные подсистемы.