Решение:

Количество значащих нулей в двоичной записи числа  равно …

			0
			1
			2
			4

Решение: Переведем  в двоичную систему счисления: 255 : 2 =127 (ост. 1); 127 : 2 =  63 (ост. 1);   63 : 2 =  31 (ост. 1);   31 : 2 =  15 (ост. 1);   15 : 2 =    7 (ост. 1);     7 : 2 =    3 (ост. 1);     3 : 2 =    1 (ост. 1). Получили . Количество значащих нулей равно 0.

На некотором жестком диске размер кластера составляет 4096 байт. На этот диск записаны четыре файла размерами 500, 10000, 8000 и 5000 байт. Для хранения всех четырех файлов необходимо _________ кластеров(-а).

			8
			6
			7
			5,75

Решение: Кластер является наименьшей единицей адресации к данным. Когда файл записывается на диск, файловая система выделяет соответствующее количество кластеров для хранения данных файла. Например, если каждый кластер равен 512 байт, а размер сохраняемого файла составляет 800 байт, то для его хранения будут выделены два кластера. Впоследствии, если вы модифицируете файл таким образом, что он увеличится в размерах, скажем, до 1600 байт, для его сохранения будут дополнительно выделены еще два кластера. В кластер, частично занятый каким-либо файлом, нельзя поместить больше ничего. Допустим, ваш файл располагается в 10 кластерах размером по 1024 Кб, причем в последнем, десятом кластере, он занимает всего 10 байт. Что происходит с оставшимся свободным килобайтом? Ничего. Он просто пропадает для пользователя. В приведенной задаче для хранения первого файла будет отведен один кластер, так как 500 байт < 4096 байт; для хранения второго файла будет отведено 3 кластера, так как 10000 : 4096  2,44, а количество кластеров должно быть целым; для хранения третьего файла будет отведено 2 кластера, т.к. 8000 : 4096  1,95; для хранения четвертого файла будет также отведено 2 кластера, так как 5000 : 4096  1,22. Для хранения на диске всех четырех файлов необходимо: 1 + 3 + 2 + 2 = 8 кластеров.

Азбука Морзе позволяет кодировать символы для радиосвязи, задавая комбинации точек и тире. Используя код Морзе длиной не менее трех и не более четырех сигналов (точек и тире), можно закодировать _______ различных символа(-ов).

			24
			12
			128
			64

Решение: Для наборов из 3 сигналов можно закодировать  (символов). Для наборов из 4 сигналов  (символов). Всего:  (символа).

В зрительном зале две прямоугольные области зрительских кресел: одна – 6 на 12, а другая – 8 на 4. Минимальное количество бит, которое потребуется для кодирования каждого места в автоматизированной системе, равно …

			7
			2
			104
			128

Решение: Вычислим, сколько всего мест требуется закодировать: . Число, кратное двойке, превышающее 104 и ближайшее к нему – . В соответствии с формулой Хартли–Шеннона потребуется  (бит).

Для хранения неупакованного растрового изображения размером  пикселя потребовалось 512 байт памяти. Максимально возможное число цветов в палитре изображения равно …

			16
			256
			2
			4

Решение: Объем памяти V, необходимый для хранения неупакованного растрового изображения размером H x W  пикселей, в котором для хранения одного пикселя требуется С бит, определяется по формуле   Найдем С:   Число цветов N определяется по формуле Тогда

Значение суммы чисел  в восьмеричной системе счисления равно …

			320
			2110
			298
			318

Решение: Разобьем полученное число на триады: 11 010 000. 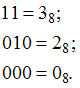Получили: 320₈.

В зрительном зале две прямоугольные области зрительских кресел: одна – 6 на 12, а другая – 8 на 4. Минимальное количество бит, которое потребуется для кодирования каждого места в автоматизированной системе, равно …

			7
			2
			104
			128

Решение: Вычислим, сколько всего мест требуется закодировать: . Число, кратное двойке, превышающее 104 и ближайшее к нему – . В соответствии с формулой Хартли–Шеннона потребуется  (бит).

Количества информации:  байт; 20000 бит; 2001 байт; 2 Кбайт, упорядоченные по убыванию, соответствуют последовательности …

			20000 бит; 2 Кбайт; 2001 байт;  байт
			байт; 20000 бит; 2001 байт; 2 Кбайт
			20000 бит;  байт; 2001 байт; 2 Кбайт
			2 Кбайт;  байт; 2001 байт; 20000 бит

Решение: Переведем все заданные величины в байты и выразим их единообразно.  байт = 1024 байт; 20000 бит =  байт = 2500 байт; 2 Кбайта =  байта = 2048 байт. Упорядочим по убыванию: 2500 байт (20000 бит); 2048 байт (2 Кбайт); 2001 байт; 1024 байт (  байт).

Аналоговый звуковой сигнал был дискретизирован сначала с использованием 65536 уровней интенсивности сигнала (качество звучания аудио-CD), а затем с использованием 256 уровней интенсивности сигнала (качество звучания радиотрансляции). Информационные объемы кодов будут различаться в ____ раз(-а).

			2
			8
			16
			256

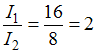Решение: По формуле Хартли–Шеннона информационный объем кода в первом случае . Информационный объем кода во втором случае . Информационные объемы кодов будут различаться в  раза.

Количество значащих нулей в двоичной записи числа  равно …

			0
			1
			2
			4

Решение: Переведем  в двоичную систему счисления: 255 : 2 =127 (ост. 1); 127 : 2 =  63 (ост. 1);   63 : 2 =  31 (ост. 1);   31 : 2 =  15 (ост. 1);   15 : 2 =    7 (ост. 1);     7 : 2 =    3 (ост. 1);     3 : 2 =    1 (ост. 1). Получили . Количество значащих нулей равно 0.

Десятичному числу  соответствует шестнадцатеричное число …

			F79D
			139716
			1397016
			ED7F

Решение: 63389 : 16 = 3961 (ост. 13₁₀=D₁₆);   3961 : 16 =   247 (ост. 9);     247 : 16 =     15 (ост. 7); 15₁₀ = F₁₆. Получили: F79D.

Двоичному числу  соответствует шестнадцатеричное число …

			5D16
			1816
			D516
			8116

Решение: Разобьем заданное число на тетрады: 0101 1101. 0101=5₁₀=5₁₆ 1101=13₁₀=D₁₆ Искомое шестнадцатеричное число – это 5D₁₆.

В кодовой таблице __________ можно закодировать 65536 различных символов.

			Unicode
			КОИ-8Р
			ASCII
			CP-1251

Решение: В кодировке Unicode один символ кодируется двумя байтами (16 бит). Всего можно закодировать  различных символов.

Бросили шестигранный игральный кубик. Количество информации в сообщении о том, какое число выпало на кубике, составляет …

			3 бит
			6 бит
			1 бит
			байт

Решение: Применим формулу для расчета количества информации , где в данном случае N – количество равновероятных событий, i – искомое количество информации (в битах). По условию задачи кубик шестигранный, следовательно, количество равновероятных событий выпадения любого числа от 1 до 6 равно: N = 6.