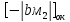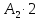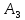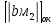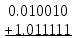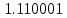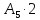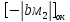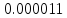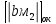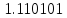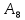ОКТ. Контрольная работа №2. Вариант 5
.docx
Задание 1.1.
Найти значения С1, С2, С3, С4, определяемые выражениями:
С1 = А+В, С2 = А-В, С3 = В- А, С4 =- А -В, где
А = 5493
В = 3275
Решение.
Представим А и В необходимо в двоично-десятичной системе:


Представим числа А и В в прямом коде :


Избавимся от операции вычитания в заданных выражениях:

Представим числа (-А) и (-В) в прямом коде :

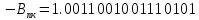
Преобразуем все переменные в дополнительный код:



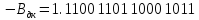
Произведем вычисления:
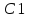 :
:
+



+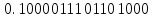


 :
:
+

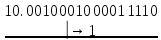

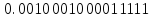
Из последней тетрады нет переноса, таким образом, это соответствует заему в нее 16 единиц (вместо необходимых 10). Следовательно, из нее необходимо удалить лишние шесть единиц, Для этого в тетраду добавляется 10 - дополнение шести до шестнадцати:
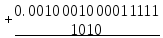



 :
:
+



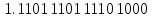


 :
:
+

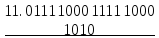

+
При образовании инверсии отрицательной тетрады в нее добавляются пятнадцать единиц. Эти 15 единиц и +1 (при формировании дополнительного кода) находятся и в сумме. А благодаря шестнадцатеричному переносу из тетрады уходит 16 единиц. Следовательно, циклический перенос 1 делать не следует.


Задание 1.2.
А {ап = -2 (порядок А), ам = + 0.56 (мантисса А)}; В{bп = 0 (порядок B), bм = -0.51 (мантисса B)}; использовать двоичный обратный код; выполнить операцию деления без восстановления остатка.
Решение.
Представим порядки и мантиссы операндов в двоичной системе счисления, сформируем модифицированные обратные коды.
 ,
,

 ,
,

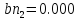 ,
,

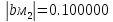 ,
,
 ,
,
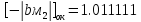
Предварительное значение порядка частного определяется следующим образом:

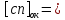

Абсолютное значение предварительное значение мантиссы частного ищется за счет выполнения 8-ми тактов (n+2 = 6+2 = 8) деления следующим образом:
|
Разряд |
Действие |
|
Значение разряда |
|
1 |
|
|
1 |
|
2 |
|
|
0 |
|
3 |
|
|
0 |
|
4 |
|
|
0 |
|
5 |
|
|
1 |
|
6 |
|
|
0 |
|
7 |
|
|
1 |
|
8 |
|
|
0 |
Получаем,
что
 .
.
Т.к. при пробном делении (разряд 1) произошло переполнение (вследствие того, что делимое по модулю больше делителя), то произведем корректировку результата. Для этого число сдвигается вправо на один разряд с добавлением единицы к порядку, равному разности порядков делимого и делителя.
Т.е.

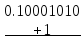

Округлим
найденное значение до 6 знаков:
 .
.
Тогда
 ,
,
 ( с учетом ранее полученного знака
частного)
( с учетом ранее полученного знака
частного)
В
десятичной системе счисления ответ
выглядит так:
 ,
,
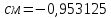 .
.