Контрольная работа 1
Задание 1
Даны комплексные
числа
,
и многочлен
.
1. Вычислить
.
2. Найти действительные
(вещественные) неизвестные x
и y
из уравнения
.
3. Решить уравнение
.
4. Разложить на линейные множители многочлен .
Решение
1. Так как для
,
то
.
Тогда
.
Умножение комплексных чисел, записанных в алгебраической форме, осуществляется по тем же правилам, что и умножение многочленов, учитывая при этом, что .
Следовательно,
.
Деление комплексных чисел, записанных в алгебраической форме, удобнее выполнять следующим образом
=
.
Следовательно,
При сложении (вычитании) комплексных чисел складываются (вычитаются) действительные и мнимые части этих чисел.
Следовательно,
.
2. Так как
,
то уравнение примет вид
.
Выделим в левой
части уравнения действительную и мнимую
части:
.
Два комплексных
выражения равны тогда и только тогда,
когда равны их действительные и мнимые
части, то есть
.
Решая систему,
находим
.
3. Так как
,
то уравнение примет вид
.
По известной формуле
.
Следовательно,
.
4. Для разложения
многочлена
на линейные множители необходимо найти
корни многочлена, то есть решить уравнение
.
Решим это биквадратное уравнение:
.
a)
;
б)
.
Следовательно,
.
Задание 2
Найти неизвестную
матрицу Х
из уравнения
Решение
Обозначим
,
,
.
Тогда уравнение
примет вид
.
Решим это матричное
уравнение:
.
Найдём
и
:
,
.
Перемножив матрицы , и , найдём неизвестную матрицу Х.
Задание 3
Найти собственные
векторы линейного оператора, заданного
в некотором базисе матрицей
Решение
Собственные
значения найдём из уравнения
Решим это уравнение:
.
Для
,
найдём
и
–
координаты первого собственного вектора
из системы уравнений
,
.
Очевидно, что
.
Полагая
,
получим первый собственный вектор
,
соответствующий первому собственному
значению
Для
,
поступаем аналогично
,
,
Полагая
,
получим второй собственный вектор
соответствующий второму собственному
значению
.
Задание 4
Дана система
линейных алгебраических уравнений
(СЛАУ)
Найти её решение:
1) методом Крамера;
2) с помощью обратной матрицы системы;
3) методом Гаусса.
Решение
1)По правилу Крамера
,
,
,
где
- определитель системы,
,
,
- вспомогательные определители. Вычислив
определители, например, по правилу
треугольников (правилу Саррюса), получим
.
Следовательно,
.
2) Матрица решений
системы
равна
,
где
-матрица
системы,
-матрица
свободных членов системы.
Найдём
.
,
где
(вычислен ранее),
-алгебраические
дополнения к элементам
матрицы
равны:
,
,
,
,
,
,
,
,
.
Таким образом,
и
.
Следовательно,
.
3) Запишем расширенную матрицу системы и, используя элементарные преобразования ( алгоритм метода Гаусса ), приведём её к ступенчатому виду
Преобразованной
матрице соответствует система
.
Из третьего
уравнения системы
.
Из второго уравнения
системы
.
Из первого уравнения системы
.
Таким образом, .
Задание 5
Даны векторы
и
.
Найти: 1)
;
2)
;
3)
;
4)
;
5)
.
Решение
Если
,
то:
1) .
Для решаемой задачи
.
2) Аналогично
.
3)
.
Для решаемой задачи
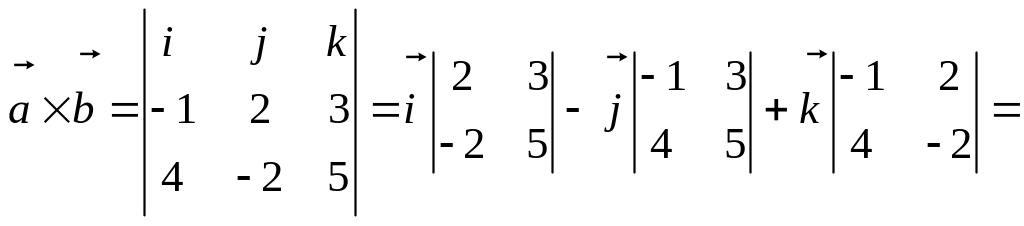
4) Аналогично
.
5)
.
Для решаемой задачи
.
Задание 6
Даны вершины
пирамиды
и точка
.
Найти:
1) длину ребра
;
2) косинус угла
между рёбрами
и
;
3) площадь грани ABC;
4) объём пирамиды;
5) уравнение прямой, на которой лежит ребро ;
6) уравнение медианы
в грани
;
7) проекцию вершины
на основание пирамиды
;
8) высоту
пирамиды;
9) записать систему линейных неравенств, определяющих пирамиду;
10) выяснить, принадлежит ли точка пирамиде ABCD.
Решение
1)Длину найдём по формуле расстояния между двумя точками
2) Угол
между рёбрами
и
будет равен углу между векторами
и
.
Введём в рассмотрение векторы и и найдём их координаты:
.
.
3) Площадь грани
ABС
(площадь треугольника АВС)
.
Введём в рассмотрение
векторы
и
и найдём их координаты:
,
.
Найдём
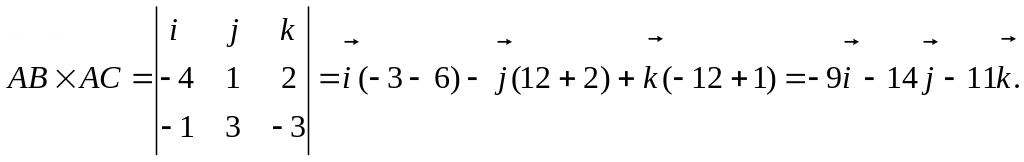
Далее
и
.
4) Объём пирамиды
.
,
,
.
Найдём
=
.
.
5) Прямая, на которой
лежит ребро АВ,
проходит через точки
и
.
Запишем уравнение этой прямой,
воспользовавшись уравнением прямой,
проходящей через две точки
и
:
.
Для решаемой задачи
или
.
6) Уравнение медианы
в грани АВС
- это уравнение прямой, проходящей через
точку
и точку
,
являющуюся серединой отрезка ВС.
Координаты точки М
найдём как координаты середины отрезка
ВС:
;
;
.
Уравнение
:
или
.
7) Проекция вершины А на основание пирамиды BCD – это точка пересечения плоскости BCD и прямой, проходящей через точку А перпендикулярно этой плоскости.
Уравнение плоскости
BCD
найдём, используя уравнение плоскости,
проходящей через три заданные точки
:
.
Для решаемой задачи
,
,
и, следовательно, уравнение АВС
,
,
,
,
.
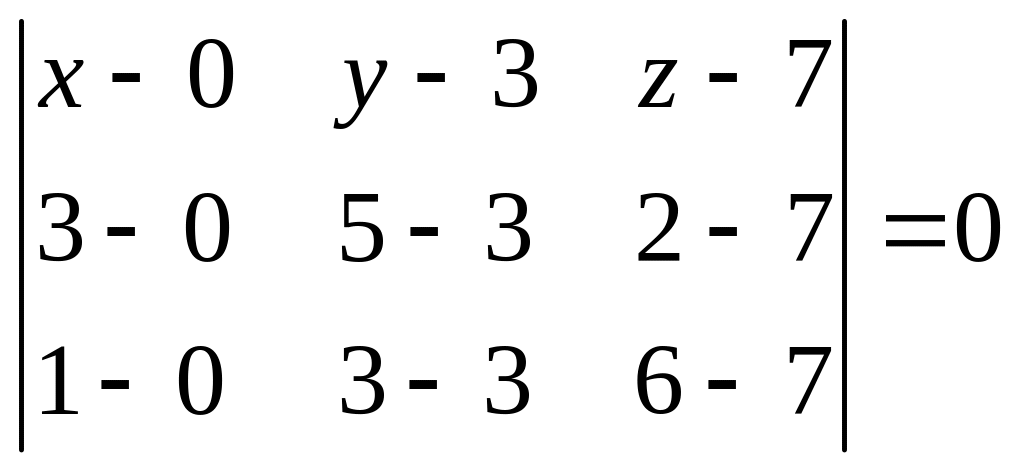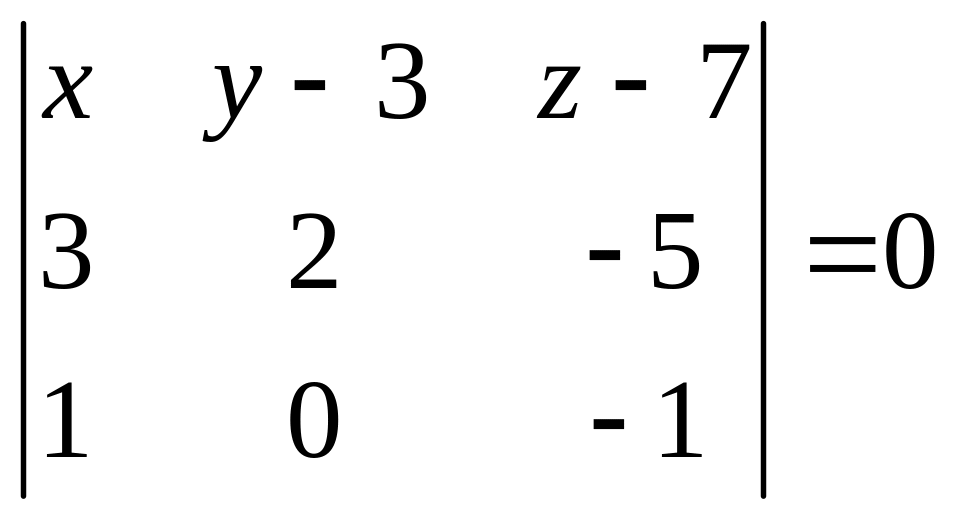Вектор
является нормальным вектором плоскости
BCD,
следовательно, этот вектор является
направляющим вектором для прямой,
проходящей через точку А
перпендикулярно плоскости ВСD.
Уравнение этой прямой
Координаты проекции точки А
на плоскость BCD
найдём из системы
или
,
,
,
,
,
,
,
.
Таким образом,
проекция точки А
на плоскость BCD
– точка
.
8) Длина высоты – это длина отрезка AN, которая равна
.
9) Найдём уравнение граней пирамиды ABC, ACD, ABD и BCD, как уравнение плоскостей, проходящих через три заданные точки
,
.
,
.
,
.
BCD:
найдено раньше
Все внутренние точки пирамиды находятся по ту сторону от плоскостей ABC, ACD, ABD и BCD что и вершины D, B, C, и А соответственно. Для вершин D, B, C и А выполняются условия
,
,
,
.
Следовательно, система линейных неравенств, определяющих пирамиду, будет
.
10) Проверим, удовлетворяют ли координаты точки системе линейных неравенств, определяющих пирамиду:
.
Второе неравенство не выполняется, следовательно, точка не принадлежит пирамиде ABCD.