
- •Рабочая программа
- •Линейная алгебра
- •Векторная алгебра и аналитическая геометрия
- •Элементы функционального анализа
- •Введение в математический анализ
- •Дифференциальное исчисление функции одной переменной
- •Интегральное исчисление функции одной переменной
- •Числовые и функциональные ряды. Гармонический анализ
- •Векторный анализ и элементы теории поля
- •Обыкновенные дифференциальные уравнения и их системы
- •Численные методы
- •Функции комплексной переменной
- •Контрольная работа 2
- •Контрольная работа 3
- •Контрольная работа 4
- •Контрольная работа 1
- •Контрольная работа 2
- •Контрольная работа 3
- •Контрольная работа 4
Векторный анализ и элементы теории поля
Литература [2], §§ 8.5-8.10, 8.13, 8.14, 8.19; [3], §§ 2.1-2.4, 3.2, 3.3, 3.8; [6], часть 1, §§ 1-8 гл.6, §§ 1, 2, 5, 6, 10 гл.9.
44. Найти область определения функции:
а)
![]() ;
б)
;
б)
![]() .
.
Указание. Учесть то, что логарифмы отрицательных чисел и нуля не существуют.
Ответ: а) Часть
плоскости, лежащая ниже параболы
![]() ;
;
б) Полосы
![]() ,
лежащие в правой
полуплоскости.
,
лежащие в правой
полуплоскости.
45. Найти линии (или
поверхности) уровня следующих скалярных
полей: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() .
.
Указание.
Линии и поверхности уровня описываются
уравнениями
![]() и
и
![]() соответственно.
соответственно.
Ответ: а)
![]() -
семейство гипербол. При
-
семейство гипербол. При
![]() -
две прямые
-
две прямые
![]() ;
б)
;
б)
![]() -концентрические
окружности, радиуса
-концентрические
окружности, радиуса
![]() ;
;
в)
![]() -
однополостные (при С>0)
и двуполостные (при С<0)
гиперболоиды вращения; при С=0-конус;
г)
-
однополостные (при С>0)
и двуполостные (при С<0)
гиперболоиды вращения; при С=0-конус;
г)
![]() -
параболоиды вращения.
-
параболоиды вращения.
46. Найти дивергенцию и ротор векторного поля:
а)
![]() ;
б)
;
б)
![]() .
.
Указание.
Дивергенция векторного поля
![]() вычисляется по формуле
вычисляется по формуле
![]() .
Ротор векторного поля вычисляется по
формуле
.
Ротор векторного поля вычисляется по
формуле
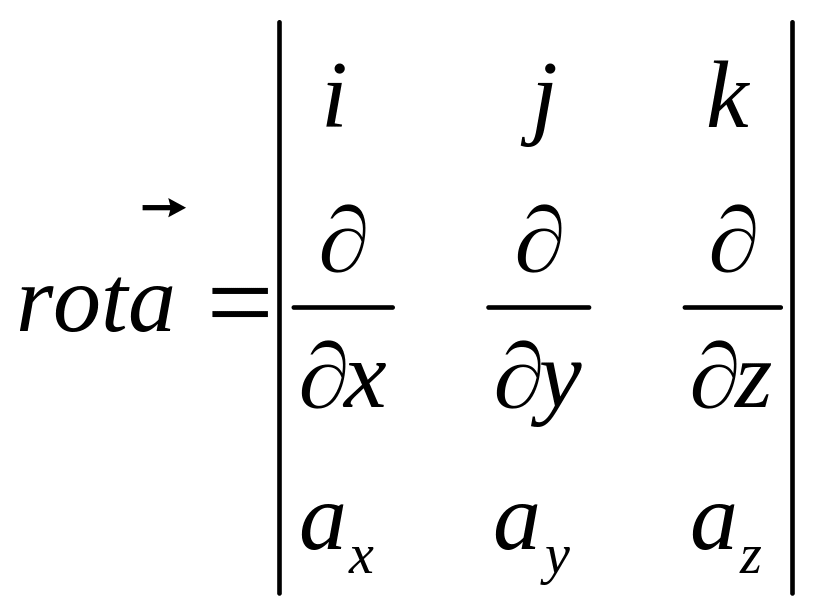 .
.
Ответ: а)
![]() ;
;
б)
![]() .
.
47.Вычислить повторные интегралы:
а)
![]() ;
б)
;
б)
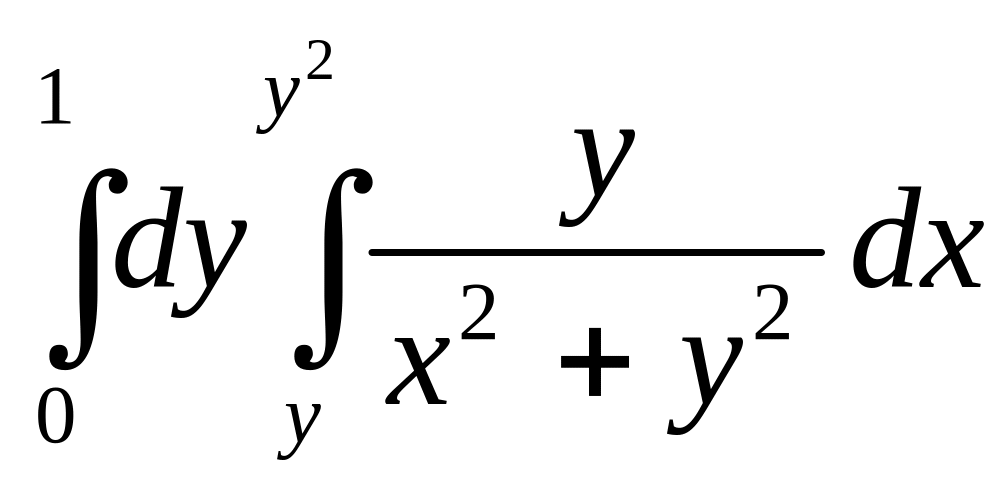 .
.
Указание. Последовательно вычислить внутренний и внешний интегралы.
Ответ: а)
![]() ;
б)
;
б)
![]() .
.
Обыкновенные дифференциальные уравнения и их системы
Литература [3], §§ 1.1-1.3, 1.21-1.23; [6], часть 1, §§ 1-4, 10, 12 гл.8.
48. Найти общее решение уравнений:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Указание. Воспользоваться методикой решения уравнений с разделяющимися переменными, однородных и линейных соответственно.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
49. Найти общее
решение уравнения: а)
![]() ;
;
б)
![]() ;
в)
;
в)
![]() .
.
Указание.
Решение линейного однородного
дифференциального уравнения с постоянными
коэффициентами
![]() ,
в зависимости от корней его
характеристического уравнения
,
в зависимости от корней его
характеристического уравнения
![]() ,
имеет вид: а) если
,
имеет вид: а) если
![]() и
и
![]() -
действительные и различные, то
-
действительные и различные, то
![]() ;
;
б) если
![]() ,
то
,
то
![]() ;
в) если
;
в) если
![]() ,
то
,
то
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() .
.
Численные методы
Литература [2], §§ 7.6-7, 9.14; [3], § 1.24; [6], часть 1, § 12 гл.4, § 20 гл.8, часть 2, гл. 7.
50. Доказать, что с
помощью рекуррентной формулы
![]() можно вычислить
можно вычислить
![]() с любой точностью. Вычислить: а)
с любой точностью. Вычислить: а)
![]() ;
б)
;
б)
![]() с точностью до
с точностью до
![]() .
.
Указание.
Убедиться, что последовательность,
заданная этой рекуррентной формулой,
сходится к
![]() ,
монотонно убывая. Выбрать за нулевое
приближение, например
,
и вычислять значения
до тех пор, пока
,
монотонно убывая. Выбрать за нулевое
приближение, например
,
и вычислять значения
до тех пор, пока
![]() ,
то есть в
,
то есть в
![]() три знака после запятой будут верные.
три знака после запятой будут верные.
Ответ: а) 1,732; б) 1,414.
51. Вычислить с
точностью до
интегралы: а)
![]() ;
б)
;
б)
![]() .
.
Указание. Разложить подынтегральную функцию в ряд и ряд почленно проинтегрировать. Учесть, что погрешность вычислений в знакочередующемся ряде не превышает по абсолютной величине первого из отброшенных членов ряда.
Ответ: а) 0;498; б) 0,480.
Функции комплексной переменной
Литература [3], §§ 6.1-6.3, 6.6, 6.10; [6], часть 2, §§ 1, 2, 6, 7 гл. 1.
52. Найти производную
функции, проверить, является ли функция
![]() аналитической: а)
аналитической: а)
![]() ;
б)
;
б)
![]() .
.
Указание.
Представить функцию в виде
![]() и проверить выполнение условий
Коши-Римана:
и проверить выполнение условий
Коши-Римана:
![]() ,
,
![]() .
Если условия Коши-Римана выполняются
в некоторой точке (области), то производную
можно найти, например, по формуле
.
Если условия Коши-Римана выполняются
в некоторой точке (области), то производную
можно найти, например, по формуле
![]() .
Если производная существует не только
в точке, но и окрестности этой точки, то
функция является аналитической в этой
точке.
.
Если производная существует не только
в точке, но и окрестности этой точки, то
функция является аналитической в этой
точке.
Ответ: а)
Производная существует только в одной
точке
![]() и
и
![]() ;
функция не является аналитической ни
в одной точке;
;
функция не является аналитической ни
в одной точке;
б) Производная
существует всюду, исключая точку
и
![]() ;
функция аналитическая всюду, исключая
точку
.
;
функция аналитическая всюду, исключая
точку
.
53. В окрестности
точки
разложить в ряд Тейлора или Лорана
функцию: а)
![]() ;
б)
;
б)
![]() .
.
Указание.
Определить особые точки функции и,
используя формулу суммы бесконечно
убывающей геометрической прогрессии,
получить требуемые разложения. Если
ряд не содержит отрицательных степеней
![]() ,
то это ряд Тейлора и он сходится в круге,
если же ряд содержит отрицательные
степени
,
то это ряд Лорана и он сходится в кольце.
,
то это ряд Тейлора и он сходится в круге,
если же ряд содержит отрицательные
степени
,
то это ряд Лорана и он сходится в кольце.
Ответ: а)
![]() ;
б)
;
б)
![]() .
.
Задания для контрольных работ
Контрольная работа 1
Задание 1
Даны комплексные
числа
![]() и многочлен
и многочлен
![]() .
.
1) Выполнить
действия:
![]() .
.
2) Найти действительные
(вещественные) неизвестные х
и у
из уравнения
![]() .
.
3) Решить уравнение
![]() .
.
4) Разложить на линейные множители многочлен .
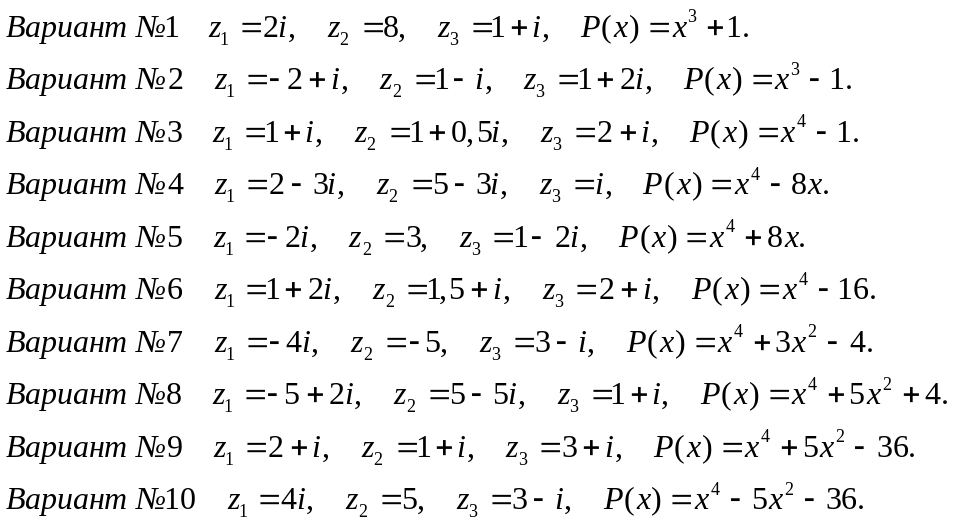
Задание 2
Найти неизвестную матрицу Х из заданного уравнения.
Вариант №1![]()
Вариант №2![]()
Вариант №3
![]()
Вариант №4![]()
Вариант №5![]()
Вариант №6![]()
Вариант №7![]()
Вариант №8![]()
Вариант №9![]()
Вариант №10![]()
Задание 3
Найти собственные значения и собственные векторы линейного оператора, заданного в некотором базисе матрицей А.
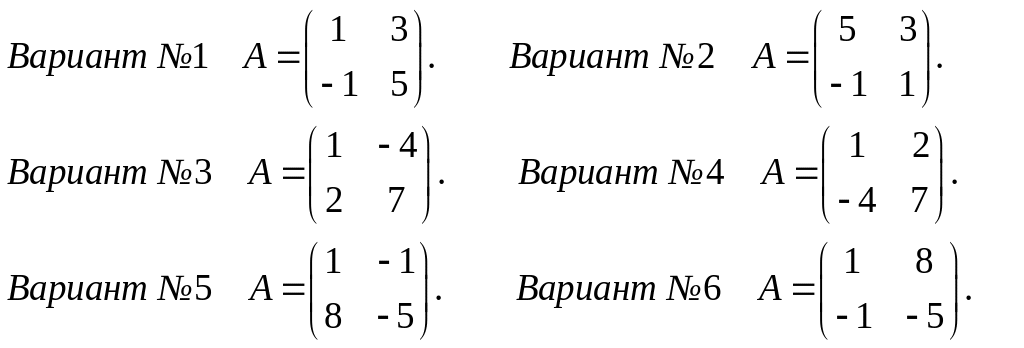
![]()
![]()
Задание 4
Найти решение СЛАУ:
1) методом Крамера;
2) с помощью обратной матрицы системы;
3) методом Гаусса.
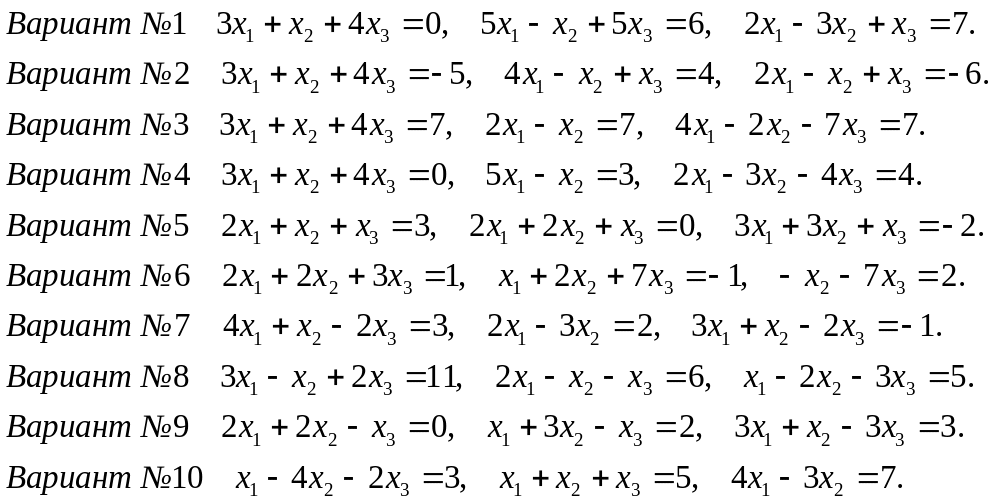
Задание 5
Даны векторы
![]() .
Найти:
.
Найти:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)![]() ;
5)
;
5)![]() .
.
Вариант №1![]()
Вариант №2
![]()
Вариант №3
![]()
Вариант №4
![]()
Вариант №5
![]()
Вариант №6
![]()
Вариант №7
![]()
Вариант №8
![]()
Вариант №9
![]()
Вариант №10![]()
Задание 6
Даны вершины
пирамиды ABCD
и точка
![]() .
Найти:
.
Найти:
длину ребра АВ;
косинус угла между ребрами АВ и СD;
площадь грани АВС;
объем пирамиды;
уравнение прямой, на которой лежит ребро АВ;
уравнение медианы
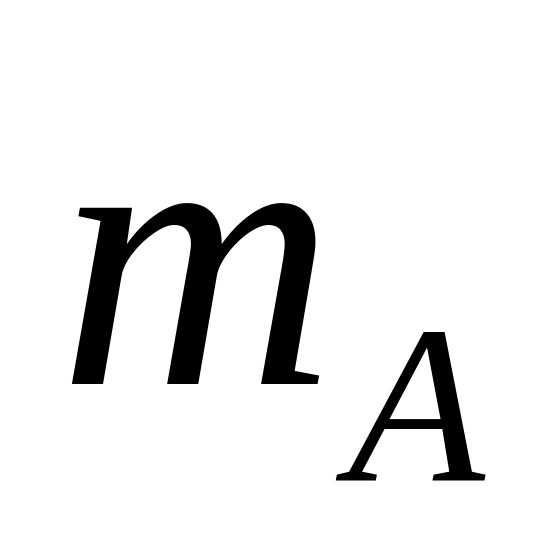 в грани АВС;
в грани АВС;проекцию вершины А на основание пирамиды ВСD;
высоту
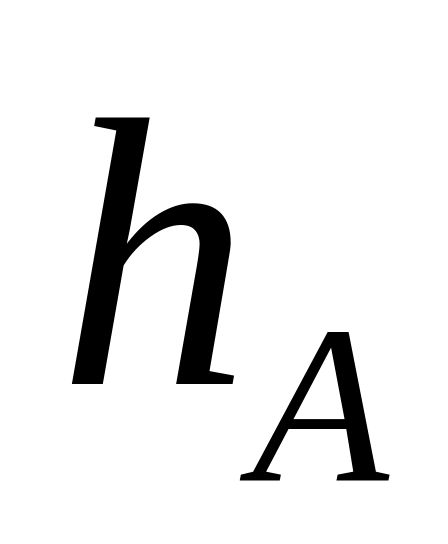 пирамиды;
пирамиды;записать систему линейных неравенств, определяющих пирамиду;
выяснить, принадлежит ли точка
 пирамиде АВСD.
пирамиде АВСD.

