Контрольная работа 4

Задание 1

В таблице приведены пять экспериментальных значений искомой функции . Аппроксимировать эту функцию линейной функцией методом наименьших квадратов. Построить график аппроксимирующей функции и экспериментальные точки.

x	1	2	3	4	5
y	1,8	1,3	3,3	4,8	3,8

Решение

Параметры а и b, для которых осуществляется наилучшее приближение (по методу наименьших квадратов), определяются из системы уравнений

Для получения системы, соответствующей заданным значениям, можно рекомендовать оформлять вычисления в виде таблицы

	xi	yi	xi2	xiyi
1	1	1,8	1	1,8
2	2	1,3	4	2,6
3	3	3,3	9	9,9
4	4	4,8	16	19,2
5	5	3,8	25	19
	15	15	55	52,5

Составляем систему уравнений .

Решая систему, находим , .

Таким образом, .

Делаем чертёж

Задание 2

Изменить порядок интегрирования в повторном интеграле . Изобразить область интегрирования.

Решение

Пределы интегрирования в повторном интеграле зависят от уравнений границ области интегрирования. Следовательно, область интегрирования ограничена линиями , , , . Построим область интегрирования

При изменённом порядке интегрирования область интегрирования необходимо разбить на две части, так как при любом фиксированном верхняя граница области определяется разными уравнениями.

Следовательно, .

Задание 3

С помощью тройного интеграла вычислить объём тела, ограниченного координатными плоскостями и плоскостью . Изобразить данное тело и его проекцию на плоскость .

Решение

Если , то где V-объём области интегрирования.

Изобразим данное тело и его проекцию на плоскости .

.

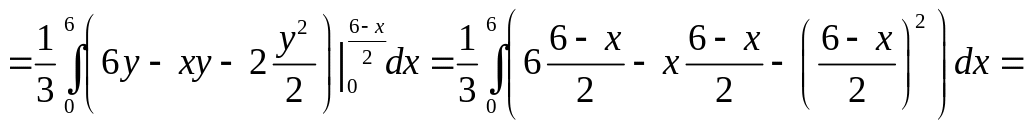
Задание 4

Найти общее решение дифференциального уравнения .

Решение

Данное уравнение является линейным дифференциальным уравнением первого порядка. Применим для его решения метод подстановки: .

Заданное уравнение примет вид: или .

Функцию V найдём из уравнения .

Решим это уравнение .

Функцию U найдём из уравнения , то есть из уравнения .

Решим это уравнение:

.

Общее решение заданного уравнения .

Задание 5

Найти четыре первых, отличных от нуля, члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Решение

Будем искать решение уравнения в виде ряда

.

По условию и .

Продифференцировав обе части данного дифференциального уравнения, получим . Найдём .

Продолжим этот процесс

.

Следовательно .

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами .

Требуется:

1) найти общее решение системы;

2) записать систему и её решение в матричном виде.

Решение

1) Найдём общее решение системы, сведя её к дифференциальному уравнению второго порядка.

Для этого: продифференцируем первое уравнение системы: ; подставим в него значение из второго уравнения: .

Составим систему , выразим из первого уравнения и подставим во второе: или .

Составим характеристическое уравнение и найдём его корни: .

Следовательно, .

Так как , то .

Таким образом, .

2) Если ввести в рассмотрение матрицы и , то система будет иметь вид , а её общее решение .

Литература

1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. М.:Наука, 1980.

2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. М.:Наука, 1998.

3. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М.:Наука, 1981.

4. Высшая математика для экономистов. Под ред. Кремера Н. Ш., М.: ЮНИТИ, 1998.

5. Калесников А. Н. Краткий курс математики для экономистов. М.:ИНФРА-М, 1997.

6. Сухинов А.И., Фирсов И.П., Цирулик В.Г. Конспект лекций по курсу высшей математики, часть 1,2, Таганрог, 2004.

7. Сборник заданий к типовым расчетам и контрольным работам по математическим дисциплинам, часть 1, Таганрог, 2003.

8. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах, части 1-3,Высшая школа,

М.,1971.