Переход к базису или-не
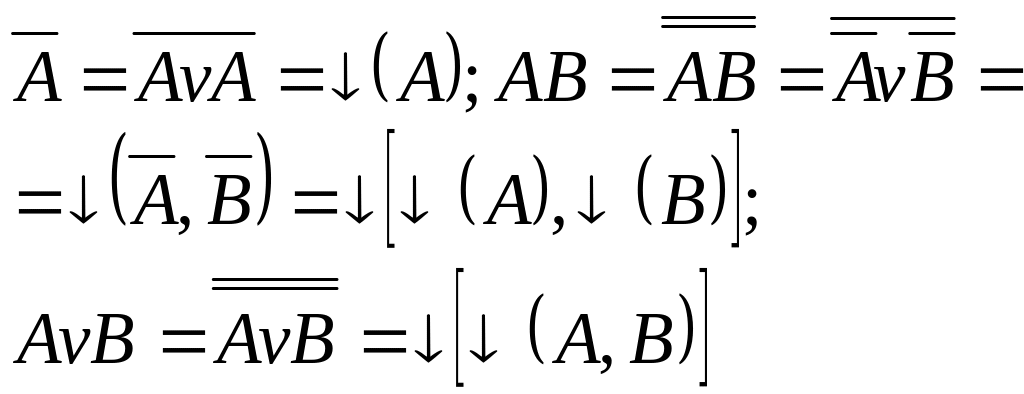
Правила перехода: инверсия реализуется подачей аргумента на элемент ИЛИ-НЕ; конъюнкция получается инвертированием аргументов с последующей подачей их на элемент ИЛИ-НЕ; дизъюнкция выполняется подачей аргументов на элемент ИЛИ-НЕ с последующей инверсией.
В общем случае на свободные входа элементы ИЛИ-НЕ должны быть подана либо константы 0 , либо подключены уже используемые в элементе входные сигналы. В лабораторном макете сигналы на свободных входах элементов ИЛИ-НЕ соответствуют константе 0 , поэтому эти входы можно оставить незадействованными (на схемах свободные входы можно не показывать).
Преобразуем МДНФ и МКНФ функции рис.12,б.
МДНФ:
В соответствующей схеме (рис.15,а) r = 3, S = 10.
МКНФ:
В соответствующей схеме (рис.15,б) r = 2, S = II. Как видно, реализация на элементах ИЛИ-НЕ МДНФ функции приводит к трехуровневой схеме, реализация МКНФ - к двухуровневой схеме.
Рис.15
Из четырех схем, реализующих функцию рис.12,б .предпочтителен вариант на рис.14, а ( г = 2, S = 9). Если же в КС необходимо использовать элементы ИЛИ-НЕ и допускается использование трехуровневой схемы, то следует выбрать вариант на рис.15, а. (г = 3, S= 10), и т.д. В общем случае выбирается вариант КС, который при заданных значениях J и F является оптимальным в смысле минимума используемого в схеме оборудования при выполнении ограничений на быстродействие КС.
Следует также иметь в виду, что синтезируемые схемы часто можно дополнительно упростить, применяя скобочные формы представления функций [3]. Скобочные формы в булевом базисе получают путем вынесения за скобки общих частей нескольких произведений (в ДНФ) или нескольких дизъюнкций (в КНФ). Так, например, получим скобочную форму из МДНФ функции рис.12, а. :
.
Переведем МДНФ и скобочную форму в базис И-НЕ.
Скобочная форма:
Схемы, реализующие МДНФ ( r = 2, S = 9) и скобочную форму ( r = 3, S = 8), приведены на рис.16. Схема рис.16, б не только проще, но и требует лишь двухвходовых элементов. Но в любом случае скобочные формы приводят к увеличению числа уровней r в схеме.
На практике к скобочным формам прибегают, наряду с разделением входов, для получения схем, удовлетворяющих требуемому
Рис.16
значению коэффициента J[3]. При этом разделение входов используется в последнюю очередь, либо сопровождается увеличением числа входов S в КС.
Синтез кс со многими выходами
Задачу синтеза схемы с m выходами, работа которой описывается системой из т функций, можно свести к задаче синтеза КС с одним выходом, если каждую из функций реализовать отдельно. При этом получаем искомую схему с т выходами, состоящую из т независимых КС. Однако в общем случае схему можно существенно упростить, объединив участки схемы, реализующие одинаковые выражения в уравнениях нескольких функций.
Общая идея минимизации схем со многими выходами сводится к получению таких выражений для совокупности переключательных функций, в которых оптимально используются члены, общие для нескольких функций [I].
Рис.17
Пусть, например,
требуется построить двухуровневую КС,
реализующую на элементах булевого
базиса систему трех функций, заданных
в ДНФ. Диаграммы Вейча функций представлены
на рис.17. При раздельной минимизации
можно получить следующие МДНФ функций:
.
Схема, построенная по этим выражениям,
будет содержать 24 входа элементов (S =
24). В то же время можно построить искомую
схему с S
= 21, если согласно рис.18 представить
функции в виде следующих ДНФ:
При этом
предполагается, что любой из дизъюнктивных
членов
,
повторяющихся в выражениях для нескольких
функций, будет реализовываться одним
элементом, общим для этих функций.
Рис.18
Синтез схем с многими выходами, оптимальных по количеству оборудования, связан с практически неосуществимым перебором большого числа вариантов схемы. Известные методы синтеза [l,3] позволяют сократить перебор, однако при этом получаются не оптимальные, а только в той или иной степени близкие к ним схемы.
Содержание отчета
1. Представление реализуемых ПФ таблицами истинности и диаграммами Вейча.
2. Получение минимальных нормальных форы ПФ.
3. Переход к базисам И-НЕ и ИЛИ-HЕ.
4. Функциональные схемы на элементах И-НЕ и ИЛИ-НЕ