
Задачник по аэрогидромеханике
.pdf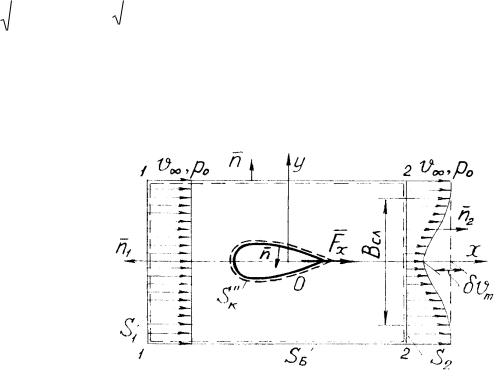
Для вычисления по (7.11) неизвестным является давление p2 |
во втором |
|||||||||||||||||||||||||||||||||||||||||
сечении. Не рассматривая |
|
наружное обтекание корпуса судна, давление p2 |
||||||||||||||||||||||||||||||||||||||||
будем искать по уравнению Бернулли |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
p |
|
|
|
1 |
v 2 |
|
|
p |
|
|
|
|
|
2 |
v 2 |
|
v 2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1ср |
|
|
2 |
|
|
|
|
2ср |
|
1ср |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
(7.12) |
||||
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2g |
|
|
g |
|
|
|
|
2g |
|
2g |
|
|
|
|||||||||||||||||||
где принято z1 z2 по условию задачи. Из (7.12) получим |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
v 2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
p |
|
p |
|
1ср |
( |
|
|
) |
2ср |
|
|
. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вычислим |
значения |
|
|
необходимых |
|
тригонометрических |
функций: |
|||||||||||||||||||||||||||||||||||
cos cos 45o |
0,707; |
|
sin sin 45o 0,707; |
cos cos15o 0,259; |
||||||||||||||||||||||||||||||||||||||
sin sin 75o |
0,966; |
|
cos( ) cos( 75o |
45o ) 0,866. |
|
|||||||||||||||||||||||||||||||||||||
Подстановка числовых значений в полученные формулы приводит к |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
v1ср |
1,0 / 1,0 1,0 м / с, |
|
|
|
|
v2ср |
|
|
1,0 / 1,2 0,866 0,96 м / с , |
|
||||||||||||||||||||||||||||
|
|
|
|
10 103 |
103 1,0 2 |
|
|
|
|
|
|
|
|
|
|
103 0,96 |
2 |
1,25 7,67 103 Па , |
||||||||||||||||||||||||
|
p |
2 |
|
|
|
|
|
|
|
|
(1,10 4,6) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
F |
|
103 |
1,05 1,0 2 1,0 103 |
1,10 0,96 2 1,2 0,707 0,866 10 103 |
1,0 |
|||||||||||||||||||||||||||||||||||||
жх |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7,67 103 |
0,259 1,2 |
7,92 103 Н, |
|
|
|||||||||||||||||||||||||||||
F |
103 |
1,10 0,96 2 |
0,707 0,866 1,2 7,67 103 |
1,2 0,966 9,64 103 Н. |
||||||||||||||||||||||||||||||||||||||
жy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полное усилие, испытываемое стенками канала, |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
F |
F 2 F 2 |
|
|
7,922 9,642 103 12,5 103 Н. |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
ж |
жх |
|
|
жy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задача 7.2.2. Определить сопротивление симметричного крыла по расчетам измерения профиля скорости за ним в сечении 2-2 следа (рис.7.5), где дав-
ление p0 |
постоянно и равно давлению в потоке перед крылом. Профиль скоро- |
||||||
сти в следе аппроксимируется выражением |
|||||||
|
v |
m |
|
|
|
2 y |
|
v v |
|
|
|
cos |
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
. |
||
|
2 |
|
|
|
Bсл |
||
Скорость |
набегающего |
||||||
воздушного |
|
( 1,23кг / м3 ) |
|||||
потока v 50 м / с , |
макси- |
||||||
мальный |
дефицит скорости |
||||||
на оси следа |
|
vm 20 м / с , |
|||||
ширина следа |
|
Bсл 0,2 м . |
|||||
Дано: 1,23кг / м3 ; |
|||||||
v 50 м / с; vm 20 м / с; В |
|||||||
Определить: Fх |
|
Рис. 7.5 |
|||||
101
Решение. Крыло считаем длинным, обтекание – плоским параллельно Oxy. Будем вычислять сопротивление для единичной длины крыла. Проводим контрольную поверхность, состоящую, как показано штриховыми линиями на
рис. 7.5, из двух частей. Первая часть S включает два отдаленных от профиля
к
одинаковых по площади сечения потока 1-1 (S ) и 2-2 (S ) и две боковые по-
верхности 1-2 ( Sб ), также удаленные от профиля. Вторая часть |
|
контроль- |
|||
Sк |
|||||
ной поверхности совпадает с профилем. |
|
|
|
|
|
На внешней части контрольной поверхности |
действуют только нор- |
||||
Sк |
|||||
мальные гидродинамические давления, поскольку силы трения (касательные напряжения) проявляются лишь в непосредственной близости к поверхности
обтекаемого тела (в пограничном слое). Так как контрольная поверхность S
к
проведена на большом удалении от тела, давления во всех ее точках равны давлению в невозмущенном потоке p . Интеграл постоянных давлений в (7.2) по
замкнутой поверхности в проекции на любую ось равен нулю.
По условиям двухмерности и симметричности течения относительно оси х силовое воздействие на профиль сводится к силе, направленной вдоль оси x, которая определяется согласно (7.3) формулой
|
Fx |
vn vx dS . |
|
|
(7.13) |
|
|
|
S |
|
|
|
|
|
|
к |
|
|
|
|
Вычислим поток количества движения в виде |
|
|
|
|||
vn vx dS vn vx dS vn vx dS vn vx dS . |
||||||
S |
S |
S |
2 |
S |
б |
|
к |
1 |
|
|
|
||
В сечении 1-1 vn v , vx v ; в сечении 2-2 |
vn v, |
vx v ; на боковой |
||||
поверхности можно считать |
vx |
v , а проекция скорости на внешнюю нор- |
||||
маль непосредственно условиями задачи не определена. Следует заметить, что
через поверхность |
Sб жидкость перетекает благодаря оттеснению потока воз- |
|||||
никшим у профиля пограничным слоем. С учетом сделанных замечаний |
|
|||||
vn vx dS v 2 dS v22 dS v vn dS . |
(7.14) |
|||||
S |
S |
S |
2 |
S |
б |
|
к |
1 |
|
|
|
||
Расход через сечение S |
из-за дефекта скорости меньше, чем через |
S . |
||||
Напишем условие неразрывности для рассматриваемого объема жидкости внутри контрольной поверхности, полагая ее несжимаемой,
|
|
v dS |
vdS |
vn dS 0 , |
|
|
|
S1 |
S2 |
Sб |
|
откуда |
|
|
|
|
|
vn dS v dS vdS ( v v )dS , |
( S1 S2 ) . |
||||
Sб |
S1 |
S2 |
S1 |
|
|
Подставив полученное выражение в уравнение (7.14) получим |
|||||
vn vx dS ( v 2 v 2 v 2 v v )dS v( v v )dS . |
|||||
S |
S |
|
|
S |
|
к |
|
1 |
|
|
1 |
102
Для вычисления сопротивления крыла, т.е. силы, приложенной к движущемуся крылу со стороны жидкости в проекции на направление, противоположное скорости его движения, по (7.13) будем иметь
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
v |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
F |
|
|
|
|
v(v v |
|
|
|
)dS v |
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.15) |
||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
v |
|
|
|
|
v |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
v |
m |
|
|
|
|
|
|
|
|
|
|
2 y |
|
|
|
|
||||||||
В рассматриваемой задаче |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Так как сопротив- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 cos |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
2v |
|
|
|
|
|
|
|
|
Bсл |
|
|
|
|
|||||||||||
ление ищем для единичного элемента, то |
|
dS dy . При этом интегрирование |
|||||||||||||||||||||||||||||||||||||||||||||
по площади в (7.15) заменяем на интегрирование по ширине следа Bсл : |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Bсл |
/ 2 |
|
|
v |
|
|
|
|
|
|
|
|
|
2 y |
|
v |
|
|
|
|
|
|
|
2 y |
|
||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
m |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Fx 2 v |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
dy |
|
||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
2v |
|
|
|
|
Bсл |
2v |
|
|
|
|
Bсл |
|
|||||||||||||||||||||||
|
|
|
|
B |
сл |
|
|
|
|
3 |
|
|
v |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
v vm |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
4 |
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Подстановка числовых данных задачи дает |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
3 |
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Rx |
1,23 50 20 |
|
|
1 |
|
|
|
|
|
|
|
|
|
86,1 Н . |
|
|||||||||||||||||||||||||||||
|
|
|
|
2 |
4 |
50 |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
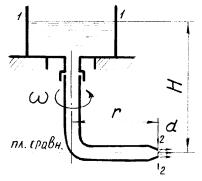
Задача 7.2.3. |
|
Вода вытекает из неподвижного сосуда через вращающую- |
|||||||||||||||||||||||||||||||||||||||||||||
ся трубку с насадком диаметром |
|
|
|
d=20 мм |
|
|
под статическим напором |
H=1,2м |
|||||||||||||||||||||||||||||||||||||||
(рис. 7.6). Радиус вращения выходного сечения насадка |
r=500 мм.. Определить |
||||||||||||||||||||||||||||||||||||||||||||||
расход через трубку и внешний момент М, который должен быть к ней приложен при частоте вращения n=200 об/мин. Гидравлическими и механическими
сопротивлениями пренебречь. |
|
|
|
|
||
Дано: H=1,2 м; |
r=500 мм=0,5 м; |
|
|
|
||
n=200 об/мин=3,33 об/с. |
|
|
|
|
||
Определить: Q; |
M ж . |
|
|
|
|
|
Решение. 1. Расход воды через трубку найдем |
||||||
из уравнения неразрывности |
Q w2 S2 , где |
w2 |
- |
|||
относительная скорость движения воды при выходе |
||||||
из трубки. Для определения w2 |
используем уравне- |
|||||
ние Бернулли для |
относительного |
движения жид- |
||||
кости в равномерно |
вращающемся |
канале |
(7.9), |
Рис. 7.6 |
||
которое для сечений 1-1 и 2-2 относительно плоскости сравнения, проходящей по оси насадка, будет иметь вид
H |
w22 |
|
u22 |
. |
(7.16) |
|
|
||||
|
2g |
|
2g |
|
|
Здесь p p , так как на свободной поверхности 1-1 и в выходном сечении струи 2-2 давление атмосферное. На свободной поверхности 1-1 также w1 0 и u . Гидравлическими потерями по условию задачи пренебрегаем.
103

Переносная скорость u определяется через угловую скорость вращения
трубки из выражения
u2 r 2 nr 2 3,14 200 0,50 10,47 м / с.
Из (7.16) имеем
w |
2gH u 2 |
|
2 9,81 1,2 10,472 11,5 м / с . |
2 |
2 |
|
|
Тогда расход
Q 11,5 3,14 0,022 3,62 10 3 м3 / с . 4
2. Внешний момент М, равный динамическому реактивному моменту
стенки трубки на поток; относительно оси вращения, согласно (7.8), будет
M Q r vu2 ,
где vu2 - окружная составляющая абсолютной скорости потока на выходе из
трубки.
Так как относительная скорость истечения воды из трубки совпадает с осью насадка, т.е. с радиусом вращения, то окружная составляющая vu2 абсо-
лютной скорости потока на выходе будет совпадать с переносной скоростью выходного сечения 2-2 vu2 = u .
Таким образом имеем
MQ r u2 103 3,62 10 3 0,5 10,47 19,0 Н м .
7.3.З а д а ч и
7-1 2. Найти упор P и коэффициент полезного действия (КПД) водо-
метного движителя. Продольная составляющая скорости vx |
во входном сече- |
нии приемного патрубка площадью S во всех точках равна |
кv . Изменением |
обтекания корпуса за счет работы движителя пренебречь. Коэффициенты, ха-
рактеризующие скорости в выходном сечении сопла - |
и |
, |
во входном |
|||||||||
сечении - и |
, коэффициент потерь напора внутреннего тракта, отнесен- |
|||||||||||
ный к средней скорости на выходе, , |
площадь выходного сечения сопла |
|||||||||||
S , S , скорость набегающего потока |
v , средняя скорость выброса воды |
|||||||||||
v |
в |
. Вычислить |
P и при |
к 0,7; 1,0; S 0,2 м2 ; |
|
|
=1,25; |
|
=1,1; |
|||
|
|
|
|
1 |
|
|
|
|
|
|||
=1,1; =1,05. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Указание. Под КПД водо- |
|||||||
|
|
|
|
|
метного движителя следует по- |
|||||||
|
|
|
|
|
нимать отношение его полезной |
|||||||
|
|
|
|
|
мощности Pv к гидравлической |
|||||||
|
|
|
|
|
мощности, |
которую |
сообщает |
|||||
|
|
|
|
|
движитель - Q gH . |
|
|
|
||||
К задачам 7-1 2
104
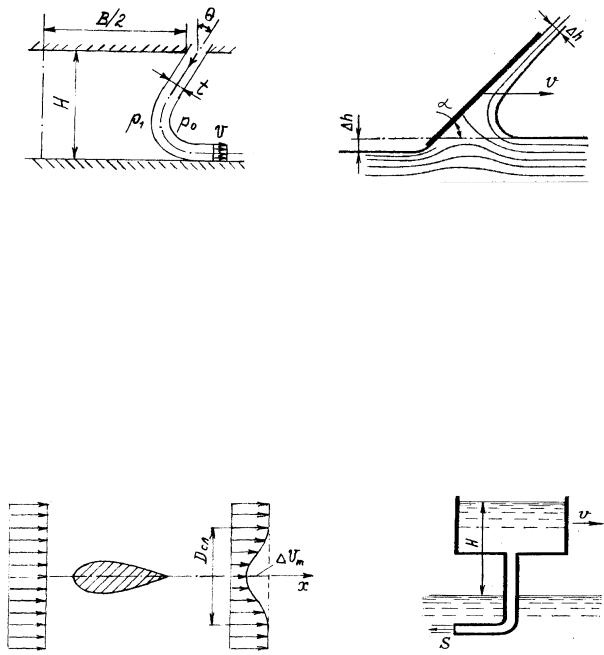
7-3 4. Найти поддерживающую силу P на единицу длины схематизированного аппарата на воздушной подушке. Вязкостью воздуха пренебречь, толщину струи считать малой по сравнению с высотой парения H, скорость в струе v, давления на внешней p и внутренней p ее поверхностях считать посто-
янными, угол наклона сопла по отношению к вертикали . Найти общее выражение P и ее значение при 20о , B 3,2 м, t 0,05 м, 1,23 кг / м3 .
.
7-5 6. Пластина, наклоненная к горизонту на угол , глиссирует по поверхности неподвижной воды со скоростью v, вызывая за собой понижение уровня на h =10 мм. Пренебрегая вязкостью жидкости и силой тяжести и рассматривая поток как плоский, определить в расчете на единицу ширины пластины гидродинамическую реакцию потока, а также мощность, необходимую для перемещения пластины.
К задачам 7-3 4 К задачам 7-5 6
7-7 8. Определить сопротивление Rтк тела вращения при осесиммет-
ричном обтекании водой по измерению скорости в сечении следа, где давление p0 постоянно и равно давлению в потоке перед телом. Полученный профиль
скорости выражается приближенной формулой v= v - vm [1+cos(2 r/ Dсл )], где r – расстояние от оси до рассматриваемой точки, Dсл - диаметр следа. Вычислить Rтx при Dсл =1,0 м.
7-9 10. Определить реакцию и полезную механическую мощность, развиваемую потоком воды на подвижном сосуде, который перемещается со скоростью v и из которого жидкость вытекает через трубу с выходным сечением
S=25 см2 под постоянным напором H. Гидравлическими сопротивлениями пренебречь.
К задачам 7-7 8 |
К задачам 7-9 10 |
v , p0 |
, p0 |
105

7-11 12. Водометный движитель судна создает тяговую силу за счет струи воды, забираемой насосом спереди судна и выбрасываемой в корме с относительной скоростью w. Определить силу тяги, создаваемую движителем и развиваемую им мощность, пренебрегая гидравлическими сопротивле-
К задачам 7-11 12 ниями в подводящей и отводящей трубах. Скорость судна v, подача насоса Q=750 л/с.
7-13 14. Пластина, введенная в свободную струю воды перпендикулярно ее оси, отсекает часть расхода струи Q1 и вызывает отклонение остальной час-
ти струи на угол . Определить силу воздействия струи на пластину и угол отклонения , если скорость струи v, полный расход Q=36 л/с. Весомостью жидкости и трением струи о пластину пренебречь.
7-15 16. Пластина, введенная в свободную струю воды перпендикулярно ее оси, отклоняет часть расхода струи на угол . Определить силу воздействия струи на пластину, если скорость струи v при полном расходе Q=32 л/с. Весомостью жидкости и трением струи о пластину пренебречь.
7-17 18. Определить проекции равнодействующей гидродинамических сил, действующих на единицу длины крылового профиля в бесконечной пло-
ской решетке, имеющей шаг a. Жидкость – невязкая ( 1,23 кг / м3 ), поток –
установившийся. Скорость перед решеткой v |
|
v |
и составляет угол |
1 |
45o |
|||
|
|
1 |
|
|
|
|
||
с осью O , скорость за решеткой - v |
2 |
и угол |
|
|
2 |
15o . Принять давления пе- |
||
|
|
|
|
|
|
|
||
ред и за решеткой одинаковыми. |
|
|
|
|
|
|
|
|
К задачам 7-13 16 |
|
|
К задачам 7-17 18 |
|
|
|||
106
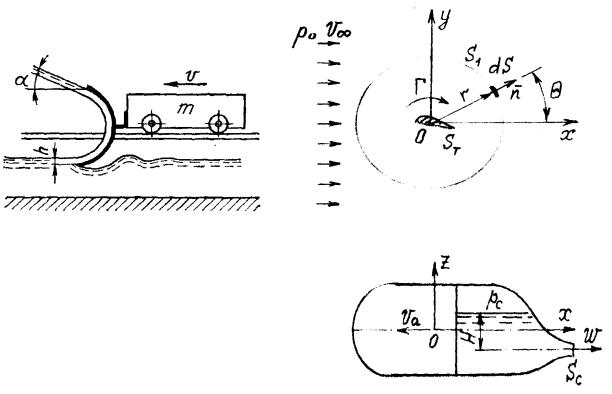
7-19 20. Для быстрого торможения тележки опытного стенда в канал с водой опускается цилиндрический ковш, который отбрасывает струю воды в сторону движения тележки под углом к горизонту (на схеме изображено относительное обтекание ковша). Определить толщину h струи, которую должен захватить ковш, чтобы тележке массой 200 кг, имеющей начальную скорость v сообщить начальное замедление a=-10g. Ширина ковша B=20 см. Силой тяжести струи и потерями напора при обтекании ею ковша пренебречь. С какой силой при этом струя будет прижимать тележку к рельсам ?
7-21 22. Определить равнодействующую гидродинамических сил на единицу длины крылового профиля, вокруг которого создана циркуляция Г. Профиль обтекается установившимся потоком идеальной жидкости
( 1,23 кг / м3 ), имеющим скорость v v .
Указания. 1 Циркуляцию представить бесконечной вихревой нитью по оси Oz. 2.Давления p0 и p на бесконечности и на контрольной поверхности S1 связа-
ны интегралом Эйлера, откуда определяется избыточное гидродинамическое давление p- p0 на S1.
К задачам 7-19 20 К задачам 7-21 22
7-23 24. Найти тягу Rт , создаваемую |
|
гидрореактивным движителем схематизиро- |
|
ванного подводного аппарата. Скорость |
|
движения аппарата va постоянна, площадь |
|
выходного сечения сопла движителя Sс , ко- |
|
эффициент потери напора в нем , распре- |
|
деление скорости в выходном сечении сопла |
|
принять постоянным; избыточное давление |
К задачам 7-23 26 |
на поверхности воды в цистерне движителя |
|
pс и ее уровень Н считать постоянными. |
Вычислить Rт при vа v м/с, |
Sс =0,0028 м 2 , pс =1,0 МПа, =0,1, если погружение оси сопла под свободную поверхность составляет 8,0 м.
107
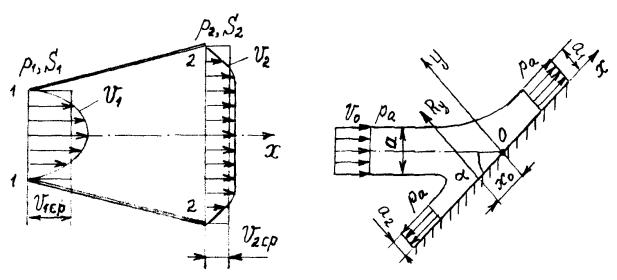
7-25 26. Какое давление pс следует создать на поверхности воды в цис-
терне схематизированного подводного аппарата, чтобы получить гидрореактивным движителем тягу Rт = 2,0 кН, если диаметр выходного сечения сопла
движителя d, а ось погружена под свободную поверхность на 10 м. Скорость движения аппарата и уровень воды в цистерне принять постоянными и равными соответственно vа v м/с и H=1,0 м. Потерями при движении воды в со-
пле пренебречь.
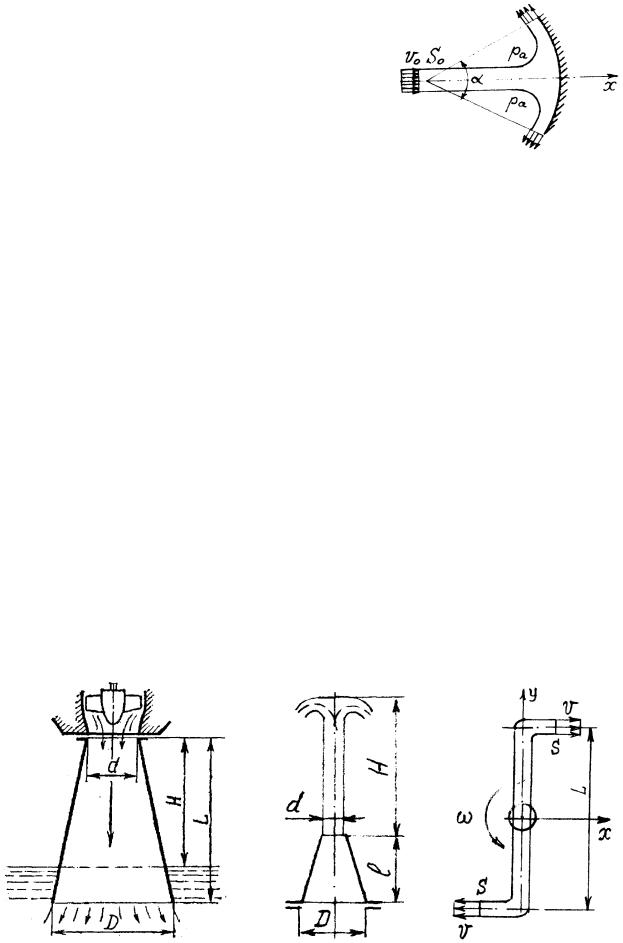
7-27 28. Найти равнодействующую гидродинамических сил на стенки диффузора, симметричного относительно оси x, если во входном сечении средняя скорость v1ср v и давление p1 p . Профили скоростей в сечениях
1-1 и 2-2характеризуется коэффициентами неравномерности кинетической энергии 1 1,10; 2 1,25 и количества движения 1 1,03; 2 1,10 . Пло-
щади сечений S1 0,5S2 0,1м2 , коэффициент потерь, отнесенный к скорости в сечении 1-1, =0,2.
7-29 30. Найти общее выражение величины и точку приложения равнодействующей избыточного гидродинамического давления на единицу ширины при косом ударе плоской струи о неподвижную плоскость и вычислить их значение для воды при a=0,1 м, v0 v и угле . Потерями энергии при течении
жидкости вдоль плоскости пренебречь, профили скорости в удаленных сечениях струи считать равномерными.
К задачам 7-27 28 К задачам 7-29 30
108
7-31 32. Найти общее выражение силы избыточного гидродинамического давления, вызываемой струей воды, направленной вдоль оси симметрии на неподвижную криволинейную по-
верхность. |
Вычислить |
ее значение при |
||||
S |
0 |
0,06 м 2 |
, v |
0 |
v и угле |
, потерями энергии |
|
|
|
|
|
||
вдоль струи пренебречь, профили скорости в удаленных сечениях струи считать равномерными.
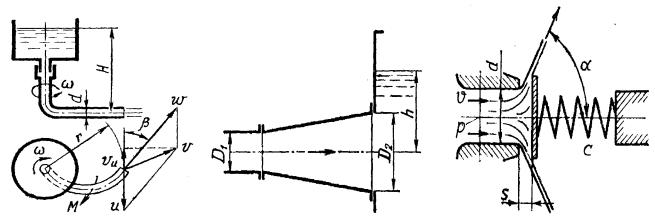
К задачам 7-31 32 7-33 34. Отсасывающая труба гидротурбины выполнена в виде верти-
кального тонкостенного конического диффузора с диаметрами d=1.0 м, D=2,0м и длиной L=4 м. Входное сечение трубы расположено на Н м выше уровня воды, скорость в этом сечении v1 v , коэффициент потерь в диффузоре =0,25.
Определить гидравлическую осевую силу, действующую на трубу, полагая, что давление на стенки погруженной под уровень части трубы равно гидростатическому.
7-35 36. Фонтан бьет на высоту Н, вытекая из сопла, имеющего форму конусного конфузора с диаметрами D=120 мм и d=50 мм и длиной l=0.40 м. Вычислить усилия на болтовую систему, пренебрегая потерями при движении воды в сопле. Распределения скоростей по сечениям сопла считать равномерными.
7-37 38. Найти момент гидродинамических сил, возникающих при вытекании воды из двух противоположно направленных сопел, если скорость истечения v можно считать постоянной по сечению сопел, площадь которых оди-
накова и равна S =0,012 м 2 , а расстояние между их осями L. Рассмотреть два случая: сопла неподвижны и сопла вращаются с угловой скоростью =1,2 1/с.
К задачам 7-33 34 К задачам 7-35 36 К задачам 7-37 38
109
7-39 40. Вода вытекает из резервуара через изогнутую вращающуюся трубку при постоянном напоре Н. Диаметр трубки d=40 мм, выходной радиус r=0,5 м , выходной угол . Коэффициент потерь при течении воды по трубке=0,2. Определить момент действия потока на трубку при равномерном вращении с угловой скоростью =5 1/с. При какой скорости вращения момент действия потока на трубку станет равным нулю?
7-41 42. Из диффузора, входной и выходной диаметры которого D1 =250 мм, D2 =500 мм, вода поступает в бак с постоянным уровнем Н со ско-
ростью v2 v . Определить осевую силу, действующую на диффузор при коэффициенте потерь в =0,25 (по v1 ). При каком вакууме в баке искомая сила будет равна нулю?
7-43 44. |
Предохранительный клапан с седлом диаметром |
d=25 мм про- |
|
пускает при |
избыточном давлении в седле p=3,2 |
МПа |
расход масла |
( 920 кг / м3 ) равный Q, при этом открытие клапана |
S=5 мм. Считая жид- |
||
кость невязкой, определить направление вытекающей из него струи (угол ),
если известно что начальное давление открытия клапана |
p0 , а жесткость его |
||
пружины С =20 Н/мм. |
|
|
|
7-45 46. Предохранительный клапан с седлом диаметром |
d=24 мм про- |
||
пускает при избыточном |
давлении в седле p=3,0 |
МПа |
расход масла |
( 910 кг / м3 ) равный Q, |
при этом открытие клапана |
S=5 мм. Считая жид- |
|
кость невязкой, рассчитать жесткость пружины клапана, если известно, что начальное давление открытия клапана p0 , а струя из клапанной щели должна
вытекать под углом 70о .
К задачам 7-39 40 |
К задачам 7-41 42 |
К задачам 7-43 46 |
110
