Решенные задачи про аэрогидромеханике (4 вариант) (Краснокутский И.Д) / Задача 6

Бормотов. А

гр. 15-КС-1

Вариант 4

Задача 6.4

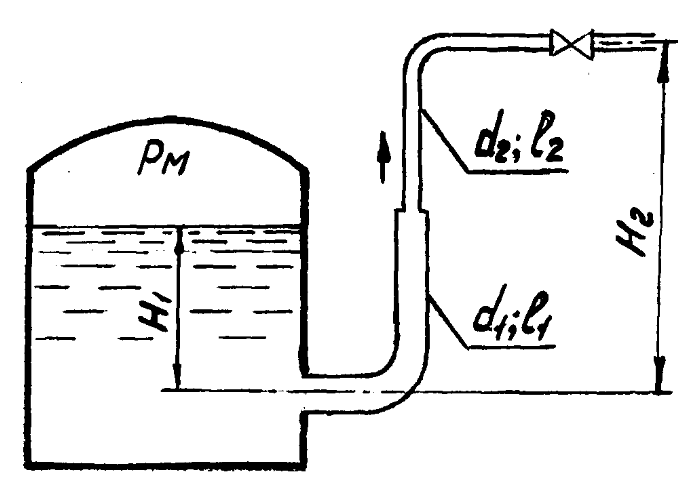
Из резервуара по трубопроводу (d₁, l₁, d₂, l₂) подается вода на высоту H₂=10м. Шероховатость стенок трубопровода ∆=0,20мм. Коэффициент сопротивления для крана принять равным _К, а для поворотов трубопровода - _пов0,40. Определить расход воды через кран, если уровень H₁ воды в резервуаре постоянный, а показание манометра составляет p_м.

Дано:

d₁=0,044 м

l₁=10 м

d₂=0,028 м

l₂=12 м

H₁=1,4 м

H₂=10 м

_К=5

_пов0,40

p_м=150 кПа

ρ_Ж=1000 кг/м³

ν=0,011 Ст=1,1*10^-6 м²/с

Q - ?

Решение:

1)

Внезапное сужение трубы:

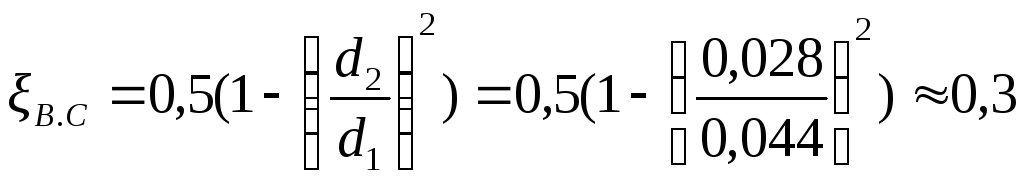
Уравнение Бернулли для сечений 2-2 и 1-1:

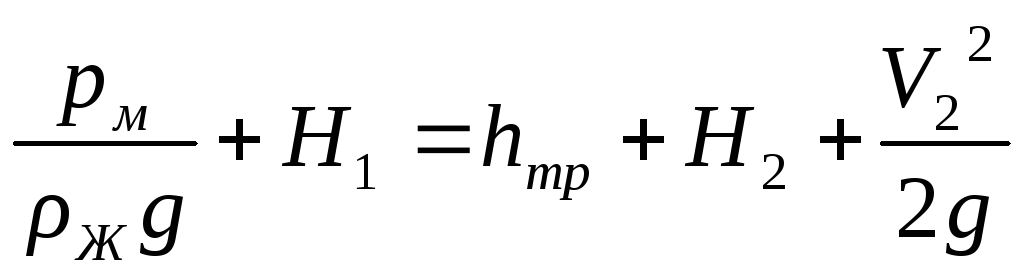
Выражение средней скорости:

Потери на трение находим из формулы:

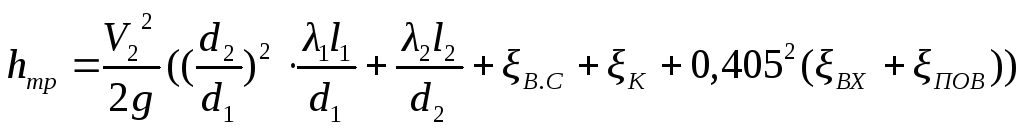
Пусть в 6-м приближении течение соответствует квадратичной зоне. Тогда:

Отсюда:

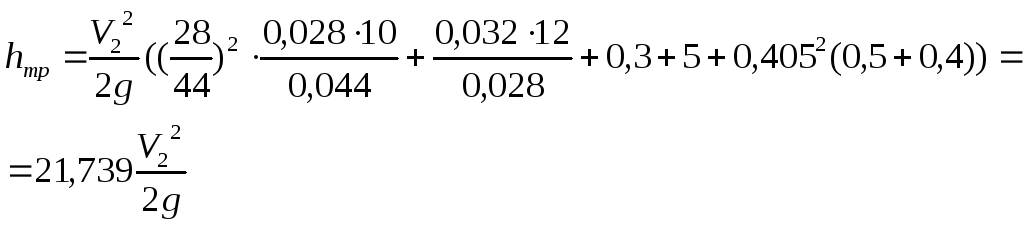
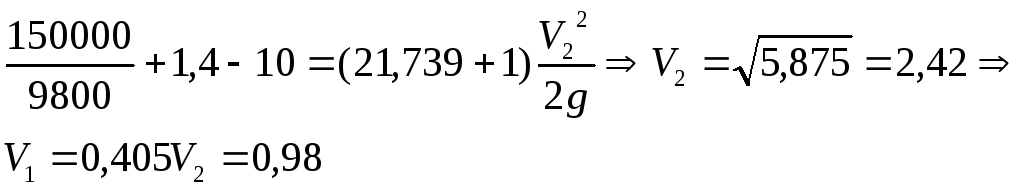
Числа Рейнольдса найдем по формулам:

Рассмотрим 2-ое приближение, используя формулу Альтшуля:

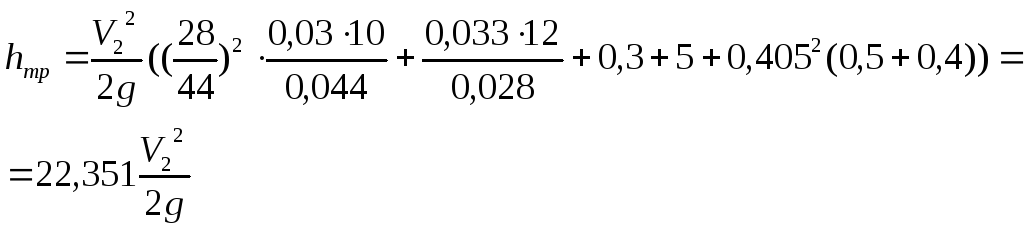
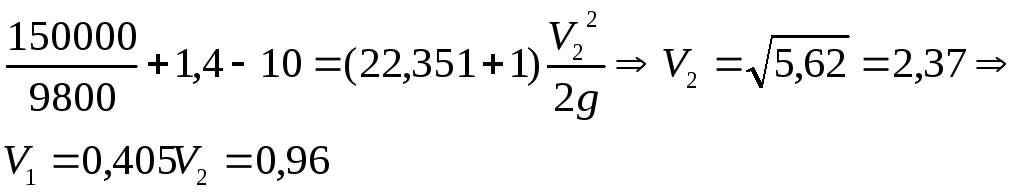
Тогда расход воды:

Ответ: Q=1,45 л/с