
- •Индивидуальное домашнее задание №3 по эконометрике Тема: Множественная линейная регрессия
- •Построим множественную линейную регрессионную модель связи переменных.
- •Таким образом, получено следующее уравнение множественной регрессии:
- •Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их.
- •Коэффициент множественной корреляции:
- •Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
- •С помощью -критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации .
- •С помощью частных -критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора x1 после x2 и фактора x2 после x1
С помощью -критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации .
Оценим надежность уравнения регрессии
в целом и показателя тесноты связи
![]() с помощью
-критерий
Фишера:
с помощью
-критерий
Фишера:
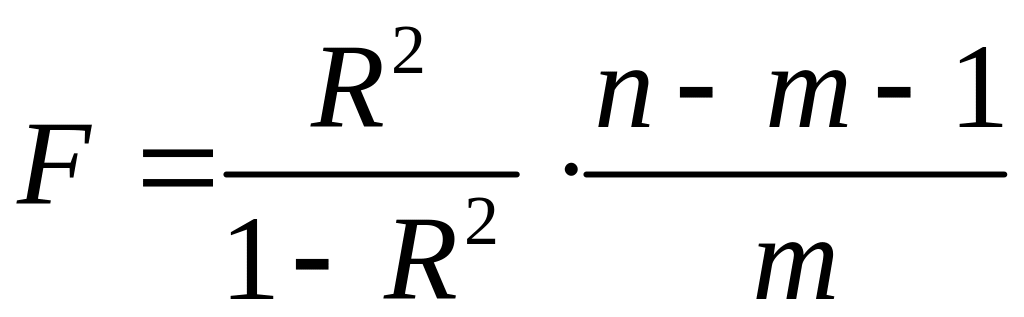 .
.
В нашем случае фактическое значение -критерия Фишера:
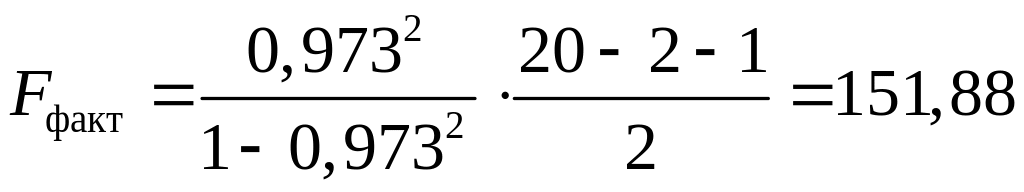 53,21266
53,21266
Получили, что
![]() 4,03 (при n=50), т.е. вероятность
случайно получить такое значение
-критерия
не превышает допустимый уровень
значимости 0,05. Следовательно, полученное
значение не случайно, оно сформировалось
под влиянием существенных факторов.
Подтверждается статистическая значимость
всего уравнения и показателя тесноты
связи
4,03 (при n=50), т.е. вероятность
случайно получить такое значение
-критерия
не превышает допустимый уровень
значимости 0,05. Следовательно, полученное
значение не случайно, оно сформировалось
под влиянием существенных факторов.
Подтверждается статистическая значимость
всего уравнения и показателя тесноты
связи
![]() .
.
С помощью частных -критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора x1 после x2 и фактора x2 после x1
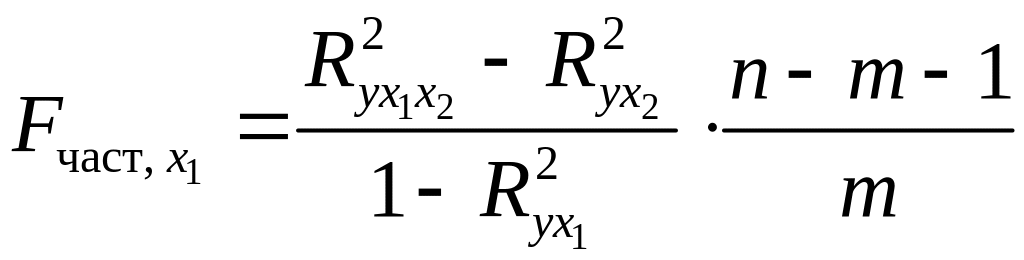 ;
;
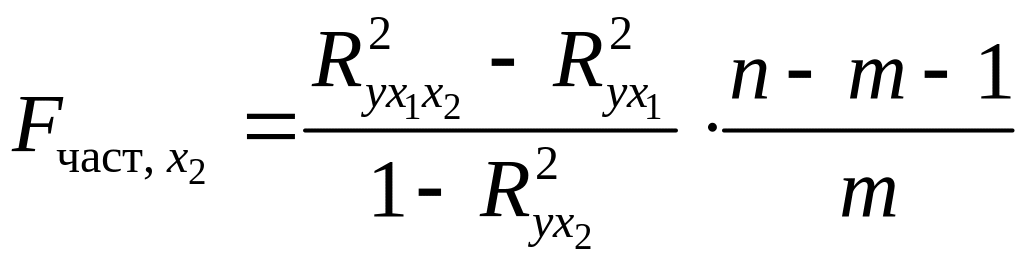 .
.Найдем
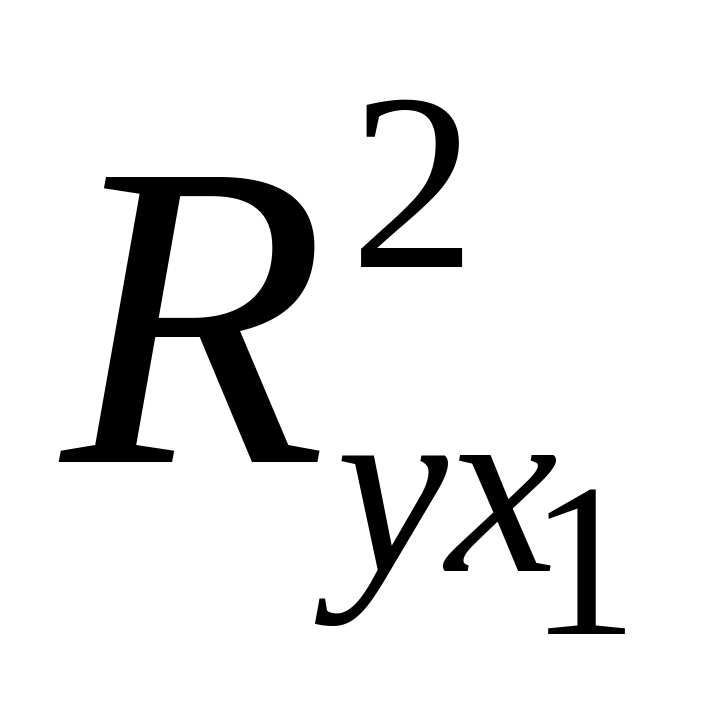 и
и
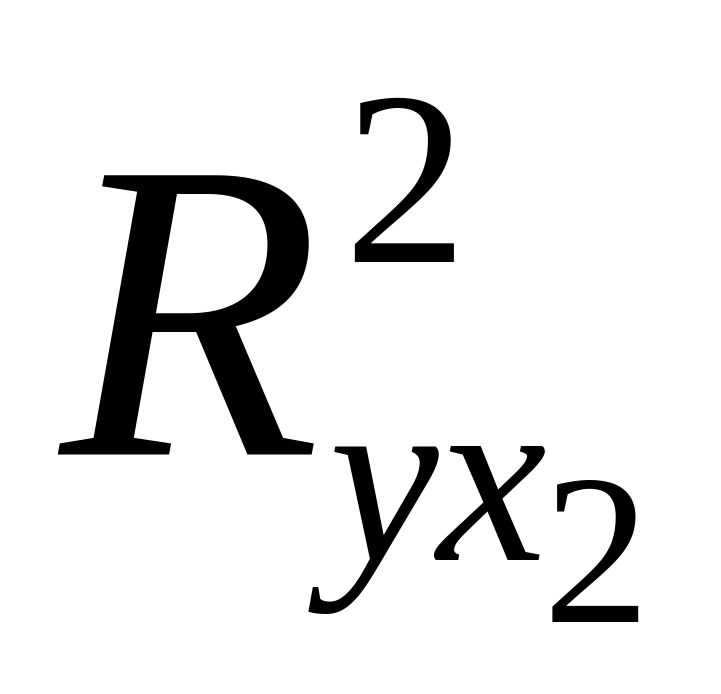 .
.
![]() 0,449836
0,449836
![]() 0,693542
0,693542
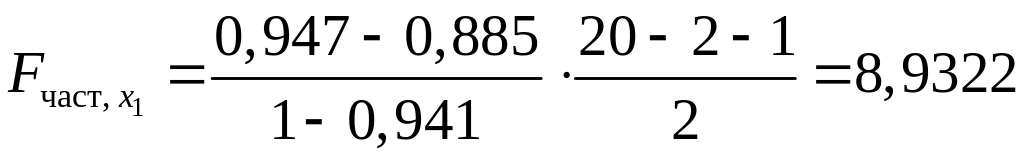 0,005129;
0,005129;
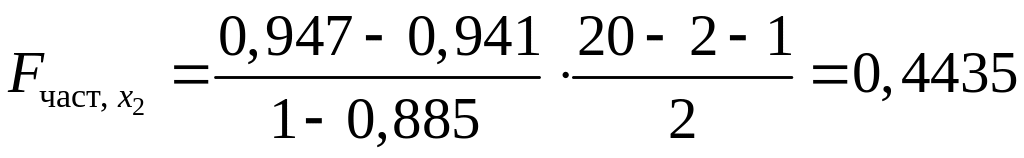 18,69722
18,69722
Получили, что
![]() 4,03.
Следовательно, включение в модель
фактора
после того, как в модель включен фактор
статистически нецелесообразно: прирост
факторной дисперсии за счет дополнительного
признака
оказывается незначительным, несущественным;
фактор
включать в уравнение после фактора
не следует.
4,03.
Следовательно, включение в модель
фактора
после того, как в модель включен фактор
статистически нецелесообразно: прирост
факторной дисперсии за счет дополнительного
признака
оказывается незначительным, несущественным;
фактор
включать в уравнение после фактора
не следует.
Если поменять первоначальный порядок включения факторов в модель и рассмотреть вариант включения после , то результат расчета частного -критерия для будет иным.
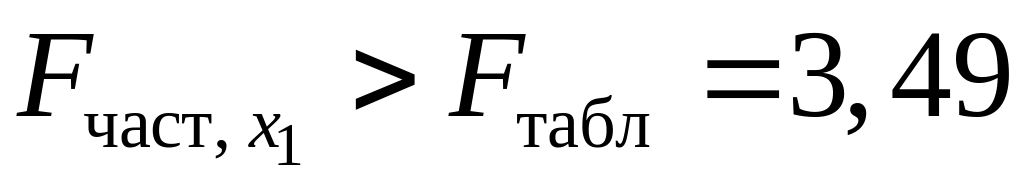 4,03,
т.е. вероятность его случайного
формирования меньше принятого стандарта
4,03,
т.е. вероятность его случайного
формирования меньше принятого стандарта
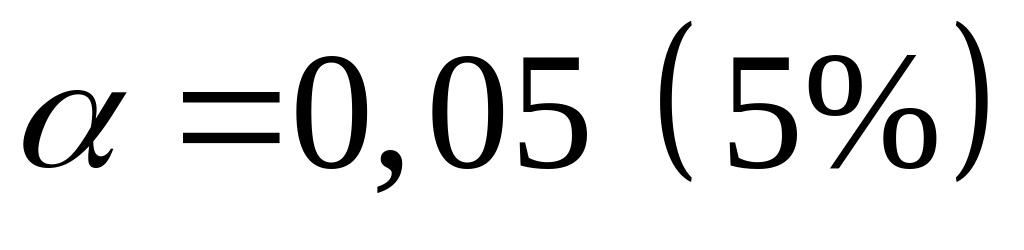 .
Следовательно, значение частного
-критерия
для дополнительно включенного фактора
не случайно, является статистически
значимым, надежным, достоверным. Прирост
факторной дисперсии за счет дополнительного
фактора
является существенным. Фактор
должен присутствовать в уравнении, в
том числе в варианте, когда он дополнительно
включается после фактора
.
.
Следовательно, значение частного
-критерия
для дополнительно включенного фактора
не случайно, является статистически
значимым, надежным, достоверным. Прирост
факторной дисперсии за счет дополнительного
фактора
является существенным. Фактор
должен присутствовать в уравнении, в
том числе в варианте, когда он дополнительно
включается после фактора
.
Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор
Фактор x1 - неинформативный. Если его исключить, то можно ограничиться уравнением парной регрессии
Y = a + b*x2 + E
a=99.24 b=0.22
y = 99.24 + 0.22*x2 +E
0,693662
R2yx2 =0,693542
Если < R2yx2, то фактор исключен верно.
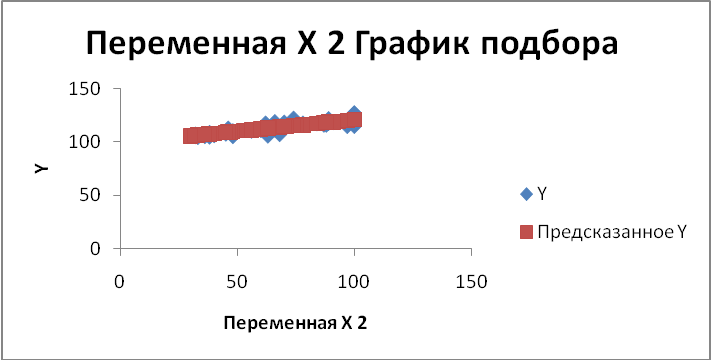
Предполагаем наличие линейной связи между объясняемой переменной y и фактором x2.
Проверить выполнение стандартных предположений регрессионного анализа для полученной модели графическим методом
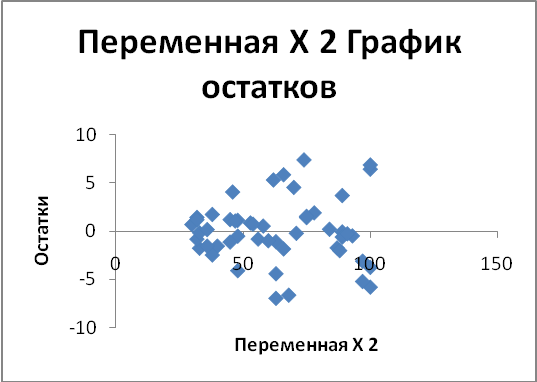
На графике нет выделяющихся наблюдений,
что могло бы указывать на отличие
математического ожидания ошибок от
нуля
![]() ,
либо на неоднородность дисперсии ошибок.
Не наблюдается функциональной зависимости
,
либо на неоднородность дисперсии ошибок.
Не наблюдается функциональной зависимости
![]() от
величины
от
величины
![]() ,
то есть дисперсия ошибок гомоскедастична.
Судя по графику, условие
,
то есть дисперсия ошибок гомоскедастична.
Судя по графику, условие
![]() выполняется, то есть спецификация модели
подобрана правильно.
выполняется, то есть спецификация модели
подобрана правильно.
Таким образом, используемые для построения модели статистические данные соответствуют стандартным предположениям регрессионного анализа.
