Элементы комбинаторики

Научимся подсчитывать число "шансов". О числе шансов говорят, когда возможно несколько результатов какого-либо действия (выбор карты из колоды, подбрасывание кубика или монетки). Формулы комбинаторики позволяют посчитать число способов проделать действие или число его возможных результатов.

Основной принцип комбинаторики заключается в следующем: если первый элемент можно выбрать способами, а второй элемент - способами, то упорядоченную пару элементов можно составить способами.

Урновые схемы. Есть урна (ящик), содержащая пронумерованных шаров. Мы выбираем из урны шаров; результат этого выбора - набор из шаров. Нас интересует, сколькими способами можно выбрать шаров из , т. е. сколько различных результатов возможно.

На этот вопрос нельзя дать однозначный ответ, пока мы не знаем:

1. как организован выбор;

2. что понимать под различными результатами выбора.

Рассмотрим следующие возможные способы выбора.

1. Выбор с возвращением: каждый вынутый шар возвращается в урну, каждый следующий шар выбирается из полной урны. В полученном наборе из номеров шаров могут встречаться одни и те же номера.

2. Выбор без возвращения: вынутые шары в урну не возвращаются, и в полученном наборе не могут встречаться одни и те же номера.

Условимся, какие результаты выбора (какие наборы номеров шаров) мы будем считать различными. Есть ровно две возможности.

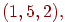
1. Выбор с учетом порядка: два набора номеров шаров считаются различными, если они отличаются составом или порядком номеров. Так, наборы и считаются различными наборами.

2. Выбор без учета порядка: два набора номеров шаров считаются различными, если они отличаются составом. Так, наборы и различны, а наборы и не различаются.

Количество результатов в урновых схемах. Подсчитаем, сколько возможно различных результатов для каждой из четырех схем выбора: с возвращением или без возвращения, и в каждом из этих случаев - с учетом порядка или без учета.

Выбор без возвращения и с учетом порядка

Общее количество различных наборов при выборе элементов из без возвращения и с учетом порядка равняется

Число называется числом размещений из элементов по элементов, а сами результаты выбора - размещениями.

В множестве из элементов возможно ровно P_n= перестановок этих элементов.

Выбор без возвращения и без учета порядка

Общее количество различных наборов при выборе элементов из без возвращения и без учета порядка равняется

Число называется числом сочетаний из элементов по элементов, а сами результаты выбора - сочетаниями.

Выбор с возвращением и с учетом порядка

Общее количество различных наборов при выборе элементов из с возвращением и с учетом порядка равняется

Выбор с возвращением и без учета порядка. Рассмотрим урну с двумя пронумерованными шарами и перечислим результаты выбора двух шариков из этой урны при выборе с возвращением. Если учитывать порядок, то исходов получится четыре:

Если порядок не учитывать, то следует объявить два последних исхода одним и тем же результатом эксперимента. Исходов окажется три:

Видим, что в схеме выбора без учета порядка получилось три различных результата, тогда как при выборе с учетом порядка различных результатов было четыре.

Общее количество различных наборов при выборе элементов из с возвращением и без учета порядка равняется